Seriál 10. ročníku
Celý seriál je také možné nalézt v ročence.
Úlohy
1. Série 10. Ročníku - S. hvězdná velikost
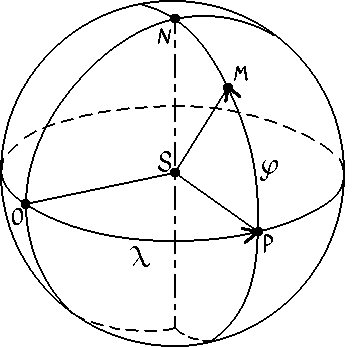
Na procvičení pojmu hvězdné velikosti si vyřešte tyto úlohy:
- Jaká je absolutní magnituda Slunce $M$, je-li jeho zdánlivá magnituda $m=-26,74$?
- Složky dvojhvězdy Castor v souhvězdí Blíženců jsou v dalekohledu jasné $m_{A}=2,0$ a $m_{B}=2,9$. Neozbrojené lidské oko však tyto hvězdy nerozliší. Jak jasná se jeví tato dvojhvězda při pozorovaní pouhým okem?
- V jaké poloze na své dráze se jeví Venuše ze Země nejjasnější? Předpokládejte, že Venuše obíhá kolem Slunce přibližně po kružnici s poloměrem $r=0,7233\;\mathrm{AU}$ a že jasnost v celé viditelné a osvětlené části povrchu Venuše je konstantní. U těch, co neumějí derivovat, se spokojíme s numerickou hodnotou vzdálenosti Venuše od Země; nakreslete si graf závislosti jasnosti Venuše na vzdálenosti a odečtete z něj polohu největší jasnosti.
- Pokuste se odhadnout jasnost Venuše v poloze, kdy je na obloze od Slunce úhlově nejdál. Albedo Venuše (tj. poměr odražené ku dopadající intenzitě záření) je $0,76$ a její poloměr $R_{V}=6052\;\mathrm{km}$. Předpokládejte, že záření odražené od Venuše se rovnoměrně rozptýlí do celého poloprostoru a že jasnost každého světlého místa viditelného povrchu bude, jako by Slunce bylo právě nad ním.
- Určete, v jaké největší a nejmenší výšce nad obzorem se v naší zeměpisné šířce nachazí Slunce během roku. Rovina ekliptiky s rovinou zemského rovníku svírá úhel $23,5$ stupňů.
2. Série 10. Ročníku - S. oběžná dráha Země kolem Slunce
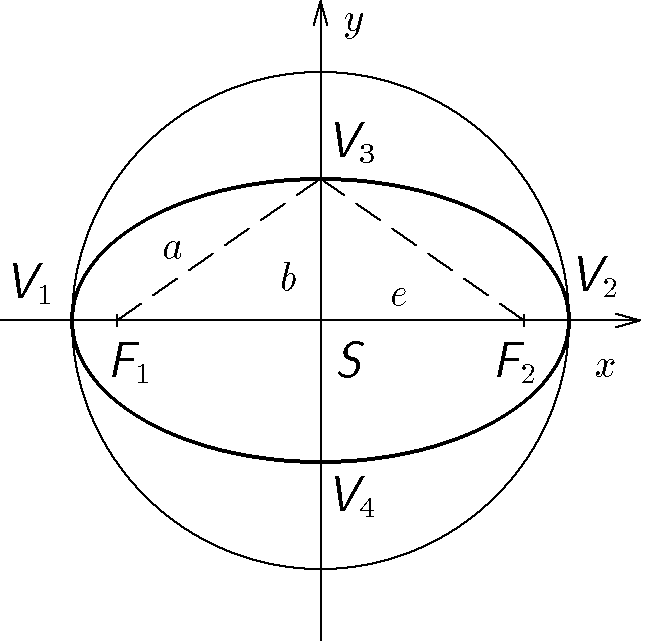
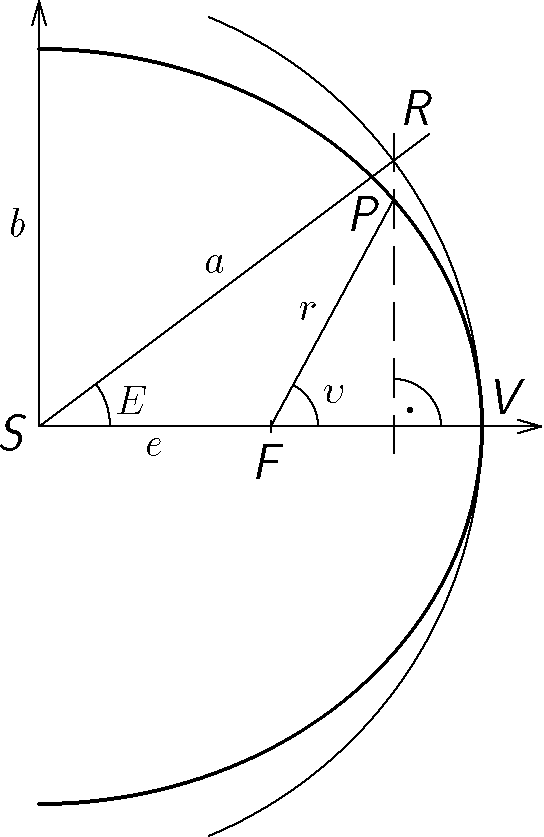
Určete pravou anomálii a vzdálenost Země od Slunce po $1/4$ oběžné doby Země kolem Slunce od průchodu Země periheliem. Velká poloosa je $a=1\;\mathrm{AU}$ a excentricita $e=0,0167$.
3. Série 10. Ročníku - S. Venuše
Spočtěte ekliptikální a rovníkové souřadnice Venuše pro 24. 8. 1988 v $0^{h}UT$ (světový čas). Pro tento den určete vzdálenost Venuše od Země a máte-li doma nějakou hvězdnou mapu, určete také souhvězdí, ve kterém se Venuše nachází. Elementy drah Venuše a Země jsou:
| $a_{V}=0,72333\; \textrm{AU}$ | $e_{V}=0,00679$ | $i_{V}=3,3949^{o}$ | $\Omega_{V}=76,7112^{o}$ | $\omega_{V}=55,0804^{o}$ |
| $a_{Z}=1,00000\; \textrm{AU}$ | $e_{Z}=0,01673$ | $i_{Z}=0,0014^{o}$ | $\Omega_{Z}=352,2647^{o}$ | $\omega_{Z}=110,6756^{o}$ |
Oběžná doba Země kolem Slunce je $T_{Z} = 365,2571\; \textrm{dne}$. Údaj o okamžiku průchodu planet periheliem je nahrazen zadáním středních anomálií Venuše $M_{0}^{V}$ a Země $M_{0}^{Z}$ pro 18. 7. 1988 v $0^{h} UT$:
$$M_{0}^{V}=186,0712^{o}$$ $$M_{0}^{Z}=193,2434^{o}$$
Při řešení nepoužívejte žádné vztahy vyčtené z knih o astronomii.
4. Série 10. Ročníku - S. Slunce a meteoroidy
Ověřte hypotézu, že zdrojem energie Slunce jsou meteoroidy dopadající na jeho povrch. Určete, kolik meteoroidů (jejich hmotnost) by muselo dopadnout na Slunce za 1 rok, aby se energeticky pokryl zářivý výkon Slunce $L=3,83\cdot 10^{26}\, \jd{W}$. Předpokládejte, že se vyzáří veškerá kinetická energie meteoroidů (ve skutečnosti se část této energie spotřebuje na ohřev Slunce a na změnu celkové potenciální energie Slunce). Poloměr Slunce je $R=6,96\cdot 10^{8}\, \jd{m}$, hmotnost $1,99\cdot 10^{30}\, \jd{kg}$. Určete, o kolik by se za rok změnila velká poloosa a doba oběhu Země díky nárůstu hmotnosti Slunce. Předpokládejte, že se hmotnost Slunce mění skokově a že před touto změnou obíhala Země kolem Slunce po kružnici o poloměru $a=1\;\mathrm{AU}=1,496\cdot 10^{11}\, \jd{m}$ s dobou oběhu $T = 1\, \jd{rok}$. Při výpočtu použijte přibližný vztah $(1 + x)^{k}=1+kx$, který platí pro $k$ reálné. Dnes je známa astronomická jednotka s přesností na 2 metry. Bylo by možné tuto změnu naměřit?
5. Série 10. Ročníku - S. hvězdy
- Zkuste jednoduše zdůvodnit, proč je gravitační síla působící na těleso o hmotnosti $m$ ve vzdálenosti $r$ od středu izotropní koule o poloměru $R>r$ daná pouze hmotou $M(r)$ obsaženou v kouli o poloměru $r$ a proč je rovna $F_{g}=κmM(r)/r^{2}$, tj. jakoby byla celá hmota $M(r)$ soustředěna v centru.
- Existuje jistá skupina tzv. polytropních modelů hvězd, které jsme již schopni počítat. V těchto modelech se předpokládá závislost tlaku $p$ na hustotě $ρ$ ve tvaru $p=Cρ^{γ}$
(tzv. rovnice polytropy). Speciálním případem polytropy je adiabata (pro $γ=4/3)$, izoterma (pro $γ=1)$ a izobara (pro $γ=0)$. Pro funkce $p(r)$ a $ρ(r)$ tak máme, spolu s rovnicí hydrostatické rovnováhy, rovnice dvě a můžeme z našich úvah vyloučit teplotu. Odhadněte, stejným způsobem jako v seriálu, vztah mezi hmotností hvězdy $M$ a jejím poloměrem $R$. Určete, pro které hodnoty parametru polytropy $γ$ je hvězda stabilní.
6. Série 10. Ročníku - S. hmotnost hvězd a tak
- Určete, jak závisí doba života hvězdy na její hmotnosti.
- Vztah z teoretické části seriálu nám dovoluje určovat vzdálenosti dvojhvězd a hmotnosti jejich složek. Jako příklad může sloužit dvojhvězda 70 Oph. Měřením bylo zjištěno, že oběžná doba složek dvojhvězdy je $T=87,85\;\mathrm{roku}$, velká poloosa jejich dráhy má na obloze úhlovou délku $a=4,551''$. Zdánlivé magnitudy složek jsou $m_{A}=3,93$, $m_{B}=5,29$. Z těchto údajů vypočtěte vzdálenost systému a hmotnosti jednotlivých složek.