Seriál 18. ročníku
Celý seriál je také možné nalézt v ročence.
Úlohy
1. Série 18. Ročníku - S. kinematika hmotného bodu
Poloha hmotného bodu v závislosti na čase v kartézské souřadnicové soustavě je popsána polohovým vektorem $r(t) =(R \cos\(\omega t\),R \sin\(\omega t\))$. Určete, jak závisí na čase vektory $v(t)$ a $a(t)$. Vypočítejte také tečnou, normálovou a binormálovou složku zrychlení.
- Kolo poloměru $R$ se valí bez prokluzování po přímé dráze rychlostí $v$. S kolem je pevně spojen bod ve vzdálenosti $r$ od středu. Určete jeho pohyb a rychlost jako funkce času v soustavě spojené se Zemí. Může být jeho rychlost v určitém okamžiku nulová?
Zadali autoři seriálu Honza Prachař a Jarda Trnka.
2. Série 18. Ročníku - S. Newtonovy pohybové rovnice
Napište a řešte pohybové rovnice hmotného bodu v tíhovém poli Země. Souřadnicovou soustavu orientujte tak, že osy $x$ a $y$ jsou vodorovné a osa $z$ míří vzhůru. Počáteční poloha hmotného bodu je $r_{0} = (0,0,h)$, počáteční rychlost je $v_{0} =(v_{0}\cosα,0,v_{0}\sinα)$.
Muž s puškou sedí v křesle, které se otáčí kolem svislé osy s frekvencí $f = 1\, \jd{Hz}$. Spolu s křeslem se otáčí terč, který je k němu pevně upevněn. V jistém okamžiku muž vystřelí kulku rychlostí $v = 300\, \jd{km \cdot h^{-1}}$ směrem od osy otáčení přesně do středu terče. V jakém místě prorazí kulka terč? Řešte jak z pohledu neinerciální, tak z pohledu inerciální vztažné soustavy. Vzdálenost hlavně od středu terče je $l=3\, \jd{m}$, odpor vzduchu zanedbejte.
Vyjádřete závislost rychlosti hmotného bodu na poloze v gravitačním poli Slunce.
Zadal Honza Prachař.
3. Série 18. Ročníku - S. Lagrangeovy rovnice 1. druhu
Mějme hmotný bod zavěšený na nehmotném a nepružném vlákně.
- Zaveďte kartézskou souřadnicovou soustavu a v ní napište vazebnou podmínku pro hmotný bod.
- Napište Lagrangeovy rovnice 1. druhu pro hmotný bod z předchozí části. Ukažte, že jsou ekvivalentní s rovnicí matematického kyvadla $\frac{\rm{d}^{2} \varphi}{\rm{d}t^{2}} + \frac{g}{l} \sin \varphi = 0$, kde $\varphi$ je úhlová výchylka z rovnovážné polohy.
- Malé těleso je v klidu na vrcholu polokoule a začne klouzat dolů. Pomocí Lagrangeových rovnic 1. druhu určete, v jaké výšce se těleso odlepí od polokoule. ( Nápověda: Těleso se odlepí v okamžiku, kdy $\lambda = 0$.)
Úlohu zadali autoři seriálu Honza Prachař a Jarda Trnka.
4. Série 18. Ročníku - S. Lagrangeovy rovnice 2. druhu
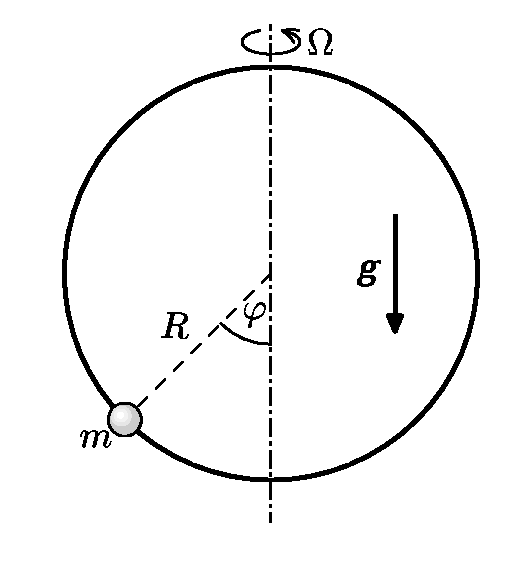
Malý korálek o hmotnosti $m$ klouže bez tření na drátu ve tvaru kruhové smyčky poloměru $R$, smyčka se otáčí konstantní úhlovou rychlostí $Ω$ kolem svislé osy (viz obrázek).
- Vhodně zvolte zobecněnou souřadnici a sestrojte Lagrangeovu funkci problému.
- Sestavte Lagrangeovu rovnici 2. druhu, která popisuje pohyb korálku.
- Rozhodněte, kdy je rovnovážná poloha v nejnižší poloze smyčky stabilní a kdy je labilní v závislosti na $Ω$. Pro $Ω$, kdy je tato poloha stabilní, vypočítejte periodu kmitů korálku kolem této polohy.
- Za bonusové body nalezněte další rovnovážné polohy a diskutujte, zda jsou stabilní, nebo labilní. Pokud jsou stabilní, určete periodu kmitů kuličky kolem těchto rovnovážných poloh.
Navrhli autoři seriálu Jarda Trnka a Honza Prachař.
5. Série 18. Ročníku - S. Merkur, jáma a kyvadlo
V následujících úlohách ověříme vaši znalost všech dosud probraných kapitol mechaniky, tj. Newtonova formalismu, D'Alembertova principu a Lagrangeova formalismu.
- Představte si planetu Merkur obíhající kolem Slunce. Jak známo, jeho eliptická trajektorie se stáčí (posouvá se poloha perihélia), což nemůže být způsobeno gravitační silou $F=κ(mMr)⁄r^{3}$. Dokažte, že když k této síle přidáme dodatečnou centrální sílu $F=C(r)⁄r^{4}$, kde $C$ je vhodná konstanta, celá trajektorie (elipsa) se bude otáčet konstantní úhlovou rychlostí (čili existuje vztažná soustava otáčející se konstantní úhlovou rychlostí taková, že trajektorie v ní bude elipsa). Znáte-li tuto úhlovou rychlost $Ω$, určete konstantu $C$. Stačí takováto oprava k záchraně Newtonovy teorie gravitace?
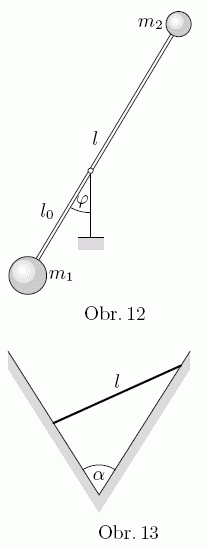
- Určete rovnovážné polohy homogenní tyčky délky $l$ opřené o vnitřní stěny jamky ve tvaru písmene „V“ (viz obr. 12) v závislosti na vrcholovém úhlu jamky $α$.
- Pomocí Lagrangeových rovnic vypočítejte periodu malých kmitů dvojzvratného kyvadla na obrázku 13. Závaží na koncích nehmotné tyčky délky $l$ mají hmotnosti $m_{1}$ a $m_{2}$, vzdálenost bodu závěsu od závaží o hmotnosti $m_{1}$ je $l_{0}$.
Na úlohu (1) narazil Matouš v jedné pěkné ruské knize; (2) a (3) zadal Honza Prachař a Jarda Trnka.
6. Série 18. Ročníku - S. Hamiltonův formalismus
Langrangián částice v elektromagnetickém poli je $L=\frac{1}{2}mv-qφ+q v\cdot A=\frac{1}{2}m\cdot \sum_{i=1}^{3}v_{i}-qφ+q\cdot \sum_{i=1}^{3}v_{i}A_{i}$,
kde $φ$ je elektrický potenciál a $A$ magnetický vektorový potenciál.
- Určete zobecněné hybnosti částice $p_{i}$ příslušející rychlostem $v_{i}$.
- Napište Hamiltonovu funkci (v proměnných ($x_{i}$, p$_{i})!)$.
- Řešte Hamiltonovy rovnice, je-li $A=0$ a $φ=-Ex_{1}$.
Zadal Honza Prachař.