Seriál 22. ročníku
Celý seriál je také možné nalézt v ročence.
Úlohy
1. Série 22. Ročníku - S. princip ekvivalence
- Jaké by musely nastat podmínky, aby Galileův pokus nevyšel? Šikmá věž v Pise je vysoká $h =55\, \jd{m}$, předpokládejte, že obě koule mají poloměr $R = 8\, \jd{cm}$ a že jedna koule je vyrobena z olova o hustotě $ρ = 11300\, \jd{kg\cdot m^{ - 3}}$. Jakou hustotu by musela mít druhá koule, aby rozdíl v časech dopadu obou koulí byl větší než $ΔT = 0,3\, \jd{s}$?
- S jakou přesností ověřuje původní Eötvösovo měření rovnosti poměru gravitační a setrvačné hmotnosti pro neutrony a protony, pokud ve dřevě tvoří neutrony 50 procent hmotnosti, zatímco v platině 60 procent hmotnosti? Zanedbejte hmotnost elektronů a vazebné energie.
- Ověřte užívaný předpoklad o tom, že v Budapešti je $g_{s}$ v porovnání s $g$ zanedbatelné.
Zadali autoři seriálu Jakub Benda a Pavel Motloch.
2. Série 22. Ročníku - S. Young a vlnová povaha světla
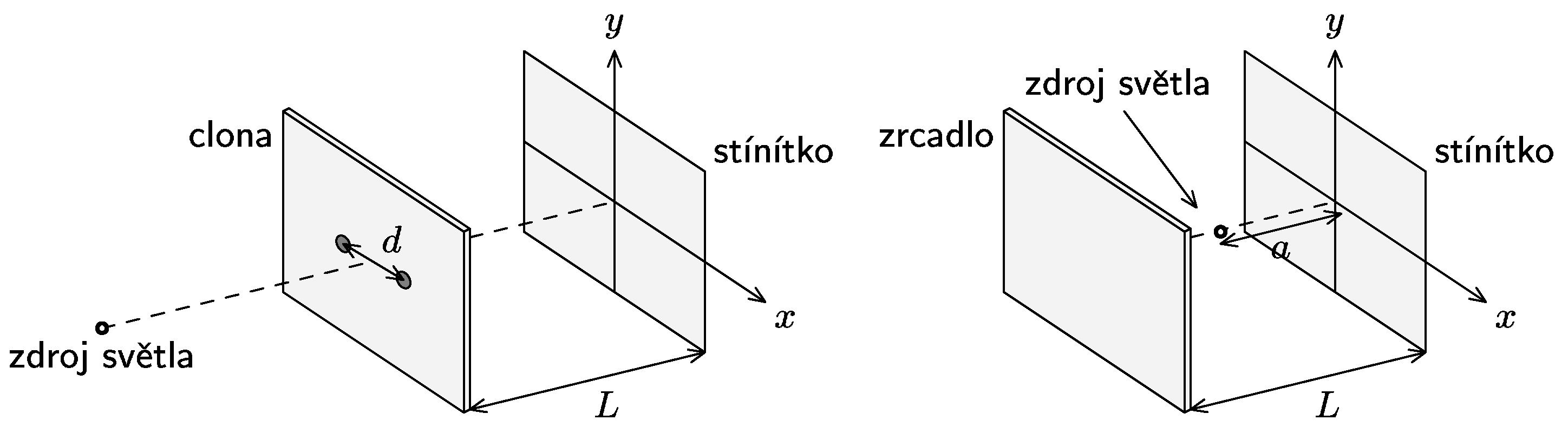
K zadání úlohy
- Jaký tvar interferenčních proužků na stínítku byste očekávali v následujících dvou sestavách? Najděte rovnice křivek maximální intenzity a zkuste jich několik načrtnout.
- Ukažte, jak by dopadl Youngův experiment, jestliže by se světlo chovalo podle Newtonových představ (tzn. difrakce ano, interference ne). nezapomeňte vzít v úvahu různý úhel dopadu světla na různá místa stínítka.
- Užitím vyloženého kvantověmechanického popisu určete rozložení intenzity, jaké by dostal Jöhnsson při použití čtyřštěrbiny (tedy čtyř úzkých rovnoběžných otvorů rozmístěných ve vzdálenostech $b$ od sebe). Načrtněte reprezentativní úsek grafu a okomentujte přednosti většího počtu otvorů.
Autoři seriálu
3. Série 22. Ročníku - S. céčková
- Představte si, že vezmete dostatečně silný laser, vyzařující světlo vlnové délky $400\, \jd{nm}$, a posvítíte s ním na Měsíc. Od jeho povrchu se vyzářené světlo odrazí a vrátí se zpět. Předpokládáme-li, že laser vyzařuje skrze kruhový otvor průměru $1\, \jd{cm}$, jaký bude na zemském povrchu průměr paprsku navracejícího se po odrazu zpět? Poradíme vám, že to bude o poznání více, než $1\, \jd{cm}$.
- V této úloze předpokládejte, že éter skutečně existuje a předpovězte, jak by to dopadlo, kdyby Michelson prováděl svá měření jiným způsobem: Jedno rameno by nechal dlouhé $5$ metrů, zatímco druhé by bylo dlouhé $10\, \jd{m}$. Takto připravená aparatura by vytvořila nějaký interferenční obrazec. Poté by Michelson celou soustavou otočil o $90^{\circ}$, takže by si obě ramena vyměnila místa. V průběhu tohoto otáčení by docházelo k posunům interferenčních proužků. (Představte si rotující dvojštěrbinu.) Jak by se v uvedené aparatuře posunuly interferenční proužky při naznačené rotaci? Jak dlouhé by muselo být delší rameno, aby se interferenční proužky vyměnily, tedy aby se rotací maxima posunuly na minima?
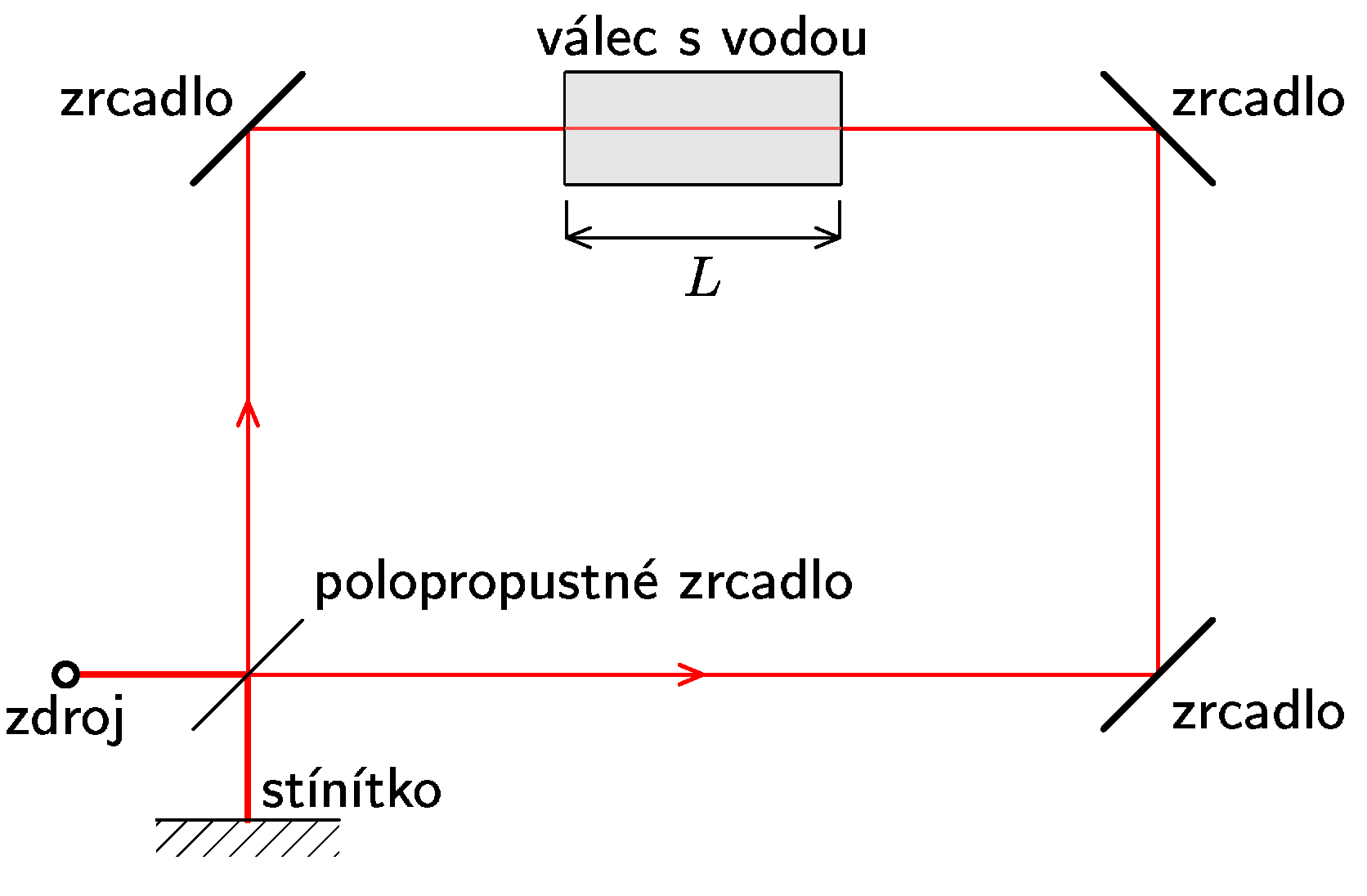
- V následující úloze předpokládejte, že éter existuje a že těleso pohybující se v éteru jej úplně strhuje, takže relativní rychlost tělesa vůči éteru je nulová. Jaký fázový posun by poté vznikl mezi dvěma paprsky v soustavě, naznačené na obrázku? Světlo ze zdroje se na polopropustném zrcadle rozdělí na dva svazky a pokračuje po dokonale obdélníkové dráze zpět na polopropustné zrcadlo, kde vystupuje na stínítko, na kterém sledujeme interferenční proužky. Po cestě jsou oba paprsky třikrát odraženy na zrcadle a procházejí válcem délky $L$, naplněným vodou. Celá soustava kromě válce s vodou (ten je vůči éteru v klidu, nezapomeňte) se vůči éteru pohybuje rychlostí $v$ směrem vpravo.
Zadali autoři seriálu.
4. Série 22. Ročníku - S. Foucaultovo kyvadlo a rotace Země
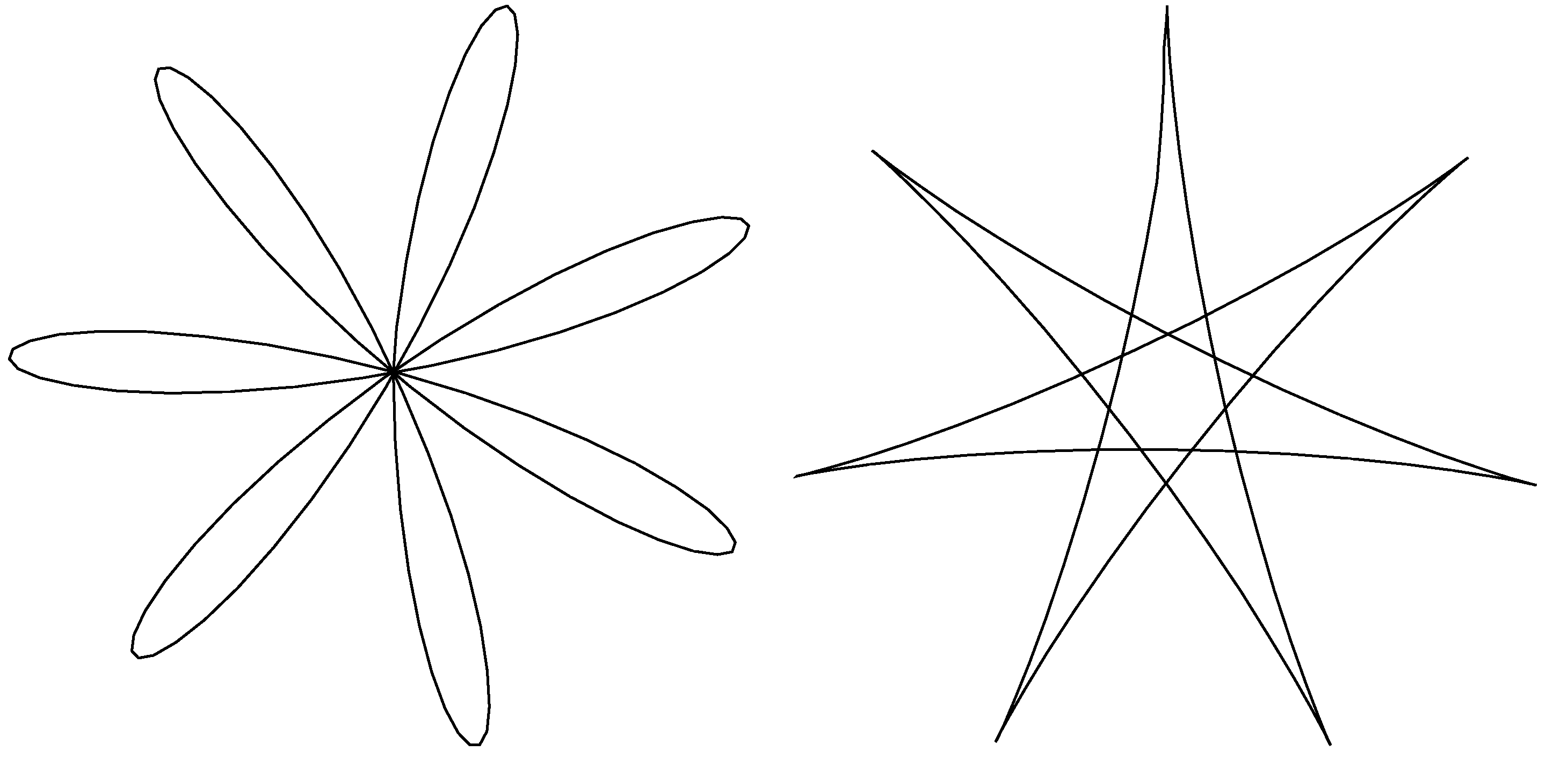
- Foucaultovo kyvadlo do písku nakreslilo při dvou různých demonstracích dva odlišné obrazce, oba jsou na obrázku. Rozhodněte, co způsobilo jiný tvar a také jak dlouhé by muselo být kyvadlo, aby tyto obrazce mohly na podlaze pařížské katedrály vzniknout. Kolikacípé jsou hvězdy/květy ve skutečnosti?
- Jaký tvar bude mít hladina v kbelíku s vodou, který klidně stojí na rovném stole?
- Ukažte, že vztah
$$δf=f_{+}-f_{-}=\frac{4ωS}{λ_{0} P}$$ pro frekvenční rozdíl (frekvenci rázů) dvou protiběžných paprsků v laserovém gyroskopu platí pro jeho libovolný rovinný tvar – tedy nejen kruhový.
K procvičení probrané látky zadali autoři seriálu.
5. Série 22. Ročníku - S. hrátky s elektrony
- Druhým způsobem, kterým měřil J. J. Thomson velikost měrného náboje elektronu, je právě studium vychylování katodového záření elektrickým polem. Uvažujte aparaturu podle obrázku. Jak závisí odchylka paprsku, zaznamenaná na stínítku vpravo, na přiloženém napětí, rychlosti „corpuscules“ a geometrických vlastnostech aparatury?
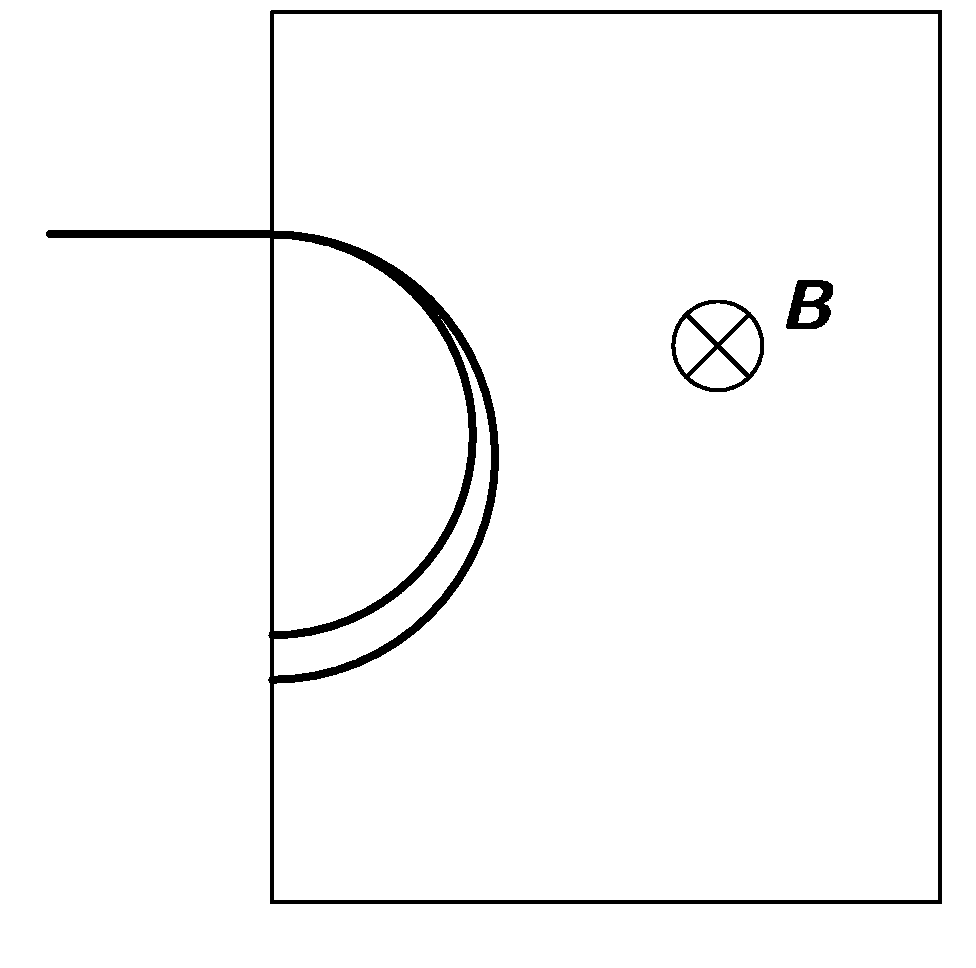
- Jedním z problémů, se kterými se J. J. Thomson potýkal při stanovování měrného náboje elektronů, byl následující: Po vstupu paprsku katodového záření do magnetického pole se paprsek rozšířil do tvaru jakéhosi vějíře (viz obrázek). Tento rozptyl paprsku činí určování poloměru kružnice, kterou katodové záření vytvoří, značně nepřesné (Thomson hovořil o 20 %). Čím můžeme tento rozptyl vysvětlit? Pokud uvedete, jakým způsobem by bylo možno tuto nepřesnost zmenšit, vysloužíte si bonusový bod.
- Zpracováním dat z tabulky určete velikost náboje elektronu v případě, že by olej měl hustotu $920\, \jd{kg\cdot m^{ - 3}}$, vzduch hustotu $1,2\, \jd{kg\cdot m^{ - 3}}$ a viskozitu $17,1 \cdot 10^{-7}\, \jd{Pa\cdot s}$. Užívali jsme elektrické pole o intenzitě $250\, \jd{kV\cdot m^{ - 1}}$.
Zadali Pavel M. a Jakub B.
6. Série 22. Ročníku - S. atomové modely a Rutherfordův experiment
- Rozhodněte, zda stabilita (popř. rozměr) saturnského atomového modelu závisí na atomovém čísle $Z$.
- Upravte vzorec (12) pro pravděpodobnost rozptylu $α$-částice pod velkým úhlem $φ$ tak, abyste dostali praktičtější vztah pro pravděpodobnost dopadu na jednotku plochy scintilátoru, a uvažte, jak byste ho využili k určení materiálu ostřelovaného vzorku. Dále odhadněte, jak by se vzorec změnil, pokud bychom neuvažovali centrální náboj $Ze$ nýbrž $Z$ rozptýlených elementárních nábojů $e$ jako třeba v Lenardově modelu.
- V roce 1896 objevil astronom E. C. Pickering ve světle hvězdy $ζ$ Puppis čáry, které splňovaly vztah (7) pro $n=2$ a $m=2,\!5$; $3$; $3,\!5$; $4$; $4,\!5$; …, tedy i pro polocelá čísla! Vysvětlete tuto zdánlivou nesrovnalost s Bohrovým modelem.
- Bonus: Najděte závislost analogickou rovnici (11) pro Thompsonův pudinkový model a okomentujte rozdíly. Nebo zkuste (11) upravit tak, aby zahrnovala působení jader všech atomů v tenké fólii. Zkrátka si trochu vyhrajte.
Na rozloučenou od autorů seriálu.