Grafické zpracování dat pomocí programu GNUPLOT

Více informací o práci s Gnuplotem můžete získat v tomto stručném návodu.

Před zpracováním již víme a máme:

  1. Definovaný problém a teoretické předpoklady, např. Pepíček střílí prakem do výšky na zemském povrchu. Teorie: Newtonova mechanika, rovnoměrně zrychlený pohyb popsaný kvadratickou závislostí výše ($s_2 = g/2 = 4,90\,\mathrm{m\cdot s^{-2}}$); teorie pružnosti. Předpoklady: Ideální pružina bez disipace energie. (tj. platí ZZE $1/2 mA^2 = 1/2 kR^2$.) Zanedbáváme odpor vzduchu, rotaci Země. Úkol: Stanovit rychlost projektilu $A$ ihned po vystřelení a spočítat tuhost gumy praku $k$.
  2. Dostatečný počet experimentálních bodů v dostatečně velkém intervalu, např. deset výšek $s(t)$ projektilu nad zemí v daném čase (změřených stejným způsobem).
  3. Máme rozmyšlen teoretický základ umožňující využít fitování modelovou funkcí. Tzn. deset hodnot $s(t)$ chceme v souladu s teorií a předpoklady nejlépe vystihnout modelovou funkcí

$$ s(t) = -\frac{g}{2} t^2 + \sqrt{\frac{kR^2}{m}} t + s_0 = -4,90 t^2 + At + s_0\,, $$

kde parametry $A$ a $s_0$ chceme určit fitováním i s chybou fitu! Počáteční polohu nepotřebujeme znát, ale musíme ji do modelové funkce zahrnout, aby fit dal správný výsledek $A$ (podobně je někdy třeba zahrnout pozadí). Srovnáním stran rovnic je pak již jednoduché vyjádřit a vypočítat hledanou tuhost gumy $k$, známe-li hmotnost projektilu $m$ a max. natažení gumy z rovnovážné polohy $R$, tzn. $k = A^2 m/R^2$. Nezapomeňme, že výsledek fitu $A$ musíme napsat se správnou jednotkou, např. měříme-li polohu v metrech a čas v sekundách, pak $[A] = \mathrm{m\cdot s^{-1}}$ a $[k] = \mathrm{kg\cdot s^{-2}} = \mathrm{N\cdot m^{-1}}$.

Při použití programu GNUPLOT ke zpracování musíme naměřené hodnoty uložit v souboru se jménem např. mereni1.txt a s pevnou strukturou, např. 

# č. měření, čas [s], výška [m], chyba měření [m]
# ... legendu a komentář za znakem # gnuplot ignoruje
# číselné hodnoty lze oddělit libovolným počtem mezer či tabulátorem,
# čárka jako desetinný oddělovač je nepřípustná
1	1	17	1
2	2	21	1
3	3	17	1
4	4	3	0.5

Po spuštění gnuplotu uplatníme alespoň následující příkazy:

Prvním příkazem nastavíme pracovní adresář, kde se má hledat soubor s naměřenými hodnotami mereni1.txt. Druhým příkazem definujeme vhodnou modelovou závislost, kterou následným příkazem fitujeme naměřené hodnoty, přičemž nezávislá proměnná $x$ se má načítat ze druhého sloupce a závislá proměnná $s(x)$ ze třetího sloupce. Poslední příkazy zobrazí optimální teoretickou závislost a naměřené hodnoty do společného grafu, kde ihned můžeme zhodnotit správnost fitu, příp. stejný příkaz fit opakovat (někdy se tím parametry A a s0 dále zpřesní) atd.

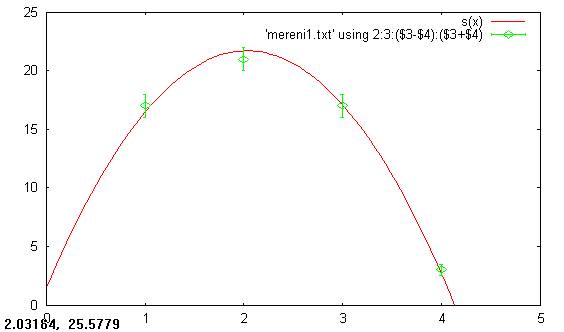
Na obrazovce (terminálu gnuplotu) se nám právě vypsaly poslední hodnoty hledaných parametrů včetně chyby fitu. Pro nalezenou hodnotu $A = (20,0\pm 0,3)\,\mathrm{m/s}$ v našem příkladu spočteme tuhost $k$, na níž se zde ptáme. Dále vidíme, že Pepíček držel prak asi $(1,5\pm 0,8)\,\mathrm{m}$ nad zemí a potřebovali jsme více pokusů na zobrazení pěkného grafu (zde ovšem bez popisků).

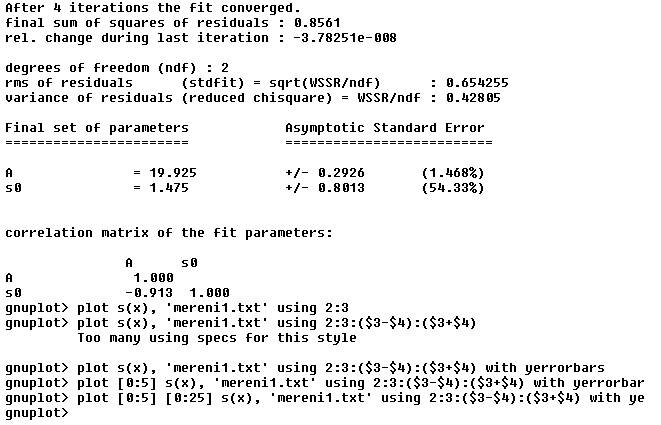
Další užitečné informace, nastavení popisků grafů, znázornění chyb měření a export grafů najdete ve stručném návodu s dalšími příklady a příkazy. Práci v gnuplotu si vyzkoušejte v nejbližším volném čase! Upozorňujeme, že malá a velká písmena nejsou v gnuplotu záměnná!

Automatizace zpracování měření pomocí gnuplotu

Představte si, že v rámci nějakého projektu musíte několikrát opakovat a zpracovávat určité měření, vždy s jedinečným hledaným výsledkem. (Např. Pepíček chce provádět měření několikrát do roka, aby zjistil, jak guma v jeho praku slábne.) Let projektilu, tzn. naměřenou závislost s(t) tedy uložíte každou zvlášť nejlépe v souboru stejného jména, ale v různých adresářích, kam do každého můžete snadno přikopírovat dávkový soubor obsahující příkaz

c:\gnuplot\bin\wgnuplot.exe c:\MUJ_PRAK\zpracuj.gp

zároveň se správnou cestou k modulu gnuplotu a k vašemu skriptu pojmenovanému zpracuj.gp. Ten bude obsahovat sérii vhodných příkazů jako výše, případně dalších přímých výpočtů, jejichž výsledkem je nalezení hledaných hodnot (parametrů). Jestliže byste v terminálu gnuplotu ručně zadávali stále stejnou posloupnost příkazů (mohou-li parametry a jména souborů zůstat stejná), můžete si zjednodušit práci a napsat danou posloupnost jen jednou do skriptu a ten pak postupně spouštět gnuplotem – výsledek bude stejný. Užitečné příkazy jsou shrnuty ve stručném návodu; k úspěšnému využívání skriptů je třeba programátorská zručnost, důvtip a zpočátku trpělivost při zkoušení. Odměnou je zajímavé efektivní využití počítače ke zjednodušení práce. Účastníci soustředění dostanou možnost vyzkoušet si automatizované zpracování v rámci experimentálního odpoledne. Pro čtenáře tohoto úvodu jsme připravili malý příklad (s jiným problémem) pro inspiraci – stáhněte si a rozbalte soubor, spusťte oba *.bat soubory, čímž se vytvoří další soubory v adresáři, a všechny soubory si prostudujte, zejména jejich strukturu a funkci v rámci celku. Příkazy ze skriptů si poté můžete vyzkoušet postupně zadat ručně do terminálu gnuplotu, který spustíte programem wgnuplot.exe (u samotného ovšem nefunguje příkaz help).

Máte-li enormní zájem využívat gnuplot a nepodařilo-li se vám po dlouhém snažení ani samostudiu vyřešit nějaký problém, konzultanti z FYKOSu se vám pokusí poradit – pak jim zašlete všechny soubory, skripty, dávkové soubory, data apod. a dostatečně upřesněte vysněný cíl. K tomuto účelu jsou organizátoři automaticky zcela k dispozici účastníkům na soustředění (v rámci experimentálního odpoledne).

V případě potřeby se také můžete obrátit na nás a konzultovat s námi. V tom případě je nejlepší se obrátit na správce sekce.