Vyhledávání úloh podle oboru

Mějme nekonečnou vodivou uzeměnou desku. Ve vzdálenosti $h$ od ní je umístěn náboj $Q$. Spočtěte, jakou silou je náboj přitahován k desce.

Představte si, že ve vakuu mimo gravitační pole stříkáme vodní paprsek. Kromě tohoto paprsku je zde kolmo (mimoběžně) k jeho původnímu směru umístěn nabitý nekonečný drát s délkovou hustotou náboje $\lambda$. Voda je stříkána z velmi velké vzdálenosti s počáteční rychlostí $v$. Vzdálenost přímky, ve které je stříkána voda (ve které se na začátku pohybuje vodní paprsek) a drátu je $d$. Spočtěte úhel, o který se odchýlí vodní paprsek od původního směru. Molekuly vody si představte jako elektrické dipóly, jejich vzájemné působení zanedbejte a také zanedbejte jejich moment setrvačnosti (tj. představte si, že všechna hmotnost molekuly je soustředěna uprostřed mezi náboji, které jsou nehmotné).

Změřte co nejvíce zdraví neohrožujícími způsoby elektrickou kapacitu člověka.

Mějme nekonečný drát stočený do pravotočivé šroubovice (helixu). Drát je rovnoměrně nabitý a osa helixu je totožná s osou $z$. Do vzniklého pole pošleme nabitou částici (drát je tenký, takže do něj částice nenarazí). V jistém časovém okamžiku známe její $p_{z}$ a $L_{z}$, tedy $z$ové komponenty hybnosti a momentu hybnosti. Můžeme v jiném okamžiku určit $p_{z}$, známe-li v tomto okamžiku $L_{z}?$

(Problém lze vyřešit zcela exaktně. Naproti tomu není určitě nezajímavé zkusit situaci počítačově simulovat a dostat tak hledanou závislost v podstatě experimentálně, v případě ověřit teoretickou předpověď.)

Představme si, že elektrický náboj zeměkoule začne najednou z ničeho nic růst. To znamená, že i vy se začnete nabíjet. Může to dojít tak daleko, že coulombovská síla vyrovná gravitační a vy se odlepíte od Země. Vysvětlete, proč není možné, aby se různě velká tělesa stejné hustoty odlepila ve stejný okamžik. Pro zjednodušení uvažujte, že všechna tělesa mají tvar koule.

Do kapalného dielektrika jsou svisle ponořeny dvě čtvercové paralelní vodivé desky o straně $a$. Nejsou-li desky nabity, vystoupí hladina mezi deskami do výšky $h_{0}$ (měřeno od dolního okraje desek). O jakou vzdálenost $\Delta h$ se zvýší hladina kapaliny mezi deskami, nabijeme-li desky na napětí $U$? Permitivita kapaliny je $\epsilon$, hustota $\rho$ a vzdálenost desek je $d$ ($d << a$).

Tři stejné kuličky o hmotnosti $m$, nabité nábojem $q$, jsou spojeny lehkými neroztažitelnými nitěmi tak, že tvoří rovnostranný trojúhelník o straně délky $d$. Pokud jednu z nití přestřihneme, soustava se začne pohybovat. Určete maximální rychlost „prostřední“ kuličky během nastalého pohybu.

Představte si válcový kondenzátor. Jsou to dva souosé dlouhé válce o poloměrech $r_{1}$, $r_{2}$ ($r_{1}>r_{2})$, na menším je kladná hustota náboje $σ$, na větším stejně velká záporná. Pokud mezi válce vypustíme elektron, může v kondenzátoru obíhat po kruhové dráze. Určete rozsah možných frekvencí, se kterými může elektron v kondenzátoru obíhat. Může obíhat i vně kondenzátoru?

Mějme elektrický dipól (představte si ho jako dvě částice se stejnými hmotnostmi $m$ a náboji $+q$ a $-q$ upevněné na koncích nehmotné tyčky délky $l$). Otáčí se v horizontální (vodorovné) rovině okolo vertikální (svislé) osy procházející středem dipólu. Popište pohyb dipólu poté, co zapneme konstantní vertikální magnetické pole $B$.

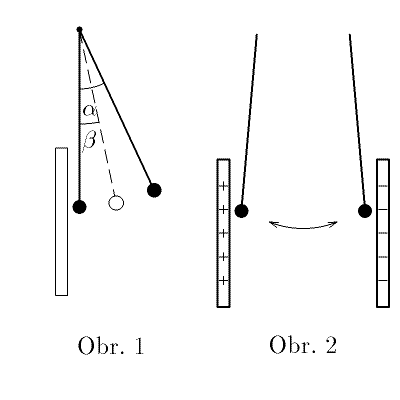
Malá kovová kulička o hmotnosti $m=3,0\,\jd{g}$ je zavěšena na tenkém hedvábném vlákně délky $l=30\;\mathrm{cm}$ tak, aby se dotýkala svislé kovové desky. Kuličku vychýlíme o úhel $α$ a uvolníme. Po odrazu od desky se kulička vychýlí o úhel $β<α$ (obr. 1).

Při druhém pokusu umístíme do vzdálenosti $d=5,0\;\mathrm{cm}$ od první desky druhou stejně velkou. Závěs kuličky prodloužíme, aby byl mnohem delší než vzdálenost desek. Připojíme-li desky ke zdroji vysokého napětí $U=2,00\cdot 10^{4}$ V a závěs vychýlíme, kulička se rozkmitá a naráží střídavě na levou a pravou desku (obr. 2). Perioda nárazů se brzy ustálí na hodnotě $T=0,45\;\mathrm{s}$.

Jak se mění při druhém pokusu rychlost kuličky mezi dvěma nárazy na desky? Jaký náboj nese kulička během letu mezi deskami?