Vyhledávání úloh podle oboru

Uvažte měděný kruhový závit o poloměru $R=10\;\mathrm{cm}$, který leží na stole v magnetickém poli Země (vektor magnetické indukce je rovnoběžný se stolem, který se nachází na rovníku). Poloměr drátu je $r=0,3\;\mathrm{mm}$. Závitem prochází proud $I$. Určete $I$ tak, aby se závit překlopil (předpokládejte, že tření je dostatečně velké, takže závit neproklouzne).

Uvažujme reálnou křemíkovou diodu s přechodovým napětím $0,6 \,\jd{V}$ při pokojové teplotě (fyzici pro jednoduchost považují za pokojovou teplotu $300 \,\jd{K}$, oproti normální $20{^\circ} \,\jd{C} = 293 \,\jd{K}$, protože se s tím lépe počítá a lépe se to pamatuje). Pokuste se z uvedených rovnic (i v minulých dílech seriálu) odhadnout, jak se bude dioda chovat při zvýšení teploty o $10 \,\jd{K}$, $20 \,\jd{K}$ a $40 \,\jd{K}$. Není třeba do puntíku počítat, co se přesně stane, jde pouze o kvalitativní odhady. Ti, kdo mají možnost, mohou odhady ověřit měřením – k měření voltampérové charakteristiky je třeba pouze dioda, ochranný odpor (nikdy nezapojujte diodu v propustném směru přímo na napětí!), zdroj napětí, voltmetr a ampérmetr. Odhady by měly být pro přehlednost aspoň schematicky nakreslené v nějakém grafu. Zaměřte se zejména na velikost závěrného proudu a polohu kolena v propustném směru.

Rezonanční obvod se skládá z neideální cívky s indukčností $L=1\,\jd{ H}$ a vnitřním odporem $R=1\,\jd {Ω}$ a neideálního kondenzátoru s kapacitou $C=1\,\jd{µF}$ o neznámém svodovém odporu $R_{x}$. Jaká je velikost $R_{x}$, pokud víme, že se 1/3 původní energie rezonančního obvodu ztrácí v podobě tepla na odporu cívky?

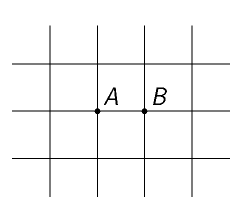
Spočtěte elektrický odpor $R$ mezi body $A$ a $B$ nekonečně rozlehlé čtvercové sítě (viz obr. 1). Jednotlivé úsečky tvořící síť mají odpor $R_{0}$.

Spočítejte kapacitu krychle, jejíž hrany jsou tvořeny kondenzátory o kapacitě $C$. Uvažujte všechna tři možná zapojení krychle do obvodu.

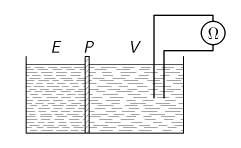
Námětem první experimentální úlohy je jev difúze v kapalině. V kádince je přepážkou $P$ oddělena voda $V$ od roztoku elektrolytu $E$ (např. roztok kuchyňské či jiné soli), viz obrázek. V čase $t_{0}=0 \,\jd{s}$ přepážku odstraníte a ohmmetrem budete sledovat pokles elektrického odporu s časem. Po měření vysvětlete kvalitativně a kvantitativně pozorované změny.

Představte si obyčejnou cívku o $100$ závitech a s konci $A$, $B$. Nyní spojíme konec závitu číslo $57$ s koncem cívky $B$ pomocí dokonalého vodiče. Jak se bude lišit tato cívka od cívky s $57$ závity, budeme-li ji měřit mezi body $A$ a $B$?

Píše se rok 1963. V nejmenovaném pokoji na Strahovských kolejích se připravuje nejmenovaný Student ČVUT na zkoušku z elektřiny a magnetismu. Blíží se vánoce, brzy se stmívá, a tak studenti po celé koleji pomáhají svým unaveným očím svitem žárovek ($60\;\textrm{W}$ za 4,60 Kč, jak se můžete dočíst na obrázcích). Když tu náš Student v zamyšlení pozvedne zrak k jedinému zdroji světla v pokoji, jeho oči sají proud fotonů, myšlenky však bloudí kdesi kolem Maxwellova tenzoru elmag. pole. A jak to tak bývá, ač duchem nepřítomen, podvědomí spustí poplašný signál: „Tady není něco v pořádku.“

Student vyskočí z postele, jsa fotoamatér rychle doběhne pro svůj fotoaparát a nafotografuje dva snímky své svítící žárovky (viz obrázky). Poté jako správný fyzik počne experimentovat. Nejprve si všimne, že žárovka, i když má přerušenou spirálku, svítí pro lidské oko nezměněným jasem. Vypne-li a okamžitě zapne spínač lampy, žárovka svítí vesele dál. Pečlivě si také prohlédne drátky, jež drží wolframovou spirálku v prostoru baňky. Nakonec uzná, že viděl dost, a aby si ověřil, že rozřešil „parafyzikální“ jev v souladu s učebnicí pohozenou na posteli, vypne lampu asi na dvě sekundy a opět zapne. Ocitne se však v nefalšované tmě strahovské noci.

Nakonec poznamenejme, že tento příběh se za hluboké totality skutečně odehrál, fotografie, které jsme se pokusili otisknout v co nejkvalitnější podobě, nejsou podvrhem a vše, co vidíte a co jste se dozvěděli, vás dovede k správné odpovědi na otázku:

„Jak může žárovka s přerušenou spirálkou svítit nezměněným jasem!?“

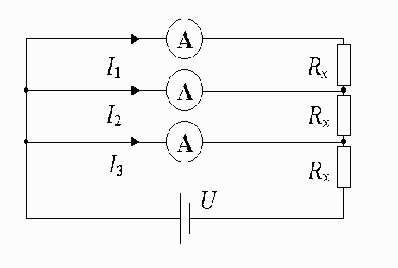
Ampérmetry na obrázku jsou všechny shodné. Odpory $R_{x}$ se také neliší svými hodnotami. Vrchní ampérmetr ukazuje hodnotu proudu $I_{1}=1\;\mathrm{mA}$, střední proud $I_{2}=4\;\mathrm{mA}$. Na spodní ampérmetr nevidíme, neboť je umístěn v ideální tmě. Baterie je plochá, tedy má napětí $U=4{,}5V$. Jaký proud $I_{3}$ teče spodním ampérmetrem a jaká je hodnota odporu $R_{x}?$

Pokuste se změřit odpor spirály elektrického vařiče.

Návod: Ohřívejte vodu vařičem a sledujte závislost její teploty na čase. Z této závislosti zjistěte výkon vařiče, ze kterého už snadno naleznete odpor spirály. Zřejmě vám už došlo, že tato úloha je takzvaně experimentální.