Vyhledávání úloh podle oboru
Databáze úloh FYKOSu odjakživa
astrofyzika (85)biofyzika (18)chemie (24)elektrické pole (71)elektrický proud (76)gravitační pole (81)hydromechanika (146)jaderná fyzika (44)kmitání (57)kvantová fyzika (31)magnetické pole (43)matematika (89)mechanika hmotného bodu (298)mechanika plynů (87)mechanika tuhého tělesa (221)molekulová fyzika (72)geometrická optika (78)vlnová optika (65)ostatní (167)relativistická fyzika (37)statistická fyzika (21)termodynamika (155)vlnění (51)
mechanika plynů
4. Série 10. Ročníku - P. fotbalistický problém
Fotbalista vykopne míč a udělí mu kromě posuvné rychlosti i rotaci okolo svislé osy. Na kterou stranu od původního směru se míč začne odchylovat v závislosti na smyslu rotace a proč? Míč považujte za ideální kouli, odpor vzduchu nezanedbávejte.
4. Série 9. Ročníku - 3. stvoření hvězd
Podle jedné z teorií vznikají hvězdy z oblaku mezihvězdné látky (kosmického prachu) smršťováním pod vlivem gravitačních sil. Určete dobu, za jakou se může zformovat hvězda z obrovského kulového oblaku kosmického prachu o hustotě $ρ=2\cdot 10^{–17}\;\textrm{kg}\cdot \textrm{m}^{–3}$. Můžete předpokládat, že se během smršťování částečky hmoty nepředbíhají a na začátku smršťování měly nulové rychlosti (oblak nijak nerotoval, nebyly v něm víry apod.). Zanedbejte také rozměry vzniknuvší hvězdy vůči počáteční velikosti oblaku.
2. Série 9. Ročníku - P. Lomonosův průvan
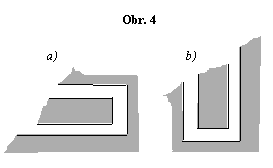
Velký přírodovědec M. V. Lomonosov studoval ve své světově proslulé práci „O volném pohybu vzduchu v dolech“ závislost směru proudění vzduchu na ročním období. Po dlouhém a strastiplném bádání dospěl k závěru, že teplota vzduchu je v dole stále stejná po celý rok. (V jeho době byly doly ještě poměrně mělké.) Určete, jakými směry bude vzduch proudit v létě a v zimě v dolech umístěných podle obr. 4.
1. Série 9. Ročníku - 4. tlak plynu
V nádobě, jejíž stěny mají teplotu $t_{c}$, se nachází plyn o teplotě $t$. V kterém případě bude tlak na stěny nádoby větší: $t>t_{c}$ nebo $t<t_{c}?$
6. Série 8. Ročníku - E. hustota vzduchu
Pokuste se experimentálně určit hustotu vzduchu, pokud máte k dispozici dva různě velké balónky napuštěné plynem lehčím než vzduch. (Nevíme, jak je to s pouťovým šílením v této době jestliže neseženete vhodný plyn, např. vodík, zkuste použít horký vzduch – chyba měření bude ovšem ďábelská. Případně můžete měřit s plynem těžším vzduchu).
Nápověda: Neznámé hustoty náplně balónku se při výpočtu zbavíte právě tím, že provedete měření pro dva různé balónky, čili ze dvou rovnic tuto neznámou vyloučíte.
4. Série 8. Ročníku - 2. jak asi táhne komín
Vertikální roura výšky $h=1\;\mathrm{m}$ s plochou podstavy $S=50\;\mathrm{cm}^{2}$ je z obou stran otevřená. V dolní části roury se nachází ohřívač o výkonu $N=100\; \textrm{W}$. Jaká bude rychlost proudění vzduchu v troubě? Lze předpokládat, že veškerý tepelný výkon ohřívače se spotřebuje na ohřátí vzduchu. Atmosférický tlak je $p_{0}=100\; \textrm{kPa}$, teplota okolního vzduchu $t=20\;\mathrm{°C}$. Molární tepelná kapacita vzduchu při konstantním objemu je $C_{V}=2,5\; \textrm{R}$, kde $R$ je plynová konstanta.
3. Série 8. Ročníku - 3. polytropa na zahřátí
Pod pojmem polytropický rozumíme v termodynamice proces charakterizovaný rovnicí $pV^{α}=\;\mathrm{konst.}$, kde $α$ je daný parametr. Pro vhodné $α$ dostáváme např. izobarický ($α=0$), izotermický ($α=1$) nebo izochorický ($α=∞$) děj. Mějme nejjednodušší případ ideálního jednoatomového plynu. Při jakém polytropickém ději (t.j. pro jakou hodnotu $α$) se v něm zachovává
- počet srážek atomů v jednotce objemu
- celkový počet srážek?
2. Série 8. Ročníku - 1. přistání kosmické sondy
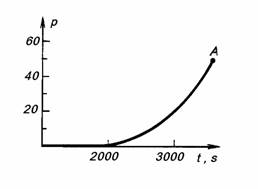
Graf závislosti
Přistávací modul kosmické lodi se přibližuje k povrchu planety s konstantní rychlostí, přičemž předává na kosmickou loď údaje o tlaku atmosféry. Graf závislosti tlaku na čase je na obrázku. Při přistání na povrchu planety modul naměřil teplotu $T=700\; \textrm{K}$ a tíhové zrychlení $g=10\;\mathrm{m}\cdot \mathrm{s}^{-2}$. Určete rychlost $v$, kterou modul přistává, když se atmosféra skládá z oxidu uhličitého. Určete teplotu $T_{h}$ ve výšce $h=12\;\mathrm{km}$ nad povrchem planety.
2. Série 8. Ročníku - 3. nehoda ve vakuu
Dva kosmonauti se nacházejí v otevřeném mezihvězdném prostoru. Neočekávaně dojde k přetržení přívodní hadice u jednoho z nich a následně úniku veškerého vzduchu ze skafandru. Jeho přítel duchaplně připojí ventil ze svého skafandru na utržený konec hadice. Jenže ouha! Hadice je ucpaná a ke zprůchodnění trubice je třeba přetlaku alespoň $1,1\; \textrm{atm}$. Přitom standardní tlak udržovaný přístroji ve skafandru je roven $1\; \textrm{atm}$. Rozhodnou se k následujícímu kroku: vypnou přívod vzduchu nepoškozeného skafandru a společně se vystaví velmi intenzivnímu záření blízké hvězdy, čímž se jejich teplota zvýší z původních $27^{\circ}\;\textrm{C}$ na $107^{\circ}\;\textrm{C}$. Po vyrovnání tlaku rozpojí hadice a rychle se vrátí do stínu solárního článku, kde jejich teplota klesne k normálu. Jakého tlaku dosáhnou touto operací v poškozeném skafandru?
Poznámka: Komu se zdá tato příhoda příliš fantastická nebo málo vědecká, může stejnou úlohu počítat pro dvě identické nádoby spojené hadicí s jednosměrně propustnou klapkou.
1. Série 8. Ročníku - 4. setrvačnost
V autobuse (jede z pouti a má zavřené nejen dveře, ale i okna) stojí cestující a drží na provázku svůj balónek plný helia. Autobus, který původně stál v klidu, se rozjíždí. Co se stane s balónkem? (Cestující je pevně spojen s autobusem –tj. dobře se drží.) Jakým směrem se balónek pohne? Vysvětlete souvislost se setrvačnou silou! Můžete si to také vyzkoušet.