Vyhledávání úloh podle oboru

Při pohybu rychlostí srovnatelnou s rychlostí světla dochází ke kontrakci délek, ale zároveň se nám předmět zdá delší než ve skutečnosti je (zkuste sledovat paprsky světla vyslané z bližšího a vzdálenějšího konce tělesa). Vypočítejte, jestli se u relativistické koule tyto efekty nevyruší.

Bohatý vesmírný turista si zaplatil výlet do hlubokého vesmíru. Raketa vyletí ze Země a rovnoměrně zrychluje se zrychlením $a$, což si turista může ověřit například pouštěním míčku. Nudnou cestu si krátí zíráním ze zadního okénka, pozorováním Země. Po nějaké době (Jaké? Aspoň řádový odhad.) se mu začne zdát, že něco není v pořádku – Země se pomalu přestává zmenšovat. Z toho usoudí, že raketa zpomaluje, což neodpovídá tomu, že raketa stále má zrychlení $a$. To ale turistu nenapadne a rozlobeně jde za kapitánem požadovat vysvětlení. Co mu kapitán řekne?

Předpokládáme, že turista vidí celé elektromagnetické spektrum a má železné nervy a pozorování vydrží.

Pokuste se o řešení libovolného problému z šesté kapitoly seriálu.

Ráma cestuje mezi hvězdami tak, že polovinu času rovnoměrně zrychluje a polovinu času rovnoměrně zpomaluje. Právě se pohybuje kolem Slunce po parabole s vrcholem na orbitě Země. Energii získává ze slunečního záření (žádný reaktor nebo obří baterie jsi na něm neobjevil) a jeho povrch absorbuje 80 % dopadající energie. Nasbírá při průletu sluneční soustavou dostatečnou energii, aby se dostal k Siriu, který je vzdálen 12 světelných let, za 24 let?

Dva stejné náboje umístíme na oba konce tuhé nevodivé tyčky. Jaký výkon budeme potřebovat na otáčení tyčky konstantní úhlovou rychlostí kolem osy procházející středem tyčky. Tření zanedbejte.

Mějme spojku o ohniskové vzdálenosti $f$. Zdroj světla je na ose ve vzdálenosti $a>f$ od čočky, za kterou vzniká jeho obraz. Zdrojem začneme pohybovat určitou rychlostí směrem k čočce. Určete, jak rychle se pohybuje obraz. Rozhodněte, zda tato rychlost může být i nadsvětelná. Bylo by to v rozporu s principy speciální teorie relativity?

Pokud stlačíme hvězdu (či jakékoliv jiné těleso) na kouli o poloměru $r_{g}$, zhroutí se nenávratně do černé díry. Tzv. Schwarzschildův poloměr $r_{g}$ si lze v klasické analogii představit jako poloměr tělesa o hmotnosti $M$, z jehož povrchu lze uniknout pouze rychlostí světla (úniková rychlost je $c$).

Na základě znalosti hmotnosti hvězdy $M$ určete Schwarzschildův poloměr $r_{g}$ a kritickou hustotu hvězdy $ρ$, při které se přemění v černou díru. Příklad řešte obecně a poté konkrétně pro Zemi, Slunce a jádro galaxie o hmotnosti 100 miliard Sluncí.

Změřte rychlost světla ve vakuu. Provést to můžete libovolným způsobem, použijte třeba i mikrovlnnou troubu.

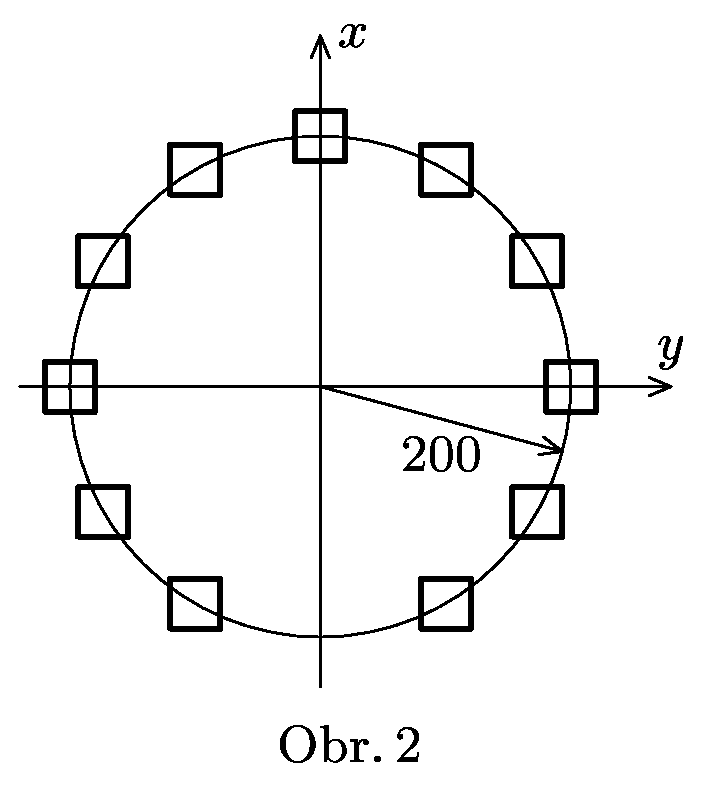
Představte si, že v raketě prolétáváte nad Stonehenge. Ten je tvořen kameny ve tvaru kvádrů rozmístěných do vrcholů pravidelného dvanáctiúhelníku (viz obrázek 2) o poloměru $200$. Letíte nad osou $x$ ve výšce $z=50$ a díváte se vodorovným směrem. Když jste v bodě o souřadnicích ($-200$, $0$), resp. ($0$, $0$), uvidíte svět přesně tak, jak je zobrazen na obrázku 6, přičemž oba máte shodné oči (tzn. např. stejný zorný úhel). Z obrázků přibližně určete poměr rychlosti rakety a rychlosti světla.

Jeden z vítězů Superstar narazil na problém. Jeho nová limuzína je příliš dlouhá na to, aby se vešla do jeho staré garáže. Jeho kamarád, který studuje fyziku, si však věděl rady. Jelikož dobře zná práci Alberta Einsteina, uvědomil si, že pokud se limuzína rozjede dostatečně rychle, zkrátí se její délka z pohledu stojícího pozorovatele natolik, že se již do garáže vejde.

Na začátku a na konci garáže jsou umístěny padací dveře, které se spustí ve chvíli, kdy celá limuzína bude uvnitř. Z pohledu superstar v limuzíně se však naopak v důsledku kontrakce délek zkrátí garáž a vůz se do ní určitě nevejde. Rozhodněte, zda je možné tímto způsobem limuzínu do této garáže zaparkovat.