Vyhledávání úloh podle oboru

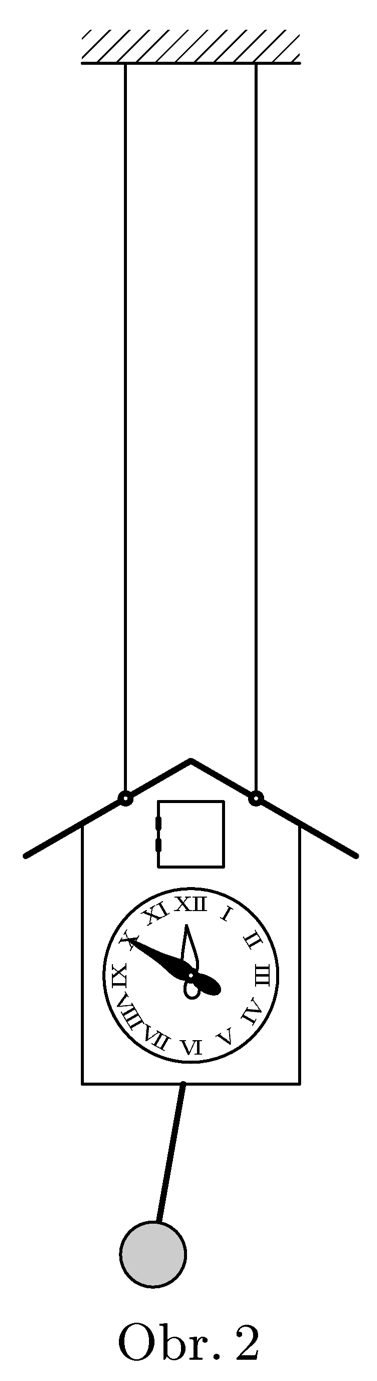
Kyvadlové hodiny o hmotnosti $M$ jsou zavěšeny na dvou dlouhých rovnoběžných lanech (viz obr. 2). Kyvadlo se skládá ze závažíčka o hmotnosti $m$ a lehké tyčky o délce $l$. Určete, o kolik se budou takové hodiny předbíhat (opožďovat) oproti hodinám pevně přibitým na stěně.

Na hřídeli elektromotoru je navinuta nit, na konci které je zavěšeno závaží o hmotnosti $m$. Pokud motor připojíme na ideální zdroj napětí $U$, závaží pojede vzhůru rychlostí $v_{1}$. Jakou rychlostí bude závaží klesat, pokud zdroj odpojíme a vstup elektromotoru zkratujeme? Mechanické tření neuvažujte.

Kdesi v dalekém vesmíru za 1001 hvězdami a jednou černou dírou byla nebyla planeta Balónků. Tyto inteligentní duté bytosti každý rok pořádají soutěž „Čím výš, tím líp“.

Každý z balónků si přiváže provázek, aby bylo možné určit jeho výšku. Aby se mohli Balónci účastnit soutěže, musí mít všichni stejné parametry. Kupodivu nikdo zatím nikdy nevyhrál. Délková hustota provázku je 11 luftíků na špurgl, hustota atmosféry je 110101 luftíků na krychlový špurgl, poloměr každého z balónků je 10 špurglů, hmotnost Balónka je 10 luftíků. Při pádu tělesa v tíhovém poli na planetě Balónků se za každý temp jeho rychlost zvýší o 111 špurglů za temp. Určete, jakou maximální výšku Balónka hlavní rozhodčí soutěže naměří a jak se bude Balónek pohybovat po dosažení této výšky. Nezvednutá část provázku každého Balónka leží volně na zemi. Závody Balónků probíhají v malých výškách, kde je hustota atmosféry přibližně konstantní.

Nápověda: Každý balónek má maximálně jeden provázek.

Ve stojící tramvaji visí u svislé desky na niti délky $l$ propiska o hmotnosti $m$. Tramvaj se rozjede se zrychlením $a$, které můžeme považovat za konstantní. Vypočítejte, kam až toto kyvadlo vykývne (jaký maximální úhel bude nit svírat s deskou) a kdy tužka opět ťukne do desky.

Lokomotiva s osmi vagóny o hmotnosti $40\, \jd{t}$ se rozjíždí na dráze $1\, \jd{km}$ na rychlost $120\, \jd{km \cdot h^{-1}}$ . Jaká musí být minimální hmotnost lokomotivy tohoto vlaku, aby se vlak rozjel bez prokluzování kol na kolejnici?

Počítejte se součinitelem klidového tření $f=0,2$. Odpor vzduchu a valivý odpor zanedbejte.

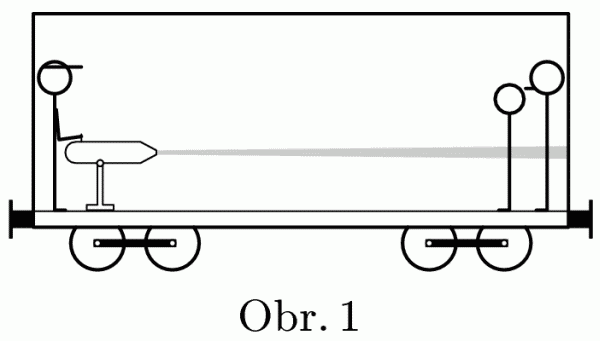
Fanoušci Baníku jeli do Prahy na Spartu. Policisté však byli po špatných zkušenostech připraveni a do vagónu nainstalovali vodní dělo.

Na půli cesty, když vlak zrovna stál v České Třebové, baníkovci začali demolovat vybavení vagónu (jenž váží $30\, \jd{t}$). Policisté nechali dotyčný vagón odpojit a briskně využili své zbraně. Za minutu na fanoušky vystříkali tisícilitrovou nádrž. O jakou vzdálenost proto popojel vagón dlouhý $30\, \jd{m}$?

Předpokládejte, že vagón je odbržděný a že voda z vagónu může vytékat pouze ve svislém směru. Změnu hmotnosti vagónu způsobenou odtokem vody můžete zanedbat.

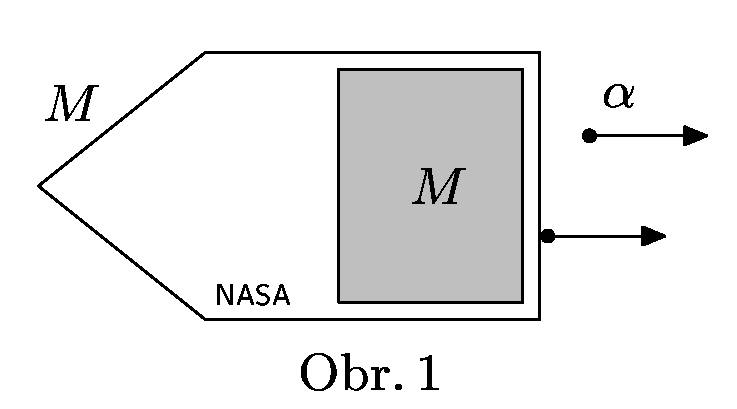
Jet Propulsion Laboratory v Kalifornii vyvíjí pro NASA nový typ raketových pohonů. Pohonná jednotka využívá hybnost $α$-částic při rozpadu nuklidu fermia $^{257}_{100}Fm_{157}$, jehož hmotnost je $m_{Fm}$ a poločas rozpadu $T$. Druhým produktem přeměny je nuklid kalifornia $^{253}_{98}{Cf}_{155}$. Hmotnost $α$-částice je $m_{α}$, hmotnost nuklidu kalifornia je $m_{Cf}$, přeměnou se uvolní energie $E$. Předpokládejte, že každá $α$-částice opouští raketu ve stejném směru.

Vesmírná sonda s popsaným pohonem je na počátku v klidu, její hmotnost je $M$, hmotnost pohonné látky je také $M$. Určete rychlost sondy $v$ po přeměně poloviny hmotnosti nuklidů fermia. Výslednou hodnotu dopočítejte i číselně pro hodnoty $E = 1,106\cdot 10^{-12}\, \jd{J}$, $M = 4\, \jd{kg}$ a $T = 100,5\, \jd{dní}$, ostatní hodnoty najdete v tabulkách.

Langrangián částice v elektromagnetickém poli je $L=\frac{1}{2}mv-qφ+q v\cdot A=\frac{1}{2}m\cdot \sum_{i=1}^{3}v_{i}-qφ+q\cdot \sum_{i=1}^{3}v_{i}A_{i}$,

kde $φ$ je elektrický potenciál a $A$ magnetický vektorový potenciál.

• Určete zobecněné hybnosti částice $p_{i}$ příslušející rychlostem $v_{i}$.
• Napište Hamiltonovu funkci (v proměnných ($x_{i}$, p$_{i})!)$.
• Řešte Hamiltonovy rovnice, je-li $A=0$ a $φ=-Ex_{1}$.

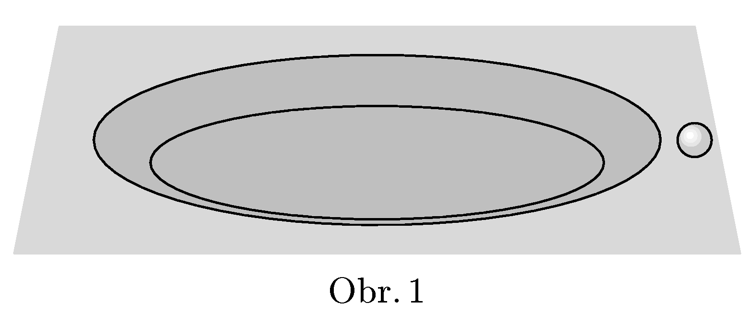
Malý Karlík si hraje s kuličkou. Při cvrnkání je však neopatrný, kulička se mu odkutálí k nakloněné rovině, kterou doma mají místo schodiště, a začne po ní klouzat dolů. Kulička se pohybuje tak, že vektor její rychlosti $v$ svírá s horní hranou nakloněné roviny úhel $φ$. Vypočítejte vektor rychlosti $v′$ kuličky (tj. jeho velikost a také směr) pod nakloněnou rovinou, jejíž výška je $h$. Tření mezi kuličkou a zemí je malé, proto ho zanedbejte. Předpokládejte, že horní a dolní hrana nakloněné roviny je zaoblená, takže se kulička neodlepí od podlahy.

Jako bonus můžete vypočítat, jak se změní směr rychlosti kuličky, která proletí válcovou jamkou o poloměru $R$ a hloubce $h$ se zkosenými hranami (viz obr. 1). Délku zkosení můžete vzhledem k poloměru jamky zanedbat.

V následujících úlohách ověříme vaši znalost všech dosud probraných kapitol mechaniky, tj. Newtonova formalismu, D'Alembertova principu a Lagrangeova formalismu.

1. Představte si planetu Merkur obíhající kolem Slunce. Jak známo, jeho eliptická trajektorie se stáčí (posouvá se poloha perihélia), což nemůže být způsobeno gravitační silou $F=κ(mMr)⁄r^{3}$. Dokažte, že když k této síle přidáme dodatečnou centrální sílu $F=C(r)⁄r^{4}$, kde $C$ je vhodná konstanta, celá trajektorie (elipsa) se bude otáčet konstantní úhlovou rychlostí (čili existuje vztažná soustava otáčející se konstantní úhlovou rychlostí taková, že trajektorie v ní bude elipsa). Znáte-li tuto úhlovou rychlost $Ω$, určete konstantu $C$. Stačí takováto oprava k záchraně Newtonovy teorie gravitace?
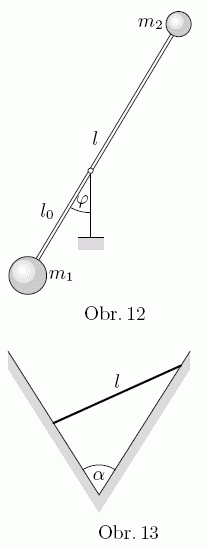
2. Určete rovnovážné polohy homogenní tyčky délky $l$ opřené o vnitřní stěny jamky ve tvaru písmene „V“ (viz obr. 12) v závislosti na vrcholovém úhlu jamky $α$.
3. Pomocí Lagrangeových rovnic vypočítejte periodu malých kmitů dvojzvratného kyvadla na obrázku 13. Závaží na koncích nehmotné tyčky délky $l$ mají hmotnosti $m_{1}$ a $m_{2}$, vzdálenost bodu závěsu od závaží o hmotnosti $m_{1}$ je $l_{0}$.