Vyhledávání úloh podle oboru
Databáze úloh FYKOSu odjakživa
astrofyzika (85)biofyzika (18)chemie (24)elektrické pole (71)elektrický proud (76)gravitační pole (81)hydromechanika (146)jaderná fyzika (44)kmitání (57)kvantová fyzika (31)magnetické pole (43)matematika (89)mechanika hmotného bodu (298)mechanika plynů (87)mechanika tuhého tělesa (221)molekulová fyzika (72)geometrická optika (78)vlnová optika (65)ostatní (167)relativistická fyzika (37)statistická fyzika (21)termodynamika (155)vlnění (51)
mechanika tuhého tělesa
1. Série 21. Ročníku - 4. zachraňte pivo
Nákladní automobil jedoucí rychlostí $v$ veze láhve piva. Řidič si náhle všiml, že po ujetí vzdálenosti $d$ ho čeká nebezpečná zatáčka, která má poloměr $R$. Vžijte se do řidiče a vymyslete, jakou taktiku zvolit při brzdění, jestliže počet rozbitých láhví piva je úměrný největšímu zrychlení a vy jich chcete rozbít co nejméně. Zbytek piv můžete za odměnu vypít.
Vymyslel Marek Pechal při jízdě narvanou 112kou.
6. Série 20. Ročníku - 1. tři válce děda Vševěda
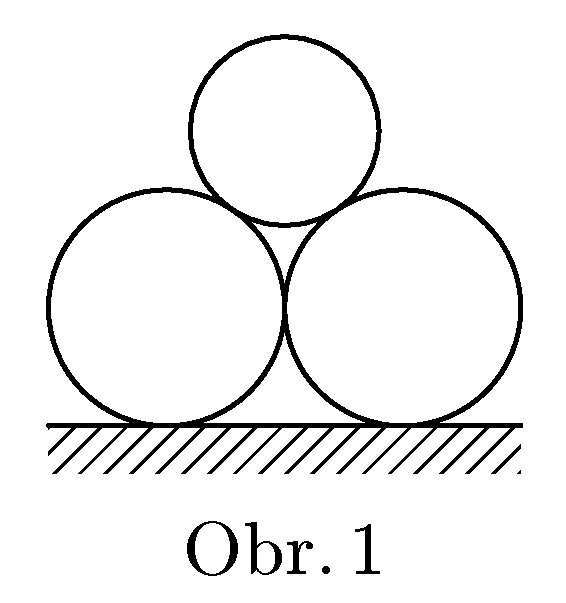
Zjistěte, za jakých podmínek bude soustava tří válců na obrázku 1 v rovnováze. Hustota materiálu válců je $ρ$, spodní válce mají poloměr $R$, horní válec má poloměr $r$. Součinitel tření je mezi všemi povrchy stejný.
Zadal Honza Prachař, aby prověřil vaše znalosti ze statiky soustavy tuhých těles.
5. Série 20. Ročníku - 2. kapitán Kork opět zasahuje
Deník kapitána Korka: „Hvězdný čas 51824,2. Budoucnost hvězdné flotily je znovu ohrožena. Romulani se nás pokoušejí zničit. Zaútočila na nás jejich nová bitevní loď typu Karusel s laserovým otáčivým dělem. Doktor Spok rozhodl, že není možno se s nimi utkat a musíme zaujmout výhodnější postavení co nejdále od nepřítele. Náš palubní vědecký pracovník bohužel ale zrovna spí a my ho nechceme budit. Jsme zřejmě odsouzeni k záhubě …“
Poraďte kapitánovi, jaký manévr má provést, aby unikl jisté zkáze. Hvězdná loď Enterprise má tvar koule o poloměru $R$, na začátku je ve vzdálenosti $r_{0}$. Dělo Karuselu se otáčí úhlovou rychlostí $ω$ a střílí vždy do míst, kde jeho laserový senzor zjistí přítomnost Enterprise. Jakou nejmenší rychlostí se může Enterprise pohybovat, aby Karuselu ještě unikla?
Úloha z hlavy Jardy Trnky. Volné pokračování úlohy III.4 ze 17. ročníku.
5. Série 20. Ročníku - 4. exhumace dárečku od Buffala
Buffalo Bill se už roky snaží polapit Jessieho Jamese, známého banditu. V městečku Clay County mu konečně přišel na stopu. Strhla se přestřelka. Buffalo si všiml sudu plného petroleje na vozíku mezi sebou a Jessiem. „Jak dostat sud k Jessiemu, abych ho mohl zapálit,“ rozmýšlí Bill.
Jessie prostřelil sud v 9/10 výšky a ze sudu začal stříkat petrolej. Buffalo se trefil přesně do poloviny sudu a střílí znovu. Vyřešte, s jakým počátečním zrychlením se bude pohybovat vozíček v závislosti na tom, kam se Bill trefí podruhé. Předpokládejte, že hybnost kulky je nulová, a tření zanedbejte.
Do jaké výšky by se musel Buffalo trefit, aby petrolej stříkal nejdále?
Znovu zadaná úloha V.1 z 18. ročníku, protože tehdejší řešení je špatně. Přílepek od Honzy Hradila.
4. Série 20. Ročníku - 1. nakupujeme minerálky
Určitě jste si v super(hyper)marketu všimli, že plastová láhev oblíbeného nápoje se při rozjetí pohyblivého pásu pokladny začne otáčet a k pokladní ji často musíte postrčit až rukou. Proč to tak je?
Zkuste analyzovat následující modelový případ. Láhev je položena na pás osou kolmo na směr pohybu pásu a láhev i pás jsou v klidu. Náhle se pás rozjede konstantní rychlostí $v=10\, \jd{cm\cdot s^{-1}}$. Jakou výslednou rychlostí se bude pohybovat láhev? Nejdříve analyzujte, jak se budou chovat různé idealizace – jako třeba tuhý válec. Pak si uvědomte, že láhev je plná nápoje, který se nerad otáčí. Pro jednoduchost uvažujte viskozitu nápoje za nulovou, pak se zamyslete nad tím, jak do hry vstoupí viskozita.
Úlohu vymyslel Jano Lalinský na nákupu v TESCU.
4. Série 20. Ročníku - 4. Kochova vločka
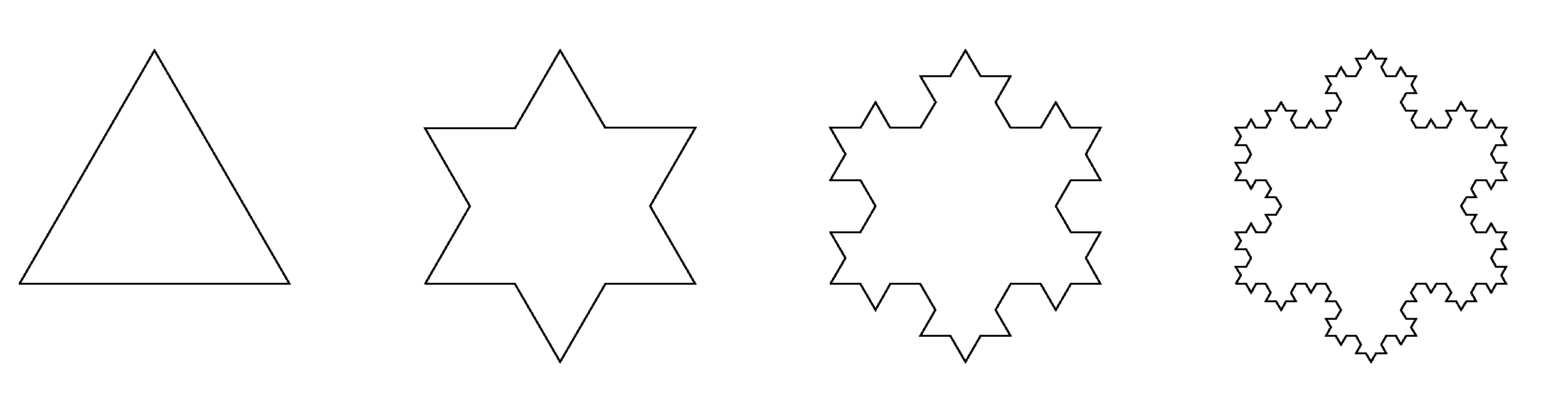
Určete moment setrvačnosti Kochovy vločky zhotovené z homogenního plechu vzhledem k ose kolmé na její rovinu a procházející jejím středem. Uvažujte, že vločka má hmotnost $m$ a průměr $a$.
Poznámka: Kochova vločka je útvar vzniklý iterativním lepením vždy třikrát menších rovnostranných trojúhelníků na strany předchozího útvaru (viz obrázek). Průměrem Kochovy vločky rozumíme vzdálenost vrcholů jejích protějších cípů.
Problém si s chutí vyřešil Marek Pechal.
4. Série 20. Ročníku - E. vytřete nám zrak
Změřte, jak závisí součinitel smykového tření mezi dvěma vámi vybranými materiály na velikosti stykové plochy a na hmotnosti smýkajícího se tělesa. Nezapomeňte nám napsat, s čím a jak jste měřili.
Úloha napadla Honzu Prachaře při čtení Feynmanoých přednášek z fyziky.
3. Série 20. Ročníku - 2. přistání na Titanu
V pátek 14. ledna 2005 na povrchu Titanu hladce přistála sonda Huygens, pojmenovaná po objeviteli Titanu. Mateřská sonda Cassini ji nesla k Saturnu 7 let. Jedná se dosud o nejvzdálenější přistání umělé sondy v dějinách.
Přistávací modul o čisté hmotnosti (bez paliva) $m$, vybavený reaktivním motorem, se vznášel v klidu nad povrchem měsíce (gravitační zrychlení je zde $g)$. Měl k dispozici palivo o hmotnosti $M$ a zásobu energie o velikosti $E_{0}$, kterou využíval k urychlování paliva (rychlost a množství paliva vypuzovaného z motoru lze libovolně měnit). Jaká je maximální doba, po kterou se sonda mohla vznášet v konstantní výšce? Poraďte řídícímu středisku, jakým způsobem by mělo naprogramovat rychlost a množství vypuzovaného paliva, aby této maximální doby dosáhli.
Úlohu vymyslel Marek Pechal.
3. Série 20. Ročníku - P. akrobat na lyžích
Jistě znáte lyžařskou disciplínu akrobatické skoky. Lyžař po rozjezdu z kopce najíždí na můstek a skáče do vzduchu. Před dopadem zvládne skokan provést několik vrutů a salt. Vysvětlete, jak to lyžař dělá – co musí udělat, aby se začal otáčet tak, jak chce. Jak vyvrátíte tvrzení, že podle zákona zachování momentu hybnosti se musí skokan po celou dobu skoku otáčet kolem stejné osy a stejnou rychlostí?
Problém vrtal hlavou Honzy Prachaře při sledování zimní olympiády.
1. Série 20. Ročníku - 2. srážka s asteroidem
Určete, jaký úhel po srážce svírala trajektorie asteroidu a vědecké lodi. Před srážkou byl kulový asteroid v klidu a měl stejnou hmotnost jako loď. Uvažte, že loď chrání štíty, které mají kulový tvar.
Úlohu navrhla Zuzka Safernová.