Vyhledávání úloh podle oboru

Žebřík vede jen dva kilometry na plošinu, ze které se dále sestupuje po schodech, jež se mohutným obloukem klenou nad krajinou. Schodiště má zvláštní tvar. Je totiž postavené tak, že se na každý krok vynaloží stejná práce. Odvoď, jak závisí výška schodu na vzdálenosti od osy Rámy, pokud je délka schodů konstantní. Také můžeš určit, jaký tvar má onen oblouk.

Úspěšně ses dostal na povrch Rámy. Z ničeho nic se Ráma několikrát otřásl a zdá se ti, že se změnila rychlost jeho rotace. Tato otázka tě velice tíží. Navrhni proto několik způsobů, jak bys změněnou periodu rotace určil.

Předmětem této úlohy je, abyste odhadli, jak by se změnila rychlost rotace Země, kdyby Angličani a Skoti začali jezdit vpravo místo vlevo.

Určete, jaké fyzikální vlastnosti musí mít materiál závěsného lana výtahu, který spojuje povrch Země a oběžnou geostacionární dráhu. Je vůbec takový materiál na Zemi dostupný?

Malou kuličku hodíme vodorovně na nakloněnou rovinu. Kulička po ní začne poskakovat a po $N$ odrazech dopadne kolmo k povrchu nakloněné roviny (příklad trajektorie kuličky pro $N=4$ viz obrázek). Jaký je úhel $α$ nakloněné roviny? Předpokládejte, že se kulička odráží dokonale pružně, rotaci kuličky neuvažujte.

Představte si, že jedete rychlíkem. Díváte se ven z otevřeného okna a sledujete okolní krajinu. O tři okna dál po směru jízdy nějaký zákeřný lump vyplivne žvýkačku. Kolik času máte, aby jste stihli uhnout? Samozřejmě přepokládáme, že žvýkačka je dokonalá koule a z okna nebyla vyhozena, nýbrž vlastně položena do proudu vzduchu.

Navrhněte sklon a tvar předního skla automobilu tak, aby z něj kapky dešťové vody při rychlosti auta $80\,\jd{ km ⁄ h}$ nestékaly dolů, ale do stran. Ověřte, zda váš výsledek odpovídá skutečnosti. Co dalšího určuje sklon čelního skla?

Prozkoumejte skutečnost, že se při pohledu z jedoucího vlaku vzdálenější objekty na horizontu zdánlivě pohybují po okně pomaleji, zatímco sloupy u trati se jen tak mihnou. Jak závisí tato zdánlivá rychlost pohybu krajiny na její vzdálenosti od cestující veřejnosti?

Chováte neposlušného kozla, jehož oblibou je přeskakovat plot k sousedům. Nahánění kozla už máte pokrk, proto jste nakoupili vyšší pletivo, kterým chcete svůj pozemek nově oplotit. Místo, kde má plot stát, je ve svahu, a tak je situace trochu komplikovanější. Vy si ale jistě poradíte. Pod jakým úhlem plot vzhledem ke svahu postavit tak, aby bylo pro kozla co možná neobtížnější jej přeskočit?

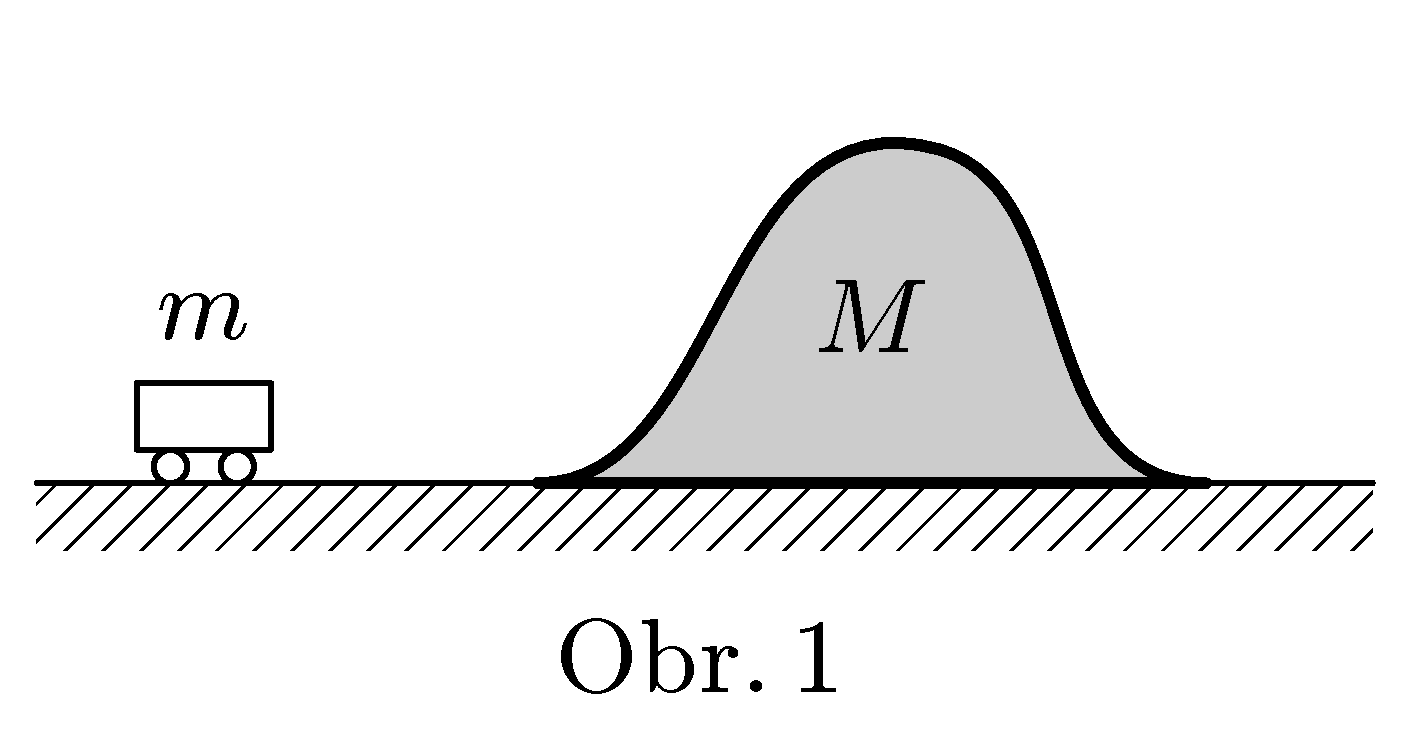
Vozíček o hmotnosti $m$ jede po rovině rychlostí $v$, na níž leží dřevěný „kopeček“ o hmotnosti $M$ a výšce $h$, jenž po rovině klouže bez tření (viz obr. 1). Vozíček na kopeček najede. Za jakých podmínek se mu podaří přejet přes vrchol? Jakou rychlostí se bude hora nakonec pohybovat?