Vyhledávání úloh podle oboru

Dva světaznalí cestovatelé, jeden tlustý a jeden hubený, se cestou v letadle dohadují o tom, kdo z nich by déle přežil v extrémních podmínkách daleko od civilizace. Rozsoudíte je, kdo vydrží déle ve velkém horku (50 °C), v mrazu (-1 °C), po ztroskotání lodi uprostřed Středozemního moře, v hurikánu nebo při silném sněžení? A jak by to mohlo dopadnout, kdyby je zastihlo mohutné zemětřesení v centru velkoměsta? Kromě jejich tělesné stavby mezi nimi nejsou žádné rozdíly, oba jsou stejně oblečení a nic dalšího s sebou nemají (žádné jídlo, vodu, sirky ani jiné vybavení). Snažte se být nápadití a všímejte si i maličkostí.

Na nakloněné rovině s úhlem sklonu $α$ stojí směrem po spádnici vozová hradba. Vozy jsou stejně těžké, mezi sousedními dvěma je vzdálenost $s$, celkem jich je $N$. Na počátku jsou všechny zabržděné. Mazaný bratr Žižka odbrzdí horní z nich a ten se začne pohybovat směrem dolů a bere s sebou další vozy (hned po nárazu se nabouraný vůz odbrzdí a pokračuje dolů spolu s tím, který do něj narazil). Vypočítejte, jakou rychlost bude mít celá vozová hradba po posledním nárazu. Jako bonus můžete určit, jaké by měly být hmotnosti vozů tak, aby se rychlost hradby mezi dvěma nárazy nezměnila.

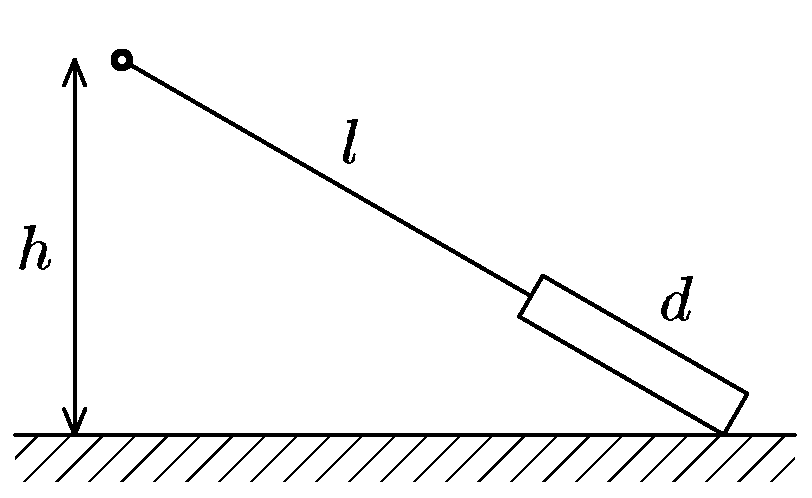
Na pevném závěsu ve výšce $h=1\, \mathrm{m}$ nad zemí je upevněn provázek délky $l=1,5 \;\mathrm{m}$. Na konci provázku je přivázána deska délky $d= 0,5 \;\mathrm{m}$ tak, že provázek je napnut a spolu s deskou leží v jedné přímce (viz obrázek). Když soustavu uvolníme, deska nejprve po hraně klouže bez tření, dokud nedopadne celou svou délkou na zem. Potom se pohybuje proti třecí síle s koeficientem smykového tření $f$. Spočítejte, jaká musí být jeho hodnota, aby deska svým bližším koncem doklouzala přesně pod závěs.

Všichni dobře víme, že se 21. prosince 2012 na své cestě ke Slunci srazí se Zemí asteroid (pohybuje se ve stejné rovině jako Země). Uvažme, že se pohybuje po protáhlé eliptické dráze s hlavní poloosou délky 4 AU a vedlejší poloosou dlouhou 0,2 AU. Lidstvo bylo moc zaneprázdněno, a tak se problém začal řešit až 1. prosince 2012. Po jaké dráze musí udatná světová autorita vystřelit raketu s jadernou hlavicí, aby včas odvrátila konec světa?

Kryštof se vydal na cestu vlakem a spokojeně usnul. Když se probudil v tunelu, cítil, že jej nějaká síla táhne směrem na jednu stranu. Ve vlaku bylo sice světlo, ale ven neviděl. Vzpomněl si, že je v zatáčkách trať klopená a uvědomil si, že i když si pamatuje původní směr jízdy, vůbec neví, na kterou stranu vlak zatáčí. Nepozná totiž rozdíl mezi stavem, kdy vlevo zatáčející vlak jede dostatečně pomalu a výsledná síla míří směrem do zatáčky, a situací, kdy je vlak dostatečně rychlý, zatáčí vpravo a síla směřuje ven ze zatáčky. Navrhněte experiment, který Kryštofovi pomůže tuto situaci vyřešit. Čím víc variant, tím lepší bodové hodnocení.

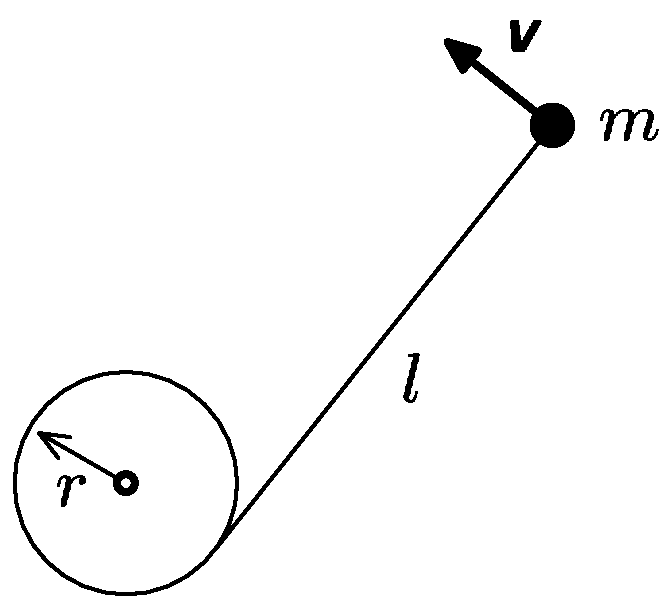
Na kůl o poloměru $r$ zabodený do země je lanem délky $l$ přivázané závaží hmotnosti $m$. Lano je napnuté a závaží leží na zemi. Lukáš se rozběhne a nakopne závaží kolmo na lano tak, že bude mít rychlost $v$. Lano se po tomto rázu začne navíjet na kůl. Spočítejte, jak se musí měnit koeficient smykového tření mezi závažím a zemí v závislosti na vzdálenosti od kůlu, aby při navíjení zůstala rychlost závaží konstantní.

Terka skáče z metrové zídky. Na začátku má ruce natažené zvednuté nad hlavu, během pádu ruce ale spouští. O kolik takto zmenší svou rychlost při dopadu? Kvalifikovaně odhadněte hmotnost, zrychlení a rychlost Terčiných rukou, jakožto i další potřebné parametry jejího těla, a úlohu vyřešte.

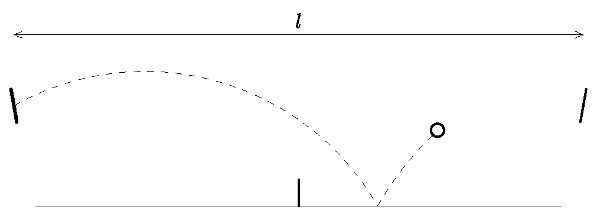
Pana Broučka při měsíční příhodě pronásledovala Etherea, kterou lze připodobnit hmotnému bodu. Pan Brouček ale, potom co si objednal vepřové se zelím, se jí zbavil tím, že ji uvěznil mezi dvěma pevně uchopenými pálkami ve vzdálenosti $l$, které jsou každá natočena o nějaký úhel, a Etherea mezi nimi skákala jako pingpongový míč tak, že se odrazila vždy ve stejné výšce. Aby ji potrápil strachem, vložil doprostřed síť výšky $h$. Pan Brouček je důmyslný šibal, a tak chtěl, aby (stejně jako v ping-pongu) na každé polovině spadla aspoň jednou na zem. Vypočtěte, s jakou frekvencí v závislosti na všemožných parametrech (natočení pálek, počáteční rychlost míčku, úhel, …) Etherea létá, a kdy je tato frekvence nejvyšší. Předpokládejte, že pohyb je rovinný a při odrazu od překážky (od Měsíce nebo od pálky) se akorát mění rychlost na opačnou; celý pohyb probíhá ve vakuu.

Postavte dlouhé domino a hurá do toho! Změřte rychlost padání pro známé rozměry kvádříků a proměnnou vzdálenost mezi nimi. Ustálí se vůbec rychlost?

Zkoumejte dvojitý uzel, kterým jsou spojena dvě vlákna o poloměru $r$ a součiniteli klidového tření $f$. Jakou silou musíme tahat za konce vláken, aby se uzel „proklouzl“? Dosaďte typické hodnoty pro nitky a zjistěte, zda se přitom nepřetrhne vlákno.