Vyhledávání úloh podle oboru
Databáze úloh FYKOSu odjakživa
astrofyzika (85)biofyzika (18)chemie (24)elektrické pole (71)elektrický proud (76)gravitační pole (81)hydromechanika (146)jaderná fyzika (44)kmitání (57)kvantová fyzika (31)magnetické pole (43)matematika (89)mechanika hmotného bodu (298)mechanika plynů (87)mechanika tuhého tělesa (221)molekulová fyzika (72)geometrická optika (78)vlnová optika (65)ostatní (167)relativistická fyzika (37)statistická fyzika (21)termodynamika (155)vlnění (51)
mechanika hmotného bodu
(2 body)6. Série 25. Ročníku - 1. tref svojí družici
Máme malý míček o poloměru $r$ těsně nad míčem o poloměru $R$. Nejspodnější bod spodního míče je ve výšce $h$ nad zemí. Oba míčky pustíme. Do jaké nejvyšší výšky může vystoupit horní míček? Uvažujte, že všechny srážky jsou dokonale pružné. Bez újmy na bodech můžete považovat hmotnost horního míčku za zanedbatelnou.
Bonus: Postup zobecněte na $N$ míčků. (Stále můžete uvažovat, že hmotnost míčku výše je zanedbatelná oproti míčku pod ním.)
Potrefený Karel.
(2 body)6. Série 25. Ročníku - 2. kosmická stanice
Odhadněte, jakou minimální energii musíme dodat kosmické stanici, abychom ji dostali na oběžnou dráhu. Můžete pracovat s hodnotami pro mezinárodní kosmickou stanici ISS, která obíhá Zemi ve výšce cca $h=350\;\mathrm{km}$ a má celkovou hmotnost přibližně $m=450\;\mathrm{tun}$. Vysvětlete, proč je odhad minimální a vyjmenujte alespoň některé fyzikální skutečnosti, které vedou k tomu, že je skutečná spotřeba raket významně vyšší.
Astrokarel.
(4 body)6. Série 25. Ročníku - 3. čerpadlo
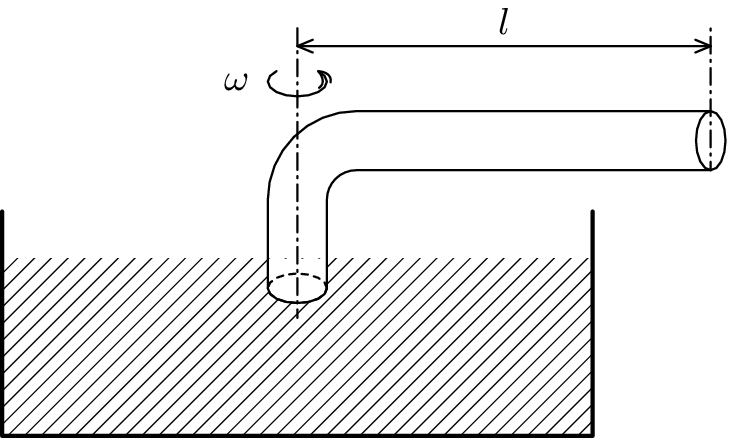
Mějme zahnutou trubici délky $l$ plnou vody, jejíž spodní konec je ponořen do nádoby. Trubicí otočíme jednou za čas $T$. Pod jakým tlakem je nasávána voda z nádobky? Viskozitu vody a tlak sloupce vody ve svislé části zanedbejte.
Vyčerpaný Petr.
(4 body)6. Série 25. Ročníku - 5. běh na přednášku z eugeniky
Aleš sedí pod kopcem u stanu a surfuje na internetu na svém tabletu, když tu si náhle všimne, kolik je hodin a uvědomí si, že vlastně chtěl jít na přednášku. Už je tak pozdě, že bude muset celou cestu běžet a nebude moct zastavit, ani aby se vydýchal. Proto se samozřejmě okamžitě rozběhne svou maximální běžeckou rychlostí $v$ do kopce, který má rovnoměrné stoupání $α$. Po chvíli (čas $T)$ si ale uvědomí, že má v kapse cihlu a že tu cihlu chtěl nechat u stanu. Aleš od sebe umí cihlu hodit jedině rychlostí $w$. Pod jakým úhlem má cihlu v tom okamžiku vyhodit, aby dopadla na kamaráda, co si právě sedl na jeho místo? Může se stát, že nedohodí? Aleš je hodně rychlý, a proto neuvažujte jeho reakční dobu a ani dobu, kterou vám zabere řešení úlohy.
Karel civěl na internet.
(2 body)5. Série 25. Ročníku - 1. šumivý prášek
Hodíme-li do sklenice s vodou šumivý prášek, tak nejprve leží na dně a potom se zvedne. Proč?
Aby předešel chřipce, vymyslel Lukáš.
(2 body)5. Série 25. Ročníku - 2. elektrická rovnováha
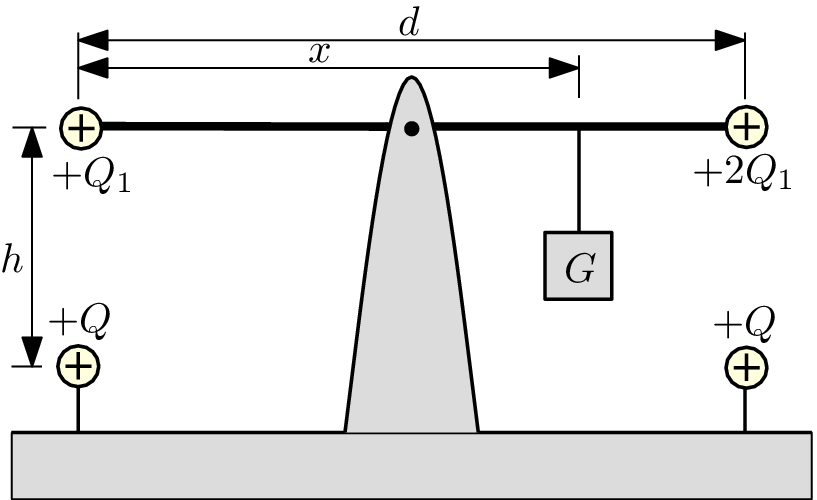
Na obrázku je nevodivá tyč délky $d$ zanedbatelné hmotnosti, otočná kolem svého středu. Na obou koncích tyče jsou připevněny malé vodivé koule zanedbatelných hmotností s kladnými náboji $Q_{1}$ a 2$Q_{1}$. Tyč je vyvážena závažím o tíze $G$ podle obrázku. Ve vzdálenosti $h$ přímo pod každou z koulí je pevně umístěna koule s kladným nábojem $Q$.
- Určete vzdálenost $x$, pro niž je tyč vodorovná a je v rovnováze.
- Pro jakou hodnotu $h$ bude tyč v rovnováze a nebude přitom vůbec zatěžovat čep, na němž je upevněna?
Ze sbírek vyhoupala Dominika.
(5 bodů)5. Série 25. Ročníku - 4. maminka a kočárek
Maminka má kočárek o hmotnosti $m$ a je s ním pevně spojena vláknem délky $l$, které je na počátku natažené. Mezi maminkou i kočárkem a podlahou, na které oba stojí, je nenulový koeficient smykového tření $f$. Maminka začne kočárek táhnout po přímce konstantní rychlostí $v$, která je kolmá na počáteční polohu vlákna. Popište trajektorii kočárku v závislosti na parametrech úlohy. Maminku i kočárek považujte za hmotné body. Doporučujeme úlohu numericky simulovat.
Maturantská.
(4 body)5. Série 25. Ročníku - 5. lovec v2
O kolik musíme zvýšit výkon motoru na jednoho chyceného ptáka za sekundu, pokud nad vagonem vztyčíme síť, do níž chytáme nebohé ptáky? Vlak jede rychlostí $v$, pták váží $m$, jeho rychlost je $w$, úhel nalétnutí do sítě je $φ$ a síť má plochu $S$. Předpokládejte, že mezi jednotlivými záchyty se síť vrátí vždy do klidové polohy.
Orgové jeli vlakem.
(2 body)4. Série 25. Ročníku - 1. schody z Chrudimi
Eskalátory v metru na náměstí Míru mají $n$ schodů a pohybují se rychlostí $v$. Spočtěte, kolik schodů ve skutečnosti vyšlapete, pokud po nich jdete rychlostí $v_{1}$:
a) po směru jízdy,
b) proti směru jízdy.
Při pohybu proti směru uvažujte, že $v_{1}>v$.
Aleš po cestě do otevřených dveří.
(2 body)4. Série 25. Ročníku - 2. gatling
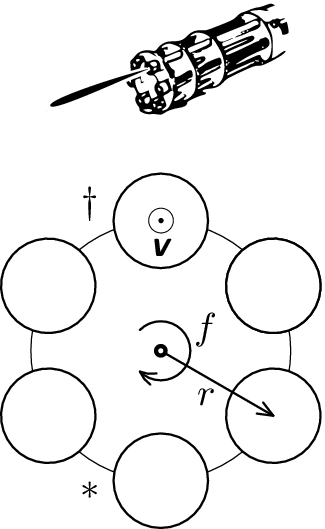
Stroj byl původně navržen pro distribuci semen do země, ale ukázal se jako mnohem užitečnější pro distribuci olova do nepřátel (rotační kulomet). Spočítejte, kde vzhledem k hlavni Gatlingu hrozí nebezpečí zasažení kulkou. Ráže je $d$, počet hlavní $n$, vzdálenost osy hlavně od osy hřídele je $r$, otáčky všech hlavní jsou $f$, kadence výstřelů je $F$ a úsťová rychlost střel $v$.
Napadlo Michala při čtení tajného časopisu.