Vyhledávání úloh podle oboru
Databáze úloh FYKOSu odjakživa
astrofyzika (85)biofyzika (18)chemie (24)elektrické pole (71)elektrický proud (76)gravitační pole (81)hydromechanika (146)jaderná fyzika (44)kmitání (57)kvantová fyzika (31)magnetické pole (43)matematika (89)mechanika hmotného bodu (298)mechanika plynů (87)mechanika tuhého tělesa (221)molekulová fyzika (72)geometrická optika (78)vlnová optika (65)ostatní (167)relativistická fyzika (37)statistická fyzika (21)termodynamika (155)vlnění (51)
mechanika hmotného bodu
(3 body)1. Série 32. Ročníku - 2. ohňostroj
Jáchym odpaloval ohňostroj, který si můžeme představit jako světlici, která je v určitý čas vystřelena rychlostí $v$ směrem svisle nahoru, a poté za nějaký čas vybuchne. Jáchym stál ve vzdálenosti $x$ od místa odpalu, když uslyšel zvuk výstřelu. Za čas $t_1$ uviděl výbuch a za čas $t_2$ po zpozorování výbuchu ho i uslyšel. Spočítejte rychlost $v$.
Jáchym v sobě pyrotechnika nezapře.
(7 bodů)1. Série 32. Ročníku - 4. pád z okna
Když James Bond pustil agenta 006 Aleca Treveljana z konstrukce radioteleskopu Arecibo ve finální scéně filmu Golden Eye, ten začal křičet s frekvencí $f$. Spočítejte závislost frekvence, kterou slyší 007, na čase. Odpor vzduchu neuvažujte.
Nápověda: Pro radu jděte k panu Dopplerovi.
Matěj se rád dívá z ok(n)a.
(10 bodů)1. Série 32. Ročníku - S. teoretická mechanika
Předtím než se začneme věnovat umění analytické mechaniky, je vhodné si zopakovat klasickou mechaniku na následující sérii příkladů.
- Na vrcholu křišťálové koule dřepí homogenní kulička s velmi malým poloměrem. Kuličce udělíme libovolně malou rychlost a ta tak začne padat po povrchu koule. Kde se kulička odpojí od křišťálové koule? Uvažujte, že kulička neprokluzuje.
- Místo koule z předchozí úlohy máme křišťálový paraboloid, daný rovnicí $y = c - ax^2$. Opět nás zajímá, kde se kulička od paraboloidu odpojí?
- Cyklista odbočuje rychlostí $v$ na cestu kolmou k té, po které právě jede. Zatáčku projede po části kružnice s poloměrem $r$. Jak moc se musí cyklista do zatáčky naklonit? Moment setrvačnosti kol bicyklu můžete zanedbat, cyklistu nahraďte hmotným bodem.
Bonus: Moment hybnosti kol nemůžete zanedbat.
(8 bodů)6. Série 31. Ročníku - 5. skok z letadla
Filip o hmotnosti $80 \mathrm{kg}$ vyskočil z letadla, které je ve výšce $h_1 =500 \mathrm{m}$ nad zemí. Ve stejném okamžiku z druhého letadla skočila Danka o hmotnosti $50 \mathrm{kg}$, ale z výšky $h_2 =569 \mathrm{m}$ nad zemí. Předpokládejme, že oba mají stejný odporový koeficient $C = 1{,}2$, Filipova plocha příčného průřezu je $S_f = 2{,}2 \mathrm{m^2}$ a Dančina je $S_d=1{,}5 \mathrm{m^2}$. Hustota vzduchu $\rho =1{,}205 \mathrm{kg\cdot m^{-3}}$ se nemění s výškou. Za jakou dobu od výskoku bude Danka ve stejné výšce nad zemí jako Filip?
Danka uvažovala nad náročným životem Matfyzáka, tak se chtěla trochu odreagovat.
(3 body)5. Série 31. Ročníku - 1. schodisko na Mesiaci
Pokud bychom jednou kolonizovali Měsíc, bylo by vhodné na něm používat schody? Představte si na Měsíci klesající schodiště s výškou schodu $h=15 \mathrm{cm}$ a délkou $d=25 \mathrm{cm}$. Odhadněte počet schodů $N$, které by přeletěl člověk, jestliže před vstupem na schody šel rychlostí $v=5{,}4 \mathrm{km\cdot h^{-1}}=1{,}5 \mathrm{m\cdot s^{-1}}$. Tíhové zrychlení na povrchu Měsíce je šestkrát slabší než na povrchu Země.
Dodo čítal Mesiac je drsná milenka.
(5 bodů)5. Série 31. Ročníku - 3. klín
Klíny
Máme dva klíny o hmotnostech $m_1$, $m_2$ a úhel $\alpha $ (viz obrázek). Vypočítejte zrychlení levého klínu. Předpokládejte, že nikde nedochází ke tření.
Bonus: Uvažujte tření s koeficientem $f$.
Jáchym vykradl skripta ČVUT.
(8 bodů)5. Série 31. Ročníku - 5. záludná kapka
Mějme kulatou kapku o poloměru $r_0$ tvořenou vodou o hustotě $\rho \_v$, která shodou okolností padá v mlze v homogenním tíhovém poli $g$. Uvažujme vhodnou mlhu se speciálními předpoklady. Tvoří ji vzduch o hustotě $\rho \_{vzd}$ a vodní kapičky s průměrnou hustotou $\rho \_r$, když uvážíme, že se rozptýlí zcela rovnoměrně. Jestliže kapka propadne nějakým objemem takové mlhy, vysbírá všechnu vodu, která se v tomto objemu nachází. Na místě zůstane pouze vzduch. Jaká je závislost hmotnosti kapky na vzdálenosti uražené v takovéto mlze?
Bonus: Řešte pohybové rovnice.
Karel chtěl zadat něco, kde se bude měnit hmotnost.
(6 bodů)4. Série 31. Ročníku - 3. divně tvarovaná nádobka
Máme válcovou skleničku, která má zboku u dna malou díru o ploše $S$. Tato nádoba je naplněná vodou, která samovolně přetéká do druhé nádoby, která je tentokrát již bez díry. Jaký tvar by musela mít druhá nádoba, aby v ní hladina rostla rovnoměrně? Předpokládejte, že má být válcově symetrická.
Bonus: Dna obou nádob jsou ve stejné výšce a nádoby jsou dírou spojené.
Karel se díval, jak se nalévá sklenička na rautu.
(7 bodů)4. Série 31. Ročníku - 5. nemožnost nakažení
Představme si, že roztlačíme nějakou bakterii obvyklé velikosti na rychlost $v = 50 \mathrm{km\cdot h^{-1}}$ ve vodorovném směru a necháme ji volně letět ve vzduchu. Jakou vzdálenost zhruba urazí, než se zastaví?
Výsledek vás možná překvapí. Jak je tedy možné se infikovat tímto způsobem bakteriální infekcí? Diskutujte, proč je to možné i přes takový výsledek.
Karel se díval na Youtube na TED-Ed.
(3 body)3. Série 31. Ročníku - 2. zrychleníčko, zrychlení
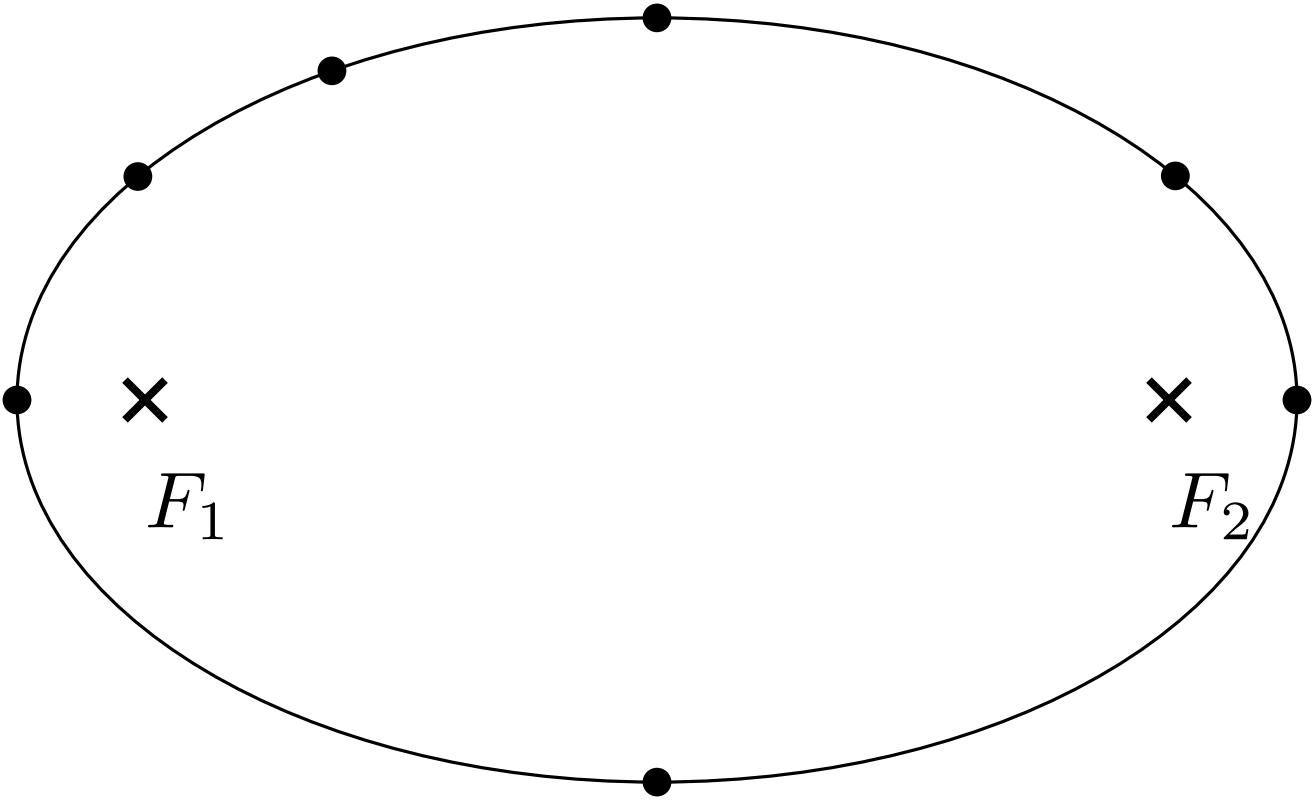
Náčrt elipsy
Na obrázku vidíte náčrt elipsy s ohnisky $F_1$ a $F_2$ a několika vyznačenými body na ní. Uvažujte, že elipsa znázorňuje trajektorii nějakého hmotného bodu. Znázorněte do obrázku zrychlení, která působí na hmotný bod v jednotlivých vyznačených bodech dráhy pro dvě situace (jde o směry a vzájemné poměry zrychlení (které je větší/menší) v různých bodech v rámci jednoho náčrtu).
- V ohnisku $F_1$ je umístěno hmotné těleso, kolem kterého hmotný bod obíhá. Uvažujeme, že platí 2. Keplerův zákon.
- Těleso má konstantní velikost rychlosti, pouze se pohybuje po elipse.
Karel na konferenci slyšel, že s takovými úlohami mají problémy i vysokoškoláci.