Vyhledávání úloh podle oboru

Mějme sériový $RC-obvod$, který připojíme na zdroj periodického napětí s tzv. obdélníkovým průběhem, tzn. po čas $T/2$ je napětí $U$ a po čas $T/2$ napětí $-U$. Jak bude vypadat průběh napětí na kondenzátoru?

Mějme dva přímé rovnoběžné nekonečně dlouhé kovové vodiče zanedbatelného kruhového průřezu, které jsou od sebe ve vzdálenosti $r$. Směr jednotkového vektoru $\textbf{e}_{3}$ zvolme tak, aby byl rovnoběžný s vodiči. Jednotkový vektor, který leží v rovině určené vodiči, je kolmý na $\textbf{e}_{3}$ a má směr z prvního vodiče k druhému, označme $\textbf{e}_{1}$. Jako vektor $\textbf{e}_{2}$ označujme vektorový součin $\textbf{e}_{3}$ × $\textbf{e}_{1}$. Vektory $\textbf{e}_{1}$, $\textbf{e}_{2}$ a $\textbf{e}_{3}$ pak definují pravotočivý souřadný systém. Vodiči protékají elektrické proudy $I_{1}$ a $I_{2}$. Velikost proudů je kladná, pokud mají směr $\textbf{e}_{3}$. Pomocí transformačních vztahů pro elektrické a magnetické pole ukažte, že první vodič působí na úsek délky $l$ druhého vodiče silou

$\textbf{F}_{l}$ = $– \mu_{0} ⁄ (2\pi)$ $\cdot (I_{1}I_{2}l⁄r)$ $\textbf{e}_{1}$.

K řešení této úlohy užijte následující poznámky. Kovy jsou tvořeny krystalovou mřížkou kladně nabitých iontů, mezi nimiž se pohybují volné elektrony. (Toto je velmi zjednodušený model struktury kovů. Nicméně pro náš problém je postačující.) Pokud ke kovu přiložíme vnější elektrické pole, potom se volné elektrony začnou pohybovat proti směru elektrické intenzity. Tím v kovu vzniká elektrický proud. Rychlost uspořádaného pohybu elektronů je při běžných hodnotách proudu velmi malá, méně než metr za sekundu.

Elektrostatické pole homogenně nabité přímky s délkovou hustotou náboje $\lambda$ je ve vzdálenosti $r$ od zdroje popsáno elektrickou intenzitou o velikosti $E = \lambda / (2\pi\epsilon_{0}r)$. Vektor elektrické intenzity vždy leží v rovině kolmé na přímkový zdroj a jeho směr udává přímka procházející zdrojem a bodem, ve kterém nás zajímá hodnota elektrického pole. Vektor elektrické intenzity směřuje od zdroje, je-li zdroj nabit kladně. Tento výsledek lze získat sečtením (integrací) příspěvků od jednotlivých elementů přímkového zdroje. Příspěvek elementu zdroje je dán Coulombovým zákonem. Další možností je v tomto případě užití Gaussovy věty, neboť směr elektrické intenzity plyne ze symetrie.

Z Maxwellových rovnic plyne pro rychlost světla ve vakuu vztah $c^{2} = 1/\epsilon_{0} \mu_{0}$. O platnosti tohoto vzorce se lze snadno přesvědčit dosazením tabulkových hodnot příslušných fyzikálních konstant.

Máme žárovku, která svítí na výkonu $100 \,\jd{W}$. Chceme vyrobit žárovku pro výkon $60 \,\jd{W}$ a použít přitom stejný materiál vlákna. Chceme, aby obě žárovky svítily „stejně“ (měly stejnou spektrální vyzařovací charakteristiku). Jaké rozměry musí mít vlákno v $60 \,\jd{W}$ žárovce vzhledem k tomu ve $100 \,\jd{W}$?

Máme $50\, \jd{kg}$ mědi. Jaký nejdelší drát z tohoto množství materiálu lze vytvořit pro přenášení elektrického proudu $1 \jd{A}$, je-li okolní teplota $20\jd{^{\circ}C}$? (Tepelnou kapacitu okolního vzduchu a přírody považujte za nekonečnou.)

Mějme nekonečný drát stočený do pravotočivé šroubovice (helixu). Drát je rovnoměrně nabitý a osa helixu je totožná s osou $z$. Do vzniklého pole pošleme nabitou částici (drát je tenký, takže do něj částice nenarazí). V jistém časovém okamžiku známe její $p_{z}$ a $L_{z}$, tedy $z$ové komponenty hybnosti a momentu hybnosti. Můžeme v jiném okamžiku určit $p_{z}$, známe-li v tomto okamžiku $L_{z}?$

(Problém lze vyřešit zcela exaktně. Naproti tomu není určitě nezajímavé zkusit situaci počítačově simulovat a dostat tak hledanou závislost v podstatě experimentálně, v případě ověřit teoretickou předpověď.)

Do kapalného dielektrika jsou svisle ponořeny dvě čtvercové paralelní vodivé desky o straně $a$. Nejsou-li desky nabity, vystoupí hladina mezi deskami do výšky $h_{0}$ (měřeno od dolního okraje desek). O jakou vzdálenost $\Delta h$ se zvýší hladina kapaliny mezi deskami, nabijeme-li desky na napětí $U$? Permitivita kapaliny je $\epsilon$, hustota $\rho$ a vzdálenost desek je $d$ ($d << a$).

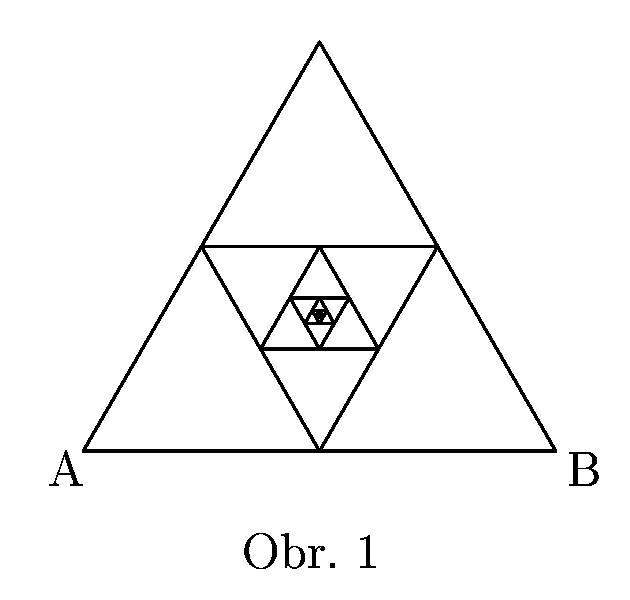
Mějme drát, jehož jednotka délky má odpor $R$. Z rovnostranných trojúhelníků z něj vyrobených postavíme nekonečnou síť naznačenou na obrázku (nejdelší strana má jednotkovou délku). Jaký odpor bude mezi vrcholy největšího trojúhelníku?

Uvažujte tranzistor JFET vyrobený z polovodiče typu N ve tvaru kvádru o hranách $a$, $b$, $c$. Na dvou protilehlých stěnách jsou vývody S a D, na jiných dvou protilehlých je z polovodiče typu P vývod G (obě stěny jsou vodivě propojeny na jeden vývod). Předpokládejme, že šířka přechodu je dána vztahem $d=d_{0}+λU'$, kde $U'$ je závěrné napětí. Předpokládejme navíc, že proud může procházet pouze oblastí polovodiče N mimo přechod. Proud tekoucí polovodičem se stanoví ze vztahu $I=SσU⁄l$, kde $U$ je napětí mezi svorkami na polovodiči s vodivostí $σ$, jejichž vzdálenost je $l$ a proud prochází kolmo plochou $S$. Z tohoto jednoduchého modelu se pokuste stanovit závislost proudu tranzistorem na napětí mezi svorkami S a D, jako parametr uvažujte napětí na svorce G. Úlohu si ještě můžete zpestřit porovnáním výsledku s charakteristikou válcového tranzistoru JFET, kde je polovodič P po celém plášti válce.

Proveďte diskusi funkce PNP tranzistoru. Porovnejte s funkcí NPN tranzistoru kvalitativně, ale i kvantitativně. Díra má stejný náboj jako elektron, má však menší pohyblivost. Co se stane, když posvítíme dovnitř tranzistoru (PNP i NPN)?

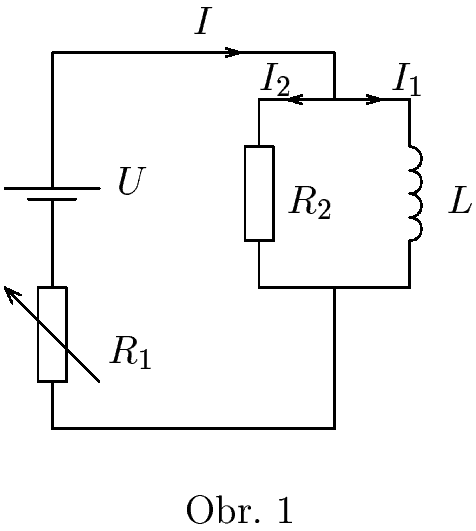
Mějme následující obvod (viz. obrázek). Část obvodu obsahující $R_{2}$ a $L$ $(10\,\jd{H})$je ponořena do kapalného hélia. Vodiče v této části jsou supravodivé (mají nulový odpor). Vyndáme-li $R_{2}$ z hélia, má odpor $5 \,\jd{Ω}$.

První experiment probíhá následovně: Proud $I$ měníme pomocí $R_{1}$ tak, aby v časovém intervalu $(t_{0},t_{1})$ byl konstantní $1 \,\jd{A}$, v $(t_{1},t_{2})$ rovnoměrně klesal na nulu, v $(t_{2},t_{3})$ rovnoměrně stoupal na $0,5 \,\jd{A}$ a dále byl konstantní. V čase $t_{3}$ rezistor $R_{2}$ vyndáme z hélia a v čase $t_{4}$ jej tam opět spustíme. V $t_{0}$ je $I_{1}=I_{2}=0,5 \,\jd{A}$. Určete časový průběh $I_{1}$ a $I_{2}$ v časovém intervalu ($t_{0},t_{4})$.

Druhý experiment probíhá následovně: Na počátku je $R_{2}=0 \,\jd{Ω}$, $I_{1}=0 \,\jd{A}$, $R_{1}=7,5 \,\jd{Ω}$, $I=0,5 \,\jd{A}$. $R_{1}$ se dále nemění. V čase $t_{1}$ vyndáme $R_{2}$ z hélia a v čase $t_{2}$ jej tam opět spustíme. Načrtněte do grafu průběh časové závislosti $I$, $I_{1}$, $I_{2}$.