Vyhledávání úloh podle oboru
Databáze úloh FYKOSu odjakživa
astrofyzika (85)biofyzika (18)chemie (24)elektrické pole (71)elektrický proud (76)gravitační pole (81)hydromechanika (146)jaderná fyzika (44)kmitání (57)kvantová fyzika (31)magnetické pole (43)matematika (89)mechanika hmotného bodu (298)mechanika plynů (87)mechanika tuhého tělesa (221)molekulová fyzika (72)geometrická optika (78)vlnová optika (65)ostatní (167)relativistická fyzika (37)statistická fyzika (21)termodynamika (155)vlnění (51)
hydromechanika
4. Série 12. Ročníku - 3. tyč ve vodě
Tyč o hustotě $ρ_{1}$ a délce $l$ je za jeden konec pohyblivě připevněna k vodorovné hrazdě (tak, že se okolo ní může tyč volně otáčet), druhý konec volně visí. Pokud budeme pomalu spouštět hrazdu dolů, bude se tyč přibližovat k hladině vody ($ρ>ρ_{1}$) a začne se do ní ponořovat. Zjistěte závislost úhlu, který svírá tyč se svislým směrem, na výšce hrazdy nad hladinou.
2. Série 12. Ročníku - 2. přehrada

Na řece je postavena přehrada. Plocha umělého jezera je $100\, 000\,\jd{ m^{2}}$, voda z přehrady je vypouštěna stavidlem, které si můžeme představit jako ocelovou desku širokou $l=20\;\mathrm{m}$ a vysokou $h=10\;\mathrm{m}$, která, když přehrada nevypouští žádnou vodu, sedí na betonové konstrukci (viz obrázek). Když chceme vodu vypouštět, stavidlo zvedneme a voda poteče mezi dolní stranou stavidla a betonovou konstrukcí přehrady. Běžný průtok přehradou je $20\,\jd{ m^{3}\cdot s^{-1}}$, průtok větší než $100\,\jd{ m^{3}\cdot s^{-1}}$ je považován za povodeň.
Předpokládejme tuto situaci: Kvůli plnému energetickému využití je přehrada zcela naplněna vodou ($y=10m$), přitéká i odtéká $20\,\jd{ m^{3}\cdot s^{-1}}$ vody. Náhle (v čase $t_{0})$ se obsluha přehrady dozví neradostnou zprávu, že se blíží povodňová vlna – za tři hodiny se přítok najednou zvýší na $200\,\jd{ m^{3}\cdot s^{-1}}$ a tento stav potrvá další tři hodiny. Poté se přítok opět sníží na $20\,\jd{ m^{3}\cdot s^{-1}}$. Obsluha má za úkol zabránit povodni pod přehradou. Nalezněte funkci $f(t)$, která popisuje závislost velikosti zvednutí stavidla na čase v intervalu $(0\,\jd{h};6\,\jd{ h})$ tak, aby k povodni pod přehradou nedošlo. Pokud povodni zabránit nelze, stanovte maximální výšku vody $y_{max}$ v čase $t_{0}$, pro kterou je ještě možno zabránit povodni a určete funkci $f(t)$.
2. Série 12. Ročníku - 3. vodní lyže
Vaším úkolem je přijít na to, jak fungují vodní lyže. Proč lyžař neklesne ke dnu? Proč je jeho pozice poměrně stabilní?
1. Série 12. Ročníku - 1. srdce
Lidské srdce napumpuje za minutu $q=5\,\jd{l}$ krve při tlaku $p=100\;\mathrm{mm}Hg$. Kolik dní by byla schopna konat stejnou práci standardní autobaterie s účinností $\eta=50%?$ ($Q=48\,\jd{Ah}$, $U=12\,\jd{V}$).
1. Série 12. Ročníku - 3. fontána
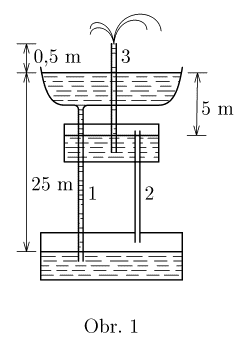
Fontána
Na obrázku je nakreslen důmyslný systém nádržek. Spočtěte rychlost vody vystřikující z trubky 3. Viskozitu vody zanedbejte.
6. Série 11. Ročníku - E. akvárium
Najděte si akvárium, nebo podobnou nepropustnou nádobu kvádrového tvaru a zčásti ji naplňte vodou do výšky $h$. Nádobou rychle pohněte ve směru jedné ze stěn, aby hladina začala kmitat tak, jak je to naznačeno na obrázku. Změřte frekvenci, s kterou hladina kmitá, proveďte pokud možno více měření pro různé hodnoty $h$ a $l$ a výsledky se pokuste interpretovat (vymyslete fyzikální model). Omezte se na malé amplitudy kmitů.
4. Série 11. Ročníku - 2. vodní hodiny
Vodní hodiny jsou přesýpací hodiny, ve kterých se místo přesypávání písku přelévá voda. Navrhněte jejich tvar tak, aby hladina vody v horní nádobce klesala konstantní rychlostí. Vzduch je z nádobek vyčerpán.
4. Série 11. Ročníku - P. levitující kapalina
Jistě jste si už někdy všimli, že když vytahujeme skleničku z umyvadla dnem vzhůru, zůstává v ní voda až do té chvíle, kdy její okraj vytáhneme nad hladinu. Pak všechna vyteče. Vysvětlete proč. Uvědomte si, že na povrch kapaliny ve skleničce obrácené dnem vzhůru působí tlak vzduchu, který dokáže vytlačit až deset metrů vodního sloupce!
1. Série 11. Ročníku - 4. grant strýčka Skrblíka
Zlepsovak 1
Strýček Skrblík se jednou doslechl o perpetuech mobile a vytušil příležitost, jak ještě více zbohatnout. Vypsal grant na vymýšlení „věčných strojů“, ale jediní, kdo se přihlásili, byli jeho synovci. Přinesli strýčkovi následující tři nápady:
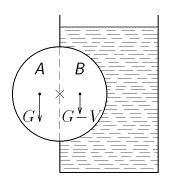
- Základem prvního perpetua je válec, který je dutý, vodotěsný a je upevněn v ose na valivých ložiscích. Obrázek nám objasní funkčnost stroje. Na obě části válce sice působí tíhová síla $G$, ale část $B$ je vůči části $A$ válce nadlehčována vztlakovou silou $V$ dle Archimédova zákona. Válec se bude otáčet a jeho rotační energii převedeme na elektrickou energii.
- Pokud zahřejeme kapalinu, zvětší svůj objem. Zároveň víme, že kapalina je nestlačitelná. Proto budeme kapalinu zahřívat a ochlazovat, změnu jejího objemu převedeme na mechanickou energii a tu na energii elektrickou. Část takto obdržené energie využijeme na zahřívání kapaliny (ochlazení kapaliny zajistí okolní prostředí, odborně „lázeň“). Zbytek energie roztočí stroje ve Skrblíkových továrnách.
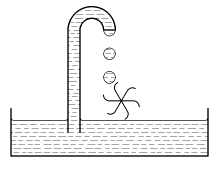
* Do nádoby s vodou je zasunuta kapilára. Díky kapilárním jevům voda naplní celou kapiláru a z horního zahnutého konce odkapává dolů, jak je to vidět na obrázku. Dole je umístěna vodní turbína, která je roztáčena padající vodou, a tak může konat práci.
Strýček se nadšeně pustil do výroby těchto strojů, jaké však bylo jeho zklamání, když zjistil, že ani jediný z nich nefunguje. Od té doby už o žádných „perpetech“ nechce ani slyšet.
Na vás teď je, drazí řešitelé, abyste se pokusili vysvětlit, proč žádný z nápadů synovců strýčka Skrblíka nemůže fungovat jako perpetuum mobile.
6. Série 10. Ročníku - P. vodovod
Ke koncům vodorovné trubice délky $l$, hmotnosti $M$ a konstantního průřezu $S$ jsou připevněna kolena, která přivádí vodu seshora a odvádí ji směrem dolů (voda běží svisle, zatočí doleva a běží vodorovně a pak zahne vpravo a běží zase svisle dolů). Druhé koleno je upevněno na otočném kloubu. Jaký průtok musí být v trubici, aby se netočila?