Vyhledávání úloh podle oboru

Lidský vlas má u některých lidí tendenci zaujmout zakroucený tvar. Uvažujme vlas, který má v klidovém stavu dané parametry podobně jako stočená pružinka (poloměr, sklon, materiálové konstanty). Spočítejte, jak se vlas prodlouží, když ho nejprve položíme vodorovně na stůl a potom ho pověsíme svisle dolů. Uvažujte hodně stočený vlas, tj. s malým sklonem.

• napnutá struna

Frekvence kmitů napjaté struny závisí na její délce $l$, síle $F$, kterou je struna napjatá, a na délkové hustotě $ρ_{l}$. Určete z těchto údajů vzoreček pro frekvenci struny pomocí rozměrové analýzy.

• dolů

Mějme činku, jejíž závaží mají tvar disků, které jsou blízko u sebe. Tyčku omotáme jednou provázkem a činku spustíme, jak rychle padá, pokud se nesmýká? Disky mají hmotnost $m$ a poloměr $R$, tyčka je nehmotná s poloměrem $r$.

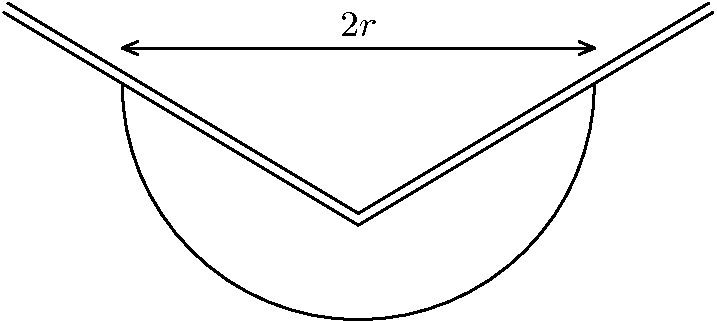
Uvažujme misku o poloměru $r$, do které položíme dvě spojená brčka, která mají tvar písmene V. Brčko se smí dotýkat pouze okrajů misky. Určete nejprve podmínku stability a potom vypočítejte periodu kmitů brčka v souměrné poloze.

Ve starém gauči našel Lukáš pružinu o tuhosti $k$, poloměru závitu $r$, délky $l$ a počtem závitů $n$. Protože se nudil, připojil ji ke stabilnímu zdroji elektrického proudu $I$. Jak se změnila její tuhost?

Jak rychle máme jít po visutém mostě, abychom jej co nejvíce rozkmitali? Úlohu vhodně parametrizujte a následně vyřešte.

Prodává se váleček, na kterém jsou malé výstupky. Váleček otáčeje se brnká o hranu ocelové destičky, která je nařezaná na proužky rozdílné délky. Ve skladbě na válečku se vyskytují všechny noty v daném neprázdném rozsahu (dejme tomu stupnice C dur). Dokážete zjistit tvar funkce konců nařezaných proužků?

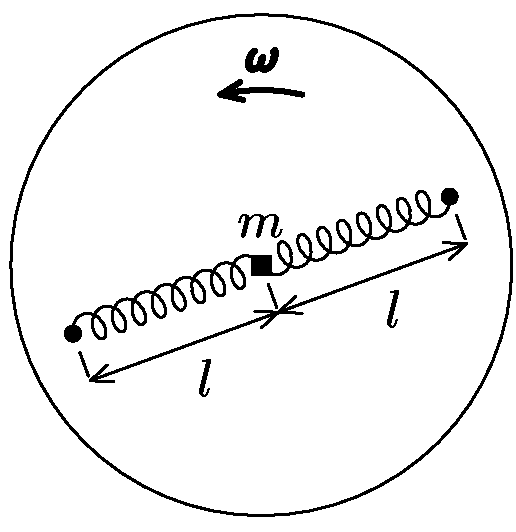
Kutil Mára si doma sestavil takovouto hračku: Na dřevěný kruh do jedné přímky procházející středem disku přimontoval dvě zarážky (stejně daleko od středu), mezi které na dvou pružinách o tuhosti $k$ napnul závaží o hmotnosti $m$. Závaží může bez tření klouzat po disku. Mára hračku položil na stůl a roztočil okolo osy disku úhlovou rychlostí $ω$, přičemž závaží mírně vychýlil z rovnovážné polohy. Kvalitativně popište pohyb závaží, a pokud si věříte, vypočítejte jej (za bonusové body).

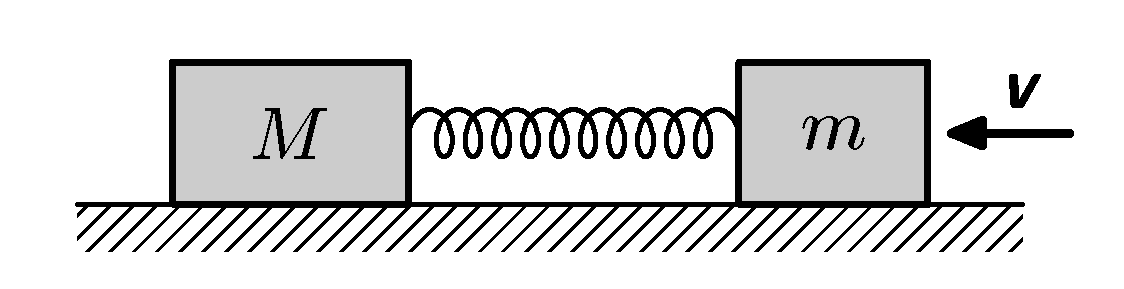
Dvě závaží o hmotnostech $m$ a $M$ jsou spojena pružinou o tuhosti $k$ a leží na hladké podložce (tření můžeme zanedbat). Tělesu $m$ udělíme rychlost $v$ (viz obrázek). Jaká bude nejkratší vzdálenost mezi tělesy a kdy jí dosáhnou?

Kačenka se rozhoupává na houpačce následujícím způsobem. Při největší výchylce houpačky se přikrčí, a když je houpačka v nejnižším bodě, opět se postaví. Tyto pohyby neustále opakuje. Poměr vzdálenosti těžiště Kačenky od osy otáčení při pokrčení a při stání je $2^{1⁄12} ≈ 1,06$. Kolikrát se Kačenka zhoupne, než se amplituda houpání zdvojnásobí?

Na zámořském parníku připravuje pro posádku jídlo kuchař Thomas. Na podávání talířů má šikovné zařízení. Pružinový držák udržuje vrchní talíř pořád ve stejné výšce. Vzdálenost mezi talíři je 1 cm. A protože je moře bouřlivé, sloupec 25 talířů pěkně kmitá. Jaká je frekvence těch kmitů?