Vyhledávání úloh podle oboru
Databáze úloh FYKOSu odjakživa
astrofyzika (85)biofyzika (18)chemie (24)elektrické pole (71)elektrický proud (76)gravitační pole (81)hydromechanika (146)jaderná fyzika (44)kmitání (57)kvantová fyzika (31)magnetické pole (43)matematika (89)mechanika hmotného bodu (298)mechanika plynů (87)mechanika tuhého tělesa (221)molekulová fyzika (72)geometrická optika (78)vlnová optika (65)ostatní (167)relativistická fyzika (37)statistická fyzika (21)termodynamika (155)vlnění (51)
mechanika hmotného bodu
1. Série 8. Ročníku - 4. setrvačnost
V autobuse (jede z pouti a má zavřené nejen dveře, ale i okna) stojí cestující a drží na provázku svůj balónek plný helia. Autobus, který původně stál v klidu, se rozjíždí. Co se stane s balónkem? (Cestující je pevně spojen s autobusem –tj. dobře se drží.) Jakým směrem se balónek pohne? Vysvětlete souvislost se setrvačnou silou! Můžete si to také vyzkoušet.
1. Série 8. Ročníku - E. bungee-jumping
Zajisté jste slyšeli o novém druhu zábavy lidí, kteří si potřebují dokázat, jak snadné je překonat vlastní strach. Z vlastní vůle skočit z výšky třeba $50\; \textrm{m}$ přivázán jen za nohy, není to lákavé? Vaším úkolem by mělo být: laboratorně zkoumat dynamiku tohoto nového sportu (kdy se asi dostane do olympijských her?) a na základě pokusů domácky provedených učinit závěry z toho plynoucí pro člověka přivázaného na takovém laně.
Nejprve si obstaráte kus gumy přiměřené délky. Pak můžete měřit:
- závislost maximální hloubky $h$ na délce gumy $l$, do níž se závaží hmotnosti $m$ klesne
- závislost hloubky $h$ na hmotnosti závaží $m$ pro dvě různé délky gumy $l_{1}$, $l_{2}$. Pozor abyste nepřekročili kritickou hmotnost $M_{K}$ z bodu $c$!
- jaká je kritická hmotnost $M_{K}$ závaží, při němž se guma délky $l$ přetrhne (tento úkol předpokládá, že máte dost experimentálního materiálu a máte též vhodnou gumu – zachovává pružné vlastnosti až do přetržení)
Pro člověka vysícího na takovém laně má značný význam maximální zrychlení na něj působící po čas letu. Pokuste se toto zrychlení určit na základě změřených výsledků.
Přejeme Vám mnoho úspěchů při řešení a hodně zábavy s praskající gumičkou!
6. Série 7. Ročníku - P. redundantní informace
Z Prahy vyjíždí v 7 hodin 30 minut rychlostí 95 km/h po dálnici do Brna černý, pečlivě umytý automobil Tatra 613, ve kterém sedí na zadním sedadle za řidičem bílý pták, velký jako pštros, ale s dlouhým a silným žlutým zobákem. Přibližně každých pět minut pták klovne řidiče do hlavy. Ten si toho sice většinou nevšímá, ale čas od času se rozzuří, popadne složené noviny, které leží na prázdném předním sedadle, zakloní se, levou rukou drží volant a pravou tluče novinami ptáka přes hlavu a křičí: „Nech už toho, ty kreténe! Ty máš opravdu ptačí mozek!“ Pták se krčí na zadním sedadle a ustrašeně vřeští, ale za pět minut klovne řidiče znovu.
Téhož dne v 8 hodin 15 minut vyjíždí z Brna do Prahy rychlostí 70 kilometrů za hodinu kamión s tureckou poznávací značkou. Neveze žádné zboží, v jeho vnitřku se nachází pouze pětačtyřicetiletý docent estetiky B. Je na zadním konci kamiónu připoutaný ke klice dveří a dívá se na divný film, promítaný na plátně, jež je umístěné na druhém konci vozu. Vidí ve filmu sám sebe, jak leží v noci ve své vile s manželkou v posteli a spí; manželka tiše vstává z postele a sestupuje do zahrady, kde na ni vzadu u plotu čekají fantastické nestvůry, jsou to tlusté žáby, velké jako pes, porostlé dlouhou vlnitou srstí, s losími parohy na hlavě a s velkými chlupatými křídly. Na špičkách paroží svítí Eliášův oheň. Žáby obletují ženu, která tu tiše stojí v bílé noční košili, dlouhé chlupy na křídlech jim přitom krásně vlají, olizují ženě jazykem tvář a kňučí radostí jako psi. Žena je něžně hladí po hlavě a tiskne je k sobě, pak se temnou zahradou rychle vrací do vily a uléhá opět do postele. Letos je tomu 20 let, co se docent B. se svou manželkou vzali.
Z Prahy do Brna je to po dálnici 202 km. V kolik hodin a na kolikátém kilometru se oba automobily minou?
Michal Ajvaz: Návrat starého varana, MF, Praha 1991, str. 50–51.
4. Série 7. Ročníku - 1. vláček
Dlouhá vlaková souprava délky $l$ jede po dráze, která z vodorovného úseku přechází ve svah se sklonem $a$. V okamžiku, kdy se vlak zastavil, byla na svahu přesně polovina vagónů. Jaká byla doba, za kterou vyjely tyto vagóny na svah. Tření zanedbejte.
4. Série 7. Ročníku - 2. kužel
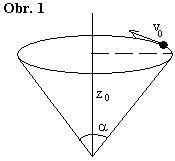
Hmotný bod se v tíhovém poli Země pohybuje po vnitřku kuželové plochy s vrcholovým úhlem $2α$, jejíž osa symetrie má svislý směr (viz obr. 1). V čase $t=0$ se částice nachází ve výšce $z_{0}$ a má rychlost $v_{0}$. Tato rychlost má směr tečny ke kružnici na průniku kužele s vodorovnou rovinou $z=z_{0}$.
- Obíhá-li částice v konstantní výšce $z_{0}$, dokažte, že velikost rychlosti je určena pouze touto výškou a nezávisí na úhlu $α$.
- Při obecném pohybu určete body obratu $z_{1}$ a $z_{2}$, tj. maximální a minimální výšku, do které částice vystoupí.
Diskutujte trajektorii částice v soustavě spojené s částicí a soustavě spojené se Zemí. Tření neuvažujte.
2. Série 7. Ročníku - P. závodník
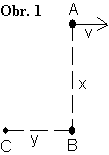
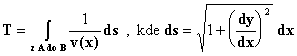
V důsledku malého koeficientu tření pneumatik se automobil jedoucí po ledu nemůže pohybovat se zrychlením větším než $a=0,5\;\mathrm{m}\cdot \mathrm{s}^{-2}$. Podle pravidel závodu se řidič musí dostat z bodu A do B ve vzdálenosti $x=375\;\mathrm{m}$, přičemž počáteční rychlost $v=10\;\mathrm{m}\cdot \mathrm{s}^{-1}$ jest ve směru kolmém ke spojnici AB. Určete nejmenší čas, za který toho lze dosáhnout. Jak se změní výsledek, bude-li cílem bod C (viz obr. 1), vzdálenost B a C je $y=200\;\mathrm{m}$.
1. Série 7. Ročníku - 4. korálek
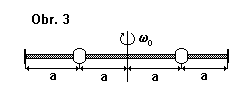
Na tyči zanedbatelné hmostnosti o celkové délce $4a$ jsou navlečeny ve vzdálenosti $a$ od osy otáčení dvě koule o hmotnosti $m$ (viz obr. 3). Na obou koncích tyče jsou umístěny dokonale pružné odrazné destičky. Tyč je roztočena na úhlovou rychlost $ω_{0}$, a poté jsou uvolněny obě koule. Za předpokladu, že se tyč nadále pohybuje volně a bez tření, určete:
- Po jaké trajektorii se budou pohybovat obě kuličky vzhledem k pozorovateli v inerciální soustavě.
- Jak se bude měnit úhlová rychlost soustavy $ω$ v závislosti na čase.
- Jak by se změnili výsledky předešlých úloh, kdybychom udržovali (např. pomocí motoru) úhlovou rychlost stále na hodnotě $ω_{0}?$
1. Série 7. Ročníku - P. fošna
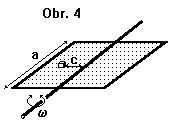
Čtvercová deska o straně délky $a$ (viz obr. 4) je upevněna na ose procházející jejím středem ve směru rovnoběžném s jednou ze stran. Ve vzdálenosti $c$ od této osy je na ní položeno malé tělísko hmotnosti $m$. Deska začne kmitat s nevelkou amplitudou kolem vodorovné polohy s frekvencí $ω$. Určete dobu (je mnohem větší než perioda kmitů), za kterou tělísko spadne z desky, je-li koeficient tření mezi deskou a tělískem $μ$.
5. Série 2. Ročníku - 1. závažíčko na kouli
Na vrcholu koule poloměru $R$ leží závažíčko, které se v čase nula začne pohybovat. V jaké výšce a kdy se oddělí od povrchu koule?
4. Série 2. Ročníku - 1. vozík
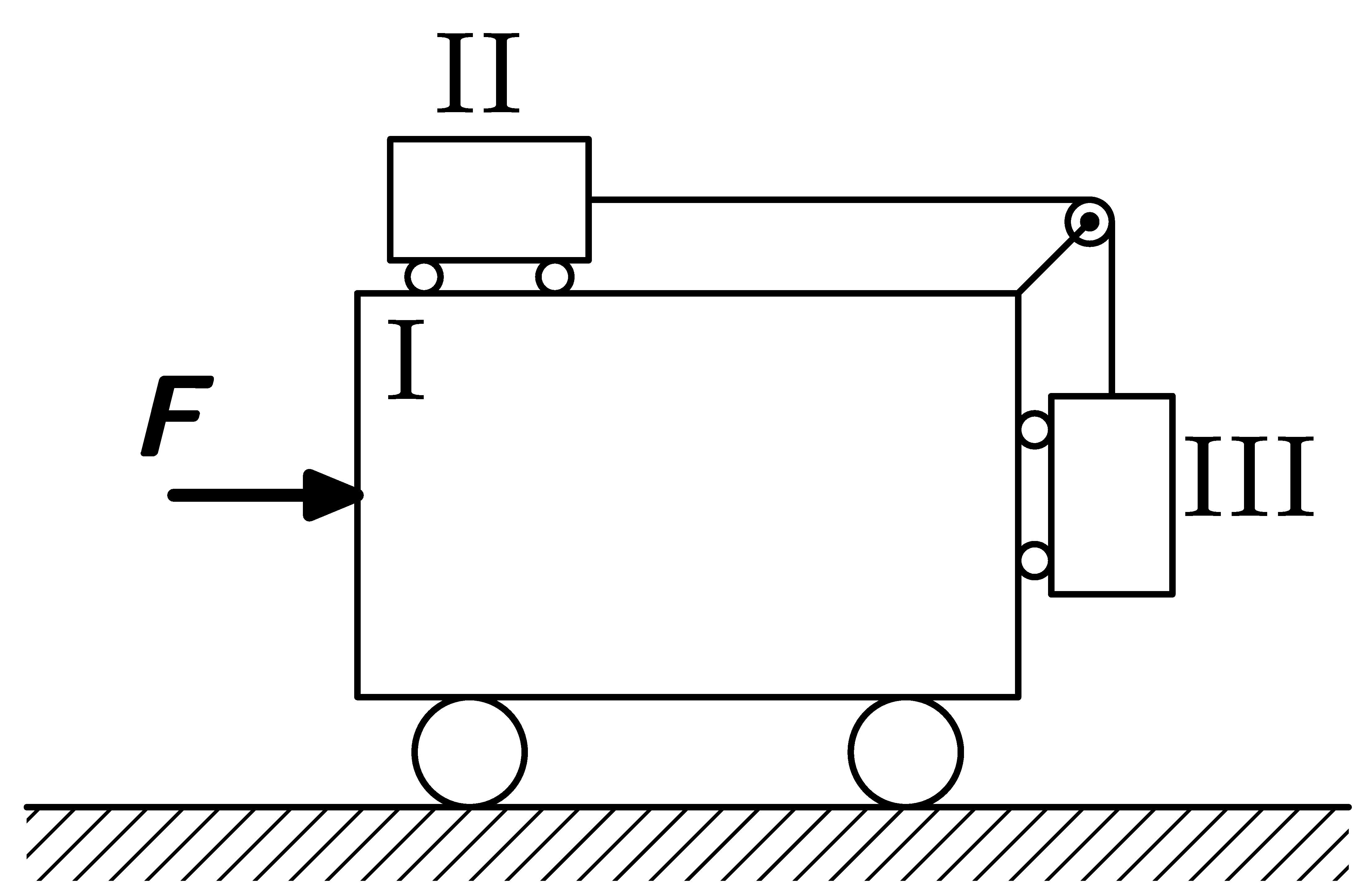
Model tří těles
Mějme soustavu vyobrazenou na obrázku. Jakou silou $\textbf{F}$ musíme působit, aby se těleso II nepohybovalo vůči tělesu I. Máte zadané hmotnosti $m_{I}$, $m_{II}$ a $m_{III}$ všech tří těles a veškerá tření zanedbávejte.