Vyhledávání úloh podle oboru

• Co se stane, když do krystalu kalcitu kolmo posvítíme kruhově polarizovaným světlem?
• Představte si, že je právě čas $t=0$, široko daleko není žádný náboj

($ρ=\textbf{j}=0)$, a my známe počáteční elektromagnetické pole v celém prostoru $\textbf{E}(\textbf{r},0)$ a $\textbf{B}(\textbf{r},0)$. Z rovnic (14) a (15) tedy můžeme vyjádřit časové derivace $∂\textbf{B}⁄∂t$ a $∂\textbf{E}⁄∂t$ pomocí prostorových a vypočítat tak $\textbf{E}$ a $\textbf{B}$ v následujícím okamžiku. Tento postup můžeme iterativně opakovat a dostat tak celý časový vývoj pole pro $t>0$. Jak je možné, že vůbec nemusíme použít první a druhou Maxwellovu rovnici?

• Uvažujte náboj velikosti $q$, který je v klidu pro $t\lt0$, a v čase $t=0$ na něj začne dopadat rovinná světelná vlna. Jak se bude náboj následně pohybovat, když světlo je polarizované (i) lineárně (ii) kruhově? Promyslete nejprve kvalitativně, přesný výpočet, případně počítačová simulace obdrží bonus.

Jak nejdále od sebe mohou být dva lidé, aby je nikdo třetí na Zemi nerozeznal, kdykoliv jsou viditelní? Nezapomeňte, že lidé jsou bodové světelné zdroje ve výšce 2 m a Země je koule.

Jak roste hlasitost (definujte si sami) sboru s počtem jeho členů? Co z toho plyne? Členy sboru uvažujte jako bodové zdroje zvuku stejné amplitudy a frekvence, ale posunuté o náhodnou fázi. Všichni bodoví zpěváci se nacházejí v jednom místě.

• V textu seriálu jsme pracovali s diskrétním rozložením bodových zdrojů na přímce a jejich zobrazením na přímku. Nyní si představte, že máte zdroje světla rozložené na rovině a stínítko je rovina na ni rovnoběžná. Popište rozložení intenzity na stínítku v případě, že zdroje světla:

• Leží na jedné přímce s pravidelným intervalem $d$.

• Jsou rovnoběžné přímky, kde vzdálenost mezi sousedními přímkami je $d$.

• Leží ve vrcholech obdélníkové sítě, kde obdélníky mají strany $a$, $b$.

• Mějme následující situaci: Před stínítkem, reprezentovaném nějakou rovinou $xy$ je disk o poloměru $R$, rovnoběžně s rovinou. Ze strany disku na stínítko svítíme z nekonečna světlem, tzn. všechny paprsky jsou navzájem rovnoběžné

a kolmé na rovinu $xy$. Vysvětlete, proč situaci můžeme popsat pomocí bodových zdrojů světla spojitě rozložených všude na rovině ve které leží disk kromě disku samotného, najděte závislost intenzity světla na rovině $xy$ jako funkci $x$ a $y$ (není potřeba uzavřený tvar, stačí ve tvaru integrálu) a ukažte, že v bodě, který je na rovině $xy$ přímo naproti středu disku se děje něco, co bychom z hlediska geometrické optiky nečekali.

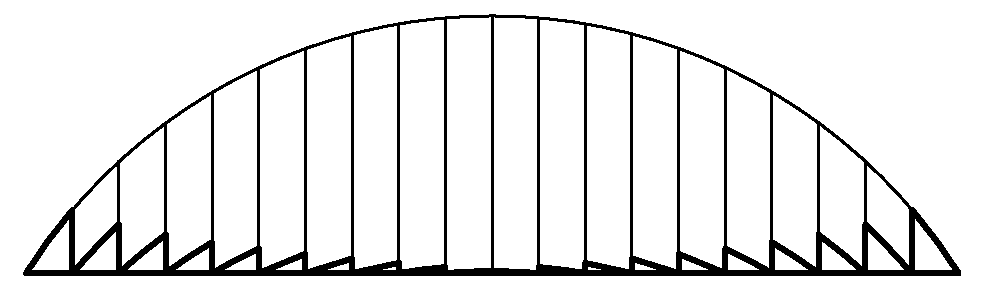
Možná jste si všimli, že mezi zdrojem a průhlednou podložkou na fólie je v tradičním meotaru za účelem soustředění světla vložená dost zvláštní čočka, která vypadá spíš jako rýhovaná deska (viz také úloha VI.2 ze XVII. ročníku). Vznikne tak, že standardní ploskovypuklou čočku rozřezáme na soustředné prstence, z každého si necháme jen úplný konec a výsledek opět složíme, takže získáme něco jako „osově symetrické pahorkaté sklo“ (viz obrázek).

Takto vzniklá čočka má všude stejný sklon jako původní spojka, a podle Snellova zákona tak očekáváme, že bude stejně dobře soustřeďovat světlo. Naproti tomu, z pohledu Fermatova principu, už každé dráze nepřísluší stejný čas, neboť jsme v různých místech odebrali různě tlusté vrstvy skla – například úplně nejkratší čas teď odpovídá cestě po optické ose. Zdá se tedy, že Fermatův pricnip selhává – podle něj by čočka soustřeďovala jen světlo jdoucí po optické ose a nefungovala tak, jak má. Rozhodněte kdo má pravdu: Snell, Fermat? A proč?

• Najděte dráhy paprsků ve dvojrozměrné situaci, kdy závislost indexu lomu na vzdálenosti $r$ od počátku je dána funkcí

$n(r)=n_{0}⁄(1+(r⁄a))$.

• Bonus: Vložíme-li do prostoru s proměnlivým indexem lomu bodový zdroj světla,

může se stát, že se velká část paprsků, které z něj vycházejí, sejde v jednom bodě, jako je tomu v případě spojné čočky. Takto vzniklý bod pak nazýváme obrazem bodu původního. Popište geometrické zobrazení $zdroj→obraz$, které tímto způsobem indukuje prostředí s indexem lomu z předchozí úlohy.

• Co uvidí člověk stojící mezi dvěma spojenými na sebe kolmými zrcadly, jejichž spojnice je svislá?

• Mějme rovinné zrcadlo skloněné pod úhlem 45°, pohybující se zleva doprava rychlostí $v$. Zprava na něj dopadá paprsek světla rychlostí $c$ (úhel dopadu je tedy 45°) a odráží se zhruba nahoru. Pomocí Huygensova principu určete úhel mezi dopadajícím a odraženým paprskem, tedy vlastně opravte zákon odrazu a dopadu pro pohybující se zrcadlo.

1. Představte si, že vezmete dostatečně silný laser, vyzařující světlo vlnové délky $400\, \jd{nm}$, a posvítíte s ním na Měsíc. Od jeho povrchu se vyzářené světlo odrazí a vrátí se zpět. Předpokládáme-li, že laser vyzařuje skrze kruhový otvor průměru $1\, \jd{cm}$, jaký bude na zemském povrchu průměr paprsku navracejícího se po odrazu zpět? Poradíme vám, že to bude o poznání více, než $1\, \jd{cm}$.
2. V této úloze předpokládejte, že éter skutečně existuje a předpovězte, jak by to dopadlo, kdyby Michelson prováděl svá měření jiným způsobem: Jedno rameno by nechal dlouhé $5$ metrů, zatímco druhé by bylo dlouhé $10\, \jd{m}$. Takto připravená aparatura by vytvořila nějaký interferenční obrazec. Poté by Michelson celou soustavou otočil o $90^{\circ}$, takže by si obě ramena vyměnila místa. V průběhu tohoto otáčení by docházelo k posunům interferenčních proužků. (Představte si rotující dvojštěrbinu.) Jak by se v uvedené aparatuře posunuly interferenční proužky při naznačené rotaci? Jak dlouhé by muselo být delší rameno, aby se interferenční proužky vyměnily, tedy aby se rotací maxima posunuly na minima?
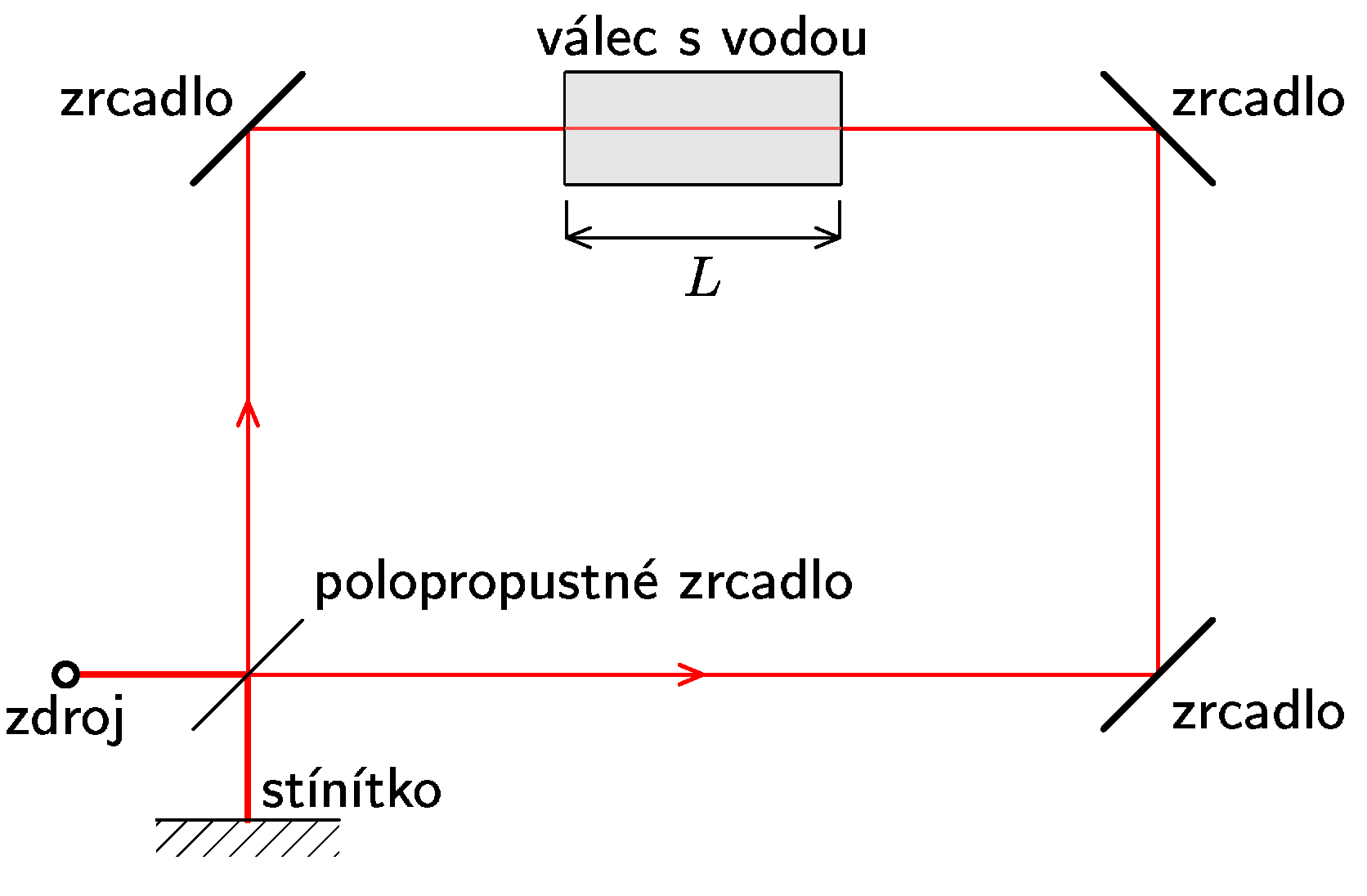
3. V následující úloze předpokládejte, že éter existuje a že těleso pohybující se v éteru jej úplně strhuje, takže relativní rychlost tělesa vůči éteru je nulová. Jaký fázový posun by poté vznikl mezi dvěma paprsky v soustavě, naznačené na obrázku? Světlo ze zdroje se na polopropustném zrcadle rozdělí na dva svazky a pokračuje po dokonale obdélníkové dráze zpět na polopropustné zrcadlo, kde vystupuje na stínítko, na kterém sledujeme interferenční proužky. Po cestě jsou oba paprsky třikrát odraženy na zrcadle a procházejí válcem délky $L$, naplněným vodou. Celá soustava kromě válce s vodou (ten je vůči éteru v klidu, nezapomeňte) se vůči éteru pohybuje rychlostí $v$ směrem vpravo.

Přispějte něčím zajímavým do deníku vědecké výpravy (obrázkem či jiným uměleckým výtvorem, dobrodružnou příhodou v délce denního hlášení, fyzikálním pozorováním, …).

Má-li z krystalu vycházet laserový paprsek, musíme mu dodat energii prostřednictvím záření z vnějšího zdroje. Cílem je, aby co nejvíce záření z našeho bodového zdroje bylo využito k excitaci elektronů ve velmi malém krystalu. Poraďte nám, jaký ideální tvar proto musí mít odrazná plocha. Nezapomeňte své tvrzení dostatečně zdůvodnit.

Tzv. Global Positioning System (GPS) pracuje na jednoduchém principu. Družice pohybující se na 12hodinových drahách vysílají přesně synchronizovaně signály, které příjmač detekuje. Protože na příjmači nejsou absolutně přesné hodiny, dokáže měřit jen rozdíly vzdáleností od různých satelitů. 4 satelity stačí na dopočtení polohy, poloha satelitů se změří ze Země stejným způsobem.

Zdůvodněte, proč je přesnost GPS v horizontálním směru znatelně vyšší než ve vertikálním směru.