Vyhledávání úloh podle oboru
Databáze úloh FYKOSu odjakživa
astrofyzika (85)biofyzika (18)chemie (24)elektrické pole (71)elektrický proud (76)gravitační pole (81)hydromechanika (146)jaderná fyzika (44)kmitání (57)kvantová fyzika (31)magnetické pole (43)matematika (89)mechanika hmotného bodu (298)mechanika plynů (87)mechanika tuhého tělesa (221)molekulová fyzika (72)geometrická optika (78)vlnová optika (65)ostatní (167)relativistická fyzika (37)statistická fyzika (21)termodynamika (155)vlnění (51)
mechanika tuhého tělesa
6. Série 11. Ročníku - 3. kostka
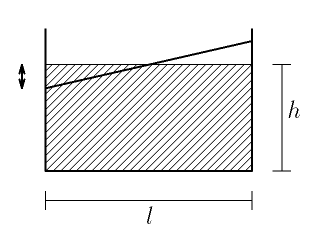
Když se pokusíme uchopit kostku tak, jak je naznačeno na obrázku, ne vždy se nám to povede. Určete podmínku, za které se to podaří.
6. Série 11. Ročníku - P. zastavení v zatáčce
Představte si, že jednou budou u nás vlaky jezdit opravdu rychle. Nechť rychlík zastaví v oblouku o poloměru $500\,\jd{ m}$, který je klopen pro rychlost $200\,\jd {km/h}$ (tzn. že na cestující v jedoucím rychlíku působí neustále síla jen kolmo dolů). A protože lidé jsou zvědaví, vykloní se všichni z oken na vnitřní straně oblouku, aby zjistili, co se děje. Vaším úkolem je zjistit, kolik lidí musí ve vlaku být, aby se překlopil.
Vlak je složen z 10 čtyřosých rychlíkových vozů o délce $25\,\jd{ m}$, šířce $3\,\jd{ m}$, výšce $4,2\,\jd{ m}$ a hmotnosti $40\,\jd{ t}$. Těžiště vozu je ve výšce $1,2\,\jd{ m }$ od hlavy kolejnice, rozchod koleji je $1738\,\jd{ mm}$. Spodní okraj otevřeného okna nechť je ve výšce $2,5\,\jd{ m}$.
5. Série 11. Ročníku - 4. cvičená opice
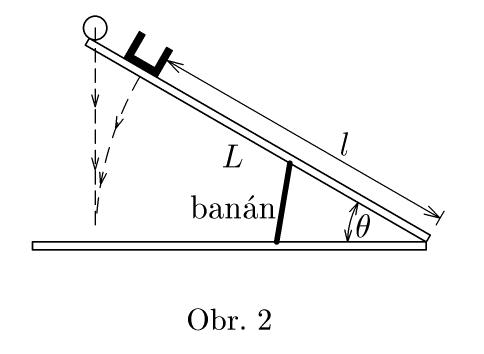
Konstrukce atrakce
Novopečený majitel zoologické zahrady by měl rád v pavilonu opic následující atrakci. Na jednom ze dvou prkýnek spojených pantem je ve vzdálenosti $l$ od pantu připevněn miniaturní košíček a na konci prkýnka (ve vzdálenosti $L$ od pantu) je položen míček. Prkýnko je podepřeno banánem, a svírá se zemí úhel $θ$. K této „aparatuře“ přijde hloupá opice (zatím nebyl čas ji vycvičit), a vezme si banán.
Vyvrcholením atrakce by mělo být to, že odbrzděné prkénko se dá do pohybu a míček by měl sám spadnout do košíčku. Diskutujte, zda-li je to vůbec možné a pokud ano, spočtěte jaké musí být $l$ v závislosti na $L$ a úhlu $θ$.
5. Série 11. Ročníku - P. samopal
Rozhodněte jak těžkou krychli lze převrátit střelbou ze samopalu (či spíše menšího děla) o parametrech 50 střel za sekundu, rychlost střely $500\, \jd{m. s^{-1}}$, hmotnost střely $100\,\jd{ g}$. Krychle má hranu dlouhou $1\,\jd{m}$, po podložce neklouže.
4. Série 11. Ročníku - 1. soutěž jehlanů
Vezmeme dva jehlany stejných rozměrů se čtvercovou podstavou o délce podstavné hrany $a$ a výšce $v$. Kromě toho, že jejich rozměry jsou stejné, i jejich hmotnost je stejná. Jeden má drátěné hrany a druhý má plechové stěny. Postavíme je vedle sebe na podložku, kterou začneme naklánět. Který z modelů se dříve překlopí? Tření je tak velké, že jehlany po podložce nebudou klouzat.
3. Série 11. Ročníku - 1. jeřáb
Jeřáb může zdvihat břemeno pouze konstantní svislou silou $F$. Budeme jím zvedat ze země nekonečné lano o délkové hustotě $µ$. Jakou maximální rychlost jeho horní konec během pohybu dosáhne? Jakou maximální výšku dosáhne?
3. Série 11. Ročníku - 4. válec versus kvádr
Mějme homogenní válec a homogenní kvádr. Obě tělesa jsou vyrobena ze stejného materiálu a mají stejnou hmotnost. Hodíme je současně vedle sebe na stůl stejnou počáteční rychlostí $v_{0}$ (hodíme je rovnoběžně s rovinou stolu, svislá složka rychlosti při dopadu je nulová). Válec se na počátku neotáčí. Rozhodněte, které těleso se bude pohybovat rychleji, případně diskutujte fáze pohybu, kdyby se jejich vzájemná pozice s časem měnila. Uvažujte pohled jak silový, tak energetický. Uvažujte, že smyková třecí síla je charakterizovaná pouze součinitelem smykového tření, tj. základní model, kdy smyková třecí síla závisí pouze na normálové přítlačné síle. Valivé tření neuvažujte.
3. Série 11. Ročníku - E. fyzik hudebníkem
Změřte součinitel klidového tření mezi různými materiály (např. papír a dřevo). Při měření využijte gramofonu.
2. Série 11. Ročníku - 2. odraz
Gumová kulička o průměru $1\,\jd{ cm}$ dopadá na ocelovou desku z výšky dvou metrů. Odhadněte řádově, jak velké bude její průměrné zrychlení během odrazu.
1. Série 11. Ročníku - 2. zlaté sloupy
Dva identické zlaté sloupy výšky $200 \,\jd{m}$ a průřezu $1 \,\jd{dm^2}$ jsou umístěny vedle sebe. Jeden z nich je zavěšený a druhý stojí na podložce, oba mají stejnou teplotu $0 \,\C$. Oběma dodáme teplo $5\cdot 10^{6}\, \jd{kJ}$. Budou mít potom stejnou teplotu? Jestliže ne, odhadněte, o kolik se jejich teplota bude lišit. Potřebné údaje si najděte v tabulkách, tepelnou výměnu s okolím zanedbejte.