Vyhledávání úloh podle oboru
Databáze úloh FYKOSu odjakživa
astrofyzika (85)biofyzika (18)chemie (24)elektrické pole (71)elektrický proud (76)gravitační pole (81)hydromechanika (146)jaderná fyzika (44)kmitání (57)kvantová fyzika (31)magnetické pole (43)matematika (89)mechanika hmotného bodu (298)mechanika plynů (87)mechanika tuhého tělesa (221)molekulová fyzika (72)geometrická optika (78)vlnová optika (65)ostatní (167)relativistická fyzika (37)statistická fyzika (21)termodynamika (155)vlnění (51)
elektrický proud
(2 body)3. Série 29. Ročníku - 2. alchymista začátečník
Náš nejmenovaný mladý alchymista, říkejme mu Jirka N., se naučil používat elektrolýzu a měřit elektrochemický ekvivalent látky. Dokonce se mu podařilo naměřit u jednoho vzorku hodnotu elektrochemického ekvivalentu relativně přesně, a to $A=(6,\! 74 ± 0,\! 01) \cdot 10^{-7}\;\mathrm{kg}\cdot \mathrm{C}^{-1}$. Ale sám si neví rady, jak určit, o jakou látku se jedná. Poraďte mu!
Karel učil elektrolýzu.
(2 body)1. Série 29. Ročníku - 1. zahušťující Hofmann
Při elektrolýze vody v Hofmannově přístroji je elektrolytem roztok kyseliny sírové ve vodě. Hmotnost kyseliny v roztoku je prakticky konstantní, ale jak již samotný název napovídá, voda se postupně rozkládá na vodík a kyslík. Tím se zvyšuje zastoupení kyseliny v roztoku. Za jak dlouho stoupne hmotnostní zlomek kyseliny v roztoku na dvojnásobek, pokud roztokem prochází proud $I=1\; \textrm{A}$, původní hmotnostní procento kyseliny bylo $w_{0}=5\; \%$ a objem roztoku v nádobě byl původně $V_{0}=2\; \textrm{l}$?
Karel opět přemýšlel nad elektrolýzou.
(2 body)4. Série 28. Ročníku - 1. čtvercatý odpor
Jak závisí elektrický odpor čtverce na délce jeho strany $a?$ Všechny čtverce, o které se zajímáme, jsou samozřejmě vodiče vyrobené z tenkého materiálu o tloušťce $h$ a měrném elektrickém odporu $ρ$. Zajímáme se o odpor mezi protilehlými stranami čtverce.
Karel se inspiroval na Veletrhu nápadů učitelů fyziky 19.
(8 bodů)1. Série 28. Ročníku - E. nabitá brambora
Změřte zátěžovou charakteristiku brambory jako zdroje elektrického napětí se zapojenými elektrodami z různých kovů.
Karel přemýšlel nad jednoduchými pokusy.
(4 body)5. Série 27. Ročníku - 4. trojúhelníkový odporníček
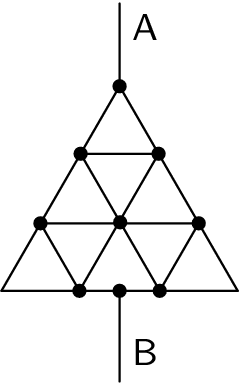
Určete odpor trojúhelníku vytvořeného z odporového drátu mezi svorkami A a B, které vidíte na obrázku. Jedna strana malého trojúhelníčku (ze kterých se skládá velký trojúhelník) má odpor $R_{0}$. Odpor přívodních vodičů neuvažujte.
Karel si maloval trojúhelníčky.
(4 body)2. Série 27. Ročníku - P. Temelínská
Odhadněte, kolik jaderného paliva se spotřebuje v jaderné elektrárně na $1\;\jd{MWh}$ elektrické energie, kterou spotřebují lidé až v domácnosti. Srovnejte to se spotřebou paliva v tepelné elektrárně. Nezapomeňte uvažovat všechny možné ztráty.
Bonus: Uvažte i energii, která se spotřebuje při těžbě a přepravě potřebných surovin.
Karel přemýšlel nad ČEZem.
(4 body)1. Série 26. Ročníku - 3. Poledniková
Nechť jsou podél poledníků a rovnoběžek natažené dráty, které jsou v místech křížení spojené. Jaký naměříme odpor mezi body sítě, které odpovídají zemským pólům, pokud víte, že odpor jednoho metru drátu je $ρ$. Poledníky i rovnoběžky uvažujte po 15$°$.
Bonus: Jaký je odpor mezi dvěma uzly sítě, které leží na rovníku a naproti sobě?
Honza Hum. honil Janapku po poledníku.
4. Série 23. Ročníku - P. úleva u ohradníku
Zamyslete se nad tím, jak je to s odporem tekoucího elektrolytu. Je jeho velikost závislá na tom, jestli teče po směru elektrického proudu v něm, nebo naopak? Zkuste odhadnout rozdíl, je-li.
ránu dostal Grepe
6. Série 22. Ročníku - 1. odpor je marný
Vypočítejte odpor $n$-rozměrné krychle mezi dvěma nejvzdálenějšími vrcholy (ty o souřadnicích $(0$, $0$, …, $0)$ a $(1$, $1$, …, $1)$. Zkuste začít od trojrozměrné a použijte stejný postup.
Přednesl Lukáš Ledvina
4. Série 22. Ročníku - P. zachraňte fyziku
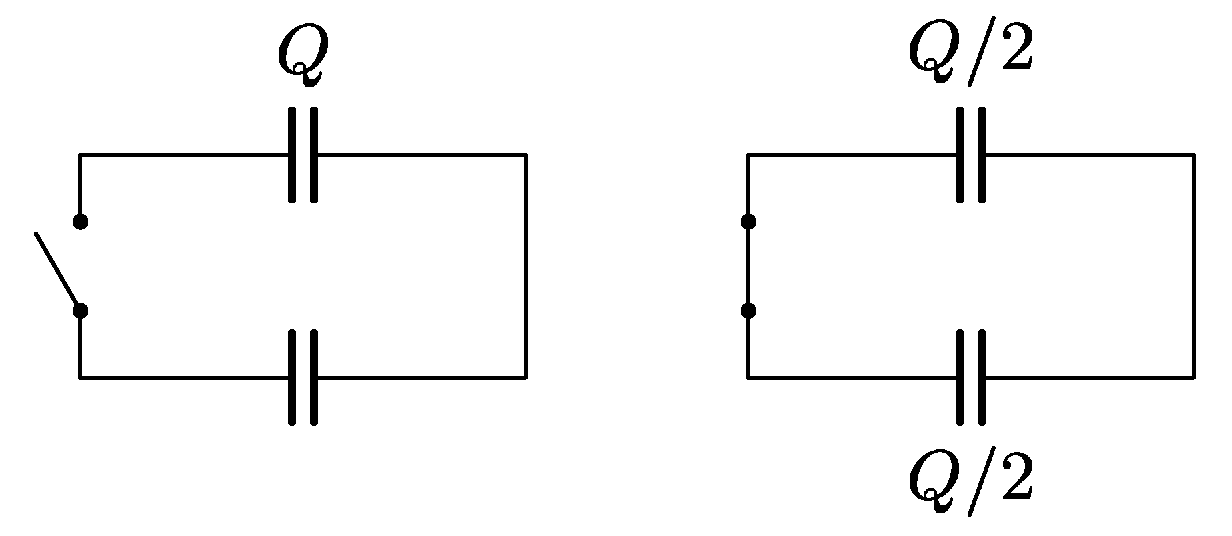
Rozpojený obvod na obrázku obsahuje jeden nenabitý a jeden nabitý kondenzátor (náboj $Q)$. Vodiče jsou ideální, nemají žádný odpor, oba kondenzátory jsou stejné. Celková energie nábojů v obvodu tedy je $Q⁄2C$. Pokud se po sepnutí vypínače náboje na kondenzátorech vyrovnají, celková energie bude $Q⁄8C+Q⁄8C=Q⁄4C$, což je polovina oproti počáteční situaci. Vysvětlete tento rozdíl. Kde se spotřebovala polovina energie? Vypínač je vyrobený tak šikovně, že v něm vysvětlení netkví.
S touhle záludností přišel Jarda Trnka.