Vyhledávání úloh podle oboru

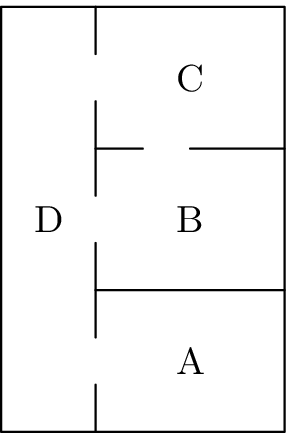
Aleš bydlí ve čtyřpokojovém bytě, jehož půdorys si můžete prohlédnout na obrázku. Mára se ale rozhodl, že Alešův byt zamoří nepříjemnými mravenci faraony. Faraoni po bytu šíleně rychle pobíhají a to ještě navíc šíleným způsobem – můžete uvažovat, že jednou za pět minut se 60$%$ mravenců přesune do sousedních místností a jenom 40$%$ jich zůstává pobíhat ve stejné místnosti, co předtím. Přitom se rovnoměrně rozbíhají do sousedních místností (když má místnost dvoje dveře, tak 30$%$ jich přeběhne do jedné a 30$%$ do druhé, když má troje dveře, tak se rozdělí po 20$%)$. A to se opakuje každých pět minut (uvažujte jenom kroky přesně po pěti minutách). Faraonům se v bytě líbí a tak neutíkají ven. Na druhou stranu se faraoni nemají šanci jinak dostat do bytu než propašováním a to dělá jenom Mára, takže jinak ani faraoni v bytu nepřibývají.

• Když Mára zlomyslně umístí 1000 faraonů do předsíně (D), kolik faraonů bude v jednotlivých místnostech po pěti minutách? Kolik jich bude po deseti minutách a po patnácti minutách? (2 body)

• Pokud jsme našli v místnostech počty mravenců $N_{A}=12$, $N_{B}=25$, $N_{C}=25$ a $N_{D}=37$, jak byli mravenci rozmístění před pěti minutami? (1 bod)

• Bonus: Kolik mravenců by bylo v místnostech po hodně dlouhé (prakticky nekonečné) době, když by Mára rozmístil faraony jako v bodu a)? Závisí to na tom, jak Mára mravence rozmístil? A nejrafinovanější otázka - ustálí se počet mravenců na jedné hodnotě, nebo bude oscilovat? (bod/y navíc)

Maminka má kočárek o hmotnosti $m$ a je s ním pevně spojena vláknem délky $l$, které je na počátku natažené. Mezi maminkou i kočárkem a podlahou, na které oba stojí, je nenulový koeficient smykového tření $f$. Maminka začne kočárek táhnout po přímce konstantní rychlostí $v$, která je kolmá na počáteční polohu vlákna. Popište trajektorii kočárku v závislosti na parametrech úlohy. Maminku i kočárek považujte za hmotné body. Doporučujeme úlohu numericky simulovat.

Hodíme kulatý kámen o hmotnosti $m$ z výšky $h$ nad hladinou do rybníka o hloubce $d$. Přibližně za jak dlouho spadne na dno? Jak se výsledek změní, když kámen nebude kulatý, ale placatý?

Model rakety má motůrek, jenž dává konstantní tah, dokud má palivo o počáteční hmotnosti $m_{p}$. Prázdná raketa váží $m_{0}$ a motor palivo spaluje lineárně s časem. Do jaké výšky může raketa vyletět, letí-li v homogenním gravitačním poli a zanedbáme-li odpor vzduchu?

Pepička si koupila žárovičku, dva přepínače a klubko drátu. Jak má žárovičku a přepínače zapojit, aby změnou polohy kteréhokoli přepínače žárovička vždy změnila stav mezi svítí/nesvítí? Jak by to bylo, kdyby chtěla Pepička takto zapojit víc než dva přepínače?

Plavec se snaží přeplavat řeku, v níž teče voda rychlostí $v_{r}=2\;\mathrm{km/h}$. Sám přitom plave rychlostí $1\;\mathrm{m/s}$. Po jaké dráze a jakým směrem musí plavat, aby se nejméně namohl? V jakém místě a za jak dlouho vyplave na druhý břeh? A co aby jeho dráha byla nejkratší? Šířka řeky je $d=10\;\mathrm{m}$.

• Popište geometrickou konstrukci (pomocí kružítka a pravítka) profilu Žukovského.
• Zkuste nakreslit proudnice v okolí profilu Žukovského. Zvolte si takové parametry $d/l$ a $m/l$, aby měly praktické opodstatnění.
• Jaká vztlaková síla působí na rovnou desku? Jaká vztlaková síla působí na desku tvaru kruhového oblouku?
• Zkuste nakreslit profil křídla odpovídající Karmánově-Trefftzově transformaci.

• Dokažte tvrzení d), podle něhož Möbiova transformace zachovává úhly. Jedna z možností je uvědomit si, že v kruhové inverzi existují kružnice, které se zobrazují samy na sebe.
• Najděte podmínku na koeficienty Möbiovy transformace, aby zobrazovala komplexní kruh na komplexní kruh (|$z|$ = 1) a najděte konkrétní transformaci, která zobrazuje komplexní kruh na horní komplexní polorovinu. Co to fyzikálně znamená?
• Podle teorie relativity se tělesa pohybující se rychlostí blízkou rychlosti světla zkracují (Lorentzova kontrakce). To ovšem ještě neznamená, že bychom je viděli kratší (například, že bychom místo pohybující se koule viděli pohybující se elipsoid). Využijte představy, který jsme v tomto díle vybudovali, abyste odvodili, že předměty letící rychlostí světla vidíme o kousek pootočené, nikoliv zkrácené (Terellova rotace).

a) Uvědomte si, že $n$-té odmocniny z komplexní jednotky leží na $n$-úhelníku, a dořešte Bombelliho rovnici $x^{3}-15x-4 = 0$. Nápovědu naleznete v textu seriálu.

b) Vyjádřete goniometrické součtové vzorce pomocí komplexních exponenciál.

c) Ukažte oprávněnost zanedbání vyšších mocnin v odvození Bernoulliho limity, tj. že do závorky můžeme přidat člen $o(1/N)$.

d) Použijte značení s malým $o$, abyste vyřešili úlohu, s jakou frekvencí kmitají body hmotnosti $m$ po ose $x$ v Yukawově potenciálu $\frac{k}{x}e^{x/λ}$ kolem rovnovážné polohy.

e) Dokažte, že Čebyševovy polynomy $\cos(n \arccos x)$ jsou skutečně polynomy.

Návod: Uvažujte komplexní jednotku $z$, která má reálnou část $x$. Pak se vyšetřovaný výraz rovná reálné části $z^n$, což musí být polynom, protože odmocniny a imaginární jednotky drží pospolu.

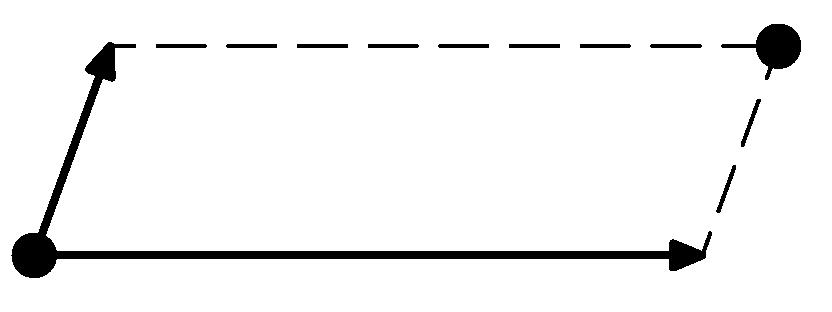
Pomocí dvou různých vektorů v rovině můžeme opakovaným posouváním počátečního bodu dostat nekonečnou mříž bodů (viz obrázek). (Stejným způsobem vznikne krystal, jen místo bodu posouváme skupinu atomů.) Posunutím celé mříže o jeden z vektorů dostaneme stejnou mříž, tj. každý bod bude nahrazen jiným bodem. Stejně tak se může stát, že otočením celé mříže kolem jednoho bodu o nějaký úhel dostaneme stejnou mříž. Najděte všechny úhly, pro které je to možné, a nakreslete, jak vypadají mřížky s touto rotační symetrií.