Vyhledávání úloh podle oboru
Databáze úloh FYKOSu odjakživa
astrofyzika (85)biofyzika (18)chemie (24)elektrické pole (71)elektrický proud (76)gravitační pole (81)hydromechanika (146)jaderná fyzika (44)kmitání (57)kvantová fyzika (31)magnetické pole (43)matematika (89)mechanika hmotného bodu (298)mechanika plynů (87)mechanika tuhého tělesa (221)molekulová fyzika (72)geometrická optika (78)vlnová optika (65)ostatní (167)relativistická fyzika (37)statistická fyzika (21)termodynamika (155)vlnění (51)
elektrický proud
(12 bodů)3. Série 32. Ročníku - E. indexovaný kondenzátor
Poštou vám přišel elektrolytický kondenzátor a rezistor. Změřte kapacitu kondenzátoru a odpor rezistoru, neměřte je však přímo. Součin kapacity kondenzátoru a odporu rezistoru je přibližně $RC\approx 20 \mathrm{s}$.
Varování Elektrolytický kondenzátor má kladnou a zápornou elektrodu, při zapojení opačně ho můžete zničit. Maximální dovolené napětí je $10 \mathrm{V}$.
Dodo právě v praktitku měřil rezonanci.
(10 bodů)3. Série 32. Ročníku - P. osobní powerbanka
Poslední procenta baterky v mobilu dochází, powerbanku máte vybitou nebo jste si ji pro jistotu nechali doma a 230 také není nikde v dohledu. Nebylo by skvělé mít neustále při sobě vlastní zdroj elektrické energie?
- Navrhněte několik různých zařízení, která by dokázala vyrábět elektrickou energii pouze ze zdrojů vašeho těla.
- Diskutujte jejich maximální výkon a účinnost. Co všechno byste s jejich pomocí dokázali zásobovat elektřinou?
- Diskutujte jejich dopad na vaše zdraví a fyzickou kondici. Které orgány by vám v důsledku jejich přetěžování selhaly nejdříve?
Jako jedno z možných zařízení uvažujte soustavu drobných turbín umístěných v krevním řečišti. Všechny argumenty podpořte co nejpřesnějšími výpočty.
Jáchym měl pocit, že mu chybí nějaká energie.
(8 bodů)1. Série 32. Ročníku - 5. zpropadený obvod
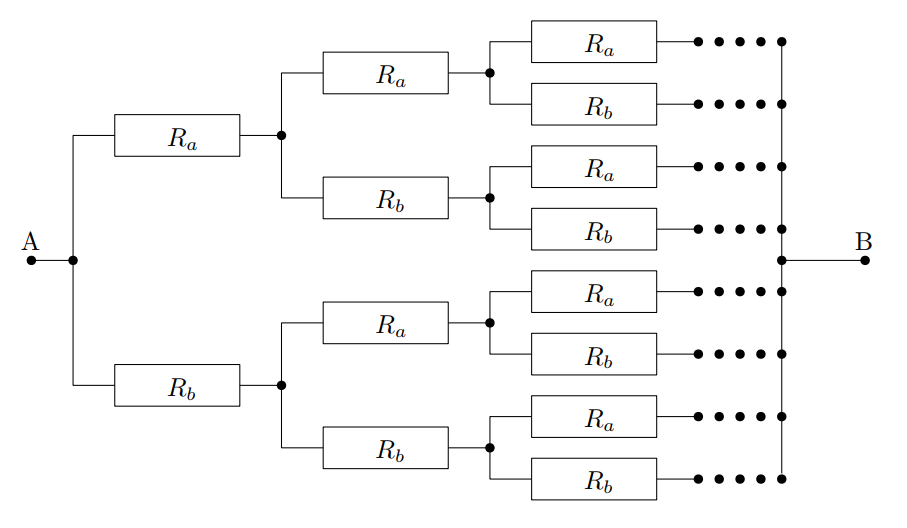
a) Určete odpor nekonečné odporové sítě na obrázku mezi body A a B. Bod A je přímo spojen s dvěma rezistory s odpory $R_a$ a $R_b$. Každý z těchto rezistorů je spojen s dalšími dvěma odpory $R_a$ a $R_b$ a tak dále.
b) Na obrázku si místo rezistorů představte kondenzátory s kapacitami $C_a$ a $C_b$. Jaká bude celková kapacita obvodu?
Karel zase jednou chtěl něco nekonečně-nekonečného.
(3 body)6. Série 31. Ročníku - 2. horký drát
Vypočítejte proud, který by měl procházet kovovým vláknem s průměrem $d = 0{,}10 \mathrm{mm}$ nacházejícím se ve vakuové baňce, aby teplota vlákna měla stálou hodnotu $T = 2 600 K$. Předpokládejte, že povrch vlákna září jako ideální černé těleso. Zanedbejte ztráty tepla způsobené vedením tepla. Rezistivita materiálu vlákna při dané teplotě je $\rho = 2{,}5 \cdot 10^{-4} \mathrm{\Omega \cdot cm}$.
Nápověda. Použijte Stefanův-Boltzmannův zákon.
Danka rozmýšľala nad efektivitou žiaroviek.
(7 bodů)4. Série 31. Ročníku - 4. vymyslete si sami
Máme černou skříňku se třemi výstupy (A, B a C). Víme, že obsahuje $n$ rezistorů se stejným odporem, ale nevíme jak jsou zapojeny. Změříme tedy odpory mezi dvojicemi bodů AB, BC a CA a zjistíme, že $R\_{AB} = 3 \mathrm{\Omega }$, $R\_{BC} = 5 \mathrm{\Omega }$ a $R\_{CA} = 6 \mathrm{\Omega }$. Zjistěte, kolik nejméně rezistorů může skříňka obsahovat a určete příslušný odpor jednoho rezistoru.
Matěj to vymyslel velmi rychle.
(6 bodů)0. Série 31. Ročníku - 3. (ne)odporný drát
Uvažujte kruhový drát s nulovým odporem a délkou $l$, který se nachází v magnetickém poli s magnetickou indukcí kolmou na rovinu drátu, pro jejíž velikost v čase platí $B = kt$, kde $k$ je nějaká konstanta. Na drátu označíme dva body $A$ a $B$, čímž jej rozdělíme na dvě části, jednu se čtvrtinou původní délky a druhou se třemi čtvrtinami původní délky. Jaké napětí naměříme mezi body $A$ a $B$?
(3 body)2. Série 30. Ročníku - 2. hypervysokoteplotní supravodivost
Velké části látek, obvykle kovům, roste s vyšší teplotou odpor. Jsou ovšem látky, jako například grafit či polovodiče, kterým odpor s rostoucí teplotou klesá. Také jste již pravděpodobně slyšeli o supravodivosti, což je jev, který obvykle nastává za velmi nízkých teplot a jedná se o stav, ve kterém látka nevykazuje žádný elektrický odpor a dokonale vede elektrický proud. V současné době jsou nejvyšší teploty, ze kterých byla supravodivost pozorována, hluboko pod pokojovou teplotou. Co kdybychom ale uvažovali, že se odpor mění dle vzorečku $R=R_{0}(1+αΔt)$, kde $R_{0}$ je odpor vodiče pro $20\; \mathrm{°C}$, $α$ je teplotní součinitel elektrického odporu a $Δt$ teplotní rozdíl vůči původní teplotě $20\; \mathrm{°C}$? Tak při hodnotách součinitelů pro grafit $α_\mathrm{C}=-0,\! 5 \cdot 10^{-3}\; \mathrm{K^{-1}}$ a křemík $α_\mathrm{Si}=-75 \cdot 10^{-3}\; \mathrm{K^{-1}}$ dostáváme nulový odpor pro vysoké teploty. Pro jaké? A jak to, že to ve skutečnosti nefunguje a jak uhlík, tak křemík nejsou za vysokých teplot supravodivé?
Karel se inspiroval nekonstantními konstantami.
(4 body)6. Série 29. Ročníku - 4. fire in the hole
Pro ohřev plasmatu ve fúzních zařízeních se používají svazky neutrálních částic. V takovém zařízení se nejprve urychlí ionty deuteria na vysokou energii a následně se přenosem náboje neutralizují, přičemž si zachovávají téměř původní rychlost. Na tokamaku COMPASS mají částice na výstupu ze svazku energii $40\; \mathrm{keV}$ a proud ve svazku těsně před neutralizací je $12\; \mathrm{A}$. Jaká síla působí na generátor svazku? Jaký je jeho výkon?
Aleš koukal na vypálenou díru ve ventilu.
(2 body)5. Série 29. Ročníku - 1. už to teče
Tenký drát s odporem $R=100\;\mathrm{mΩ}$ a délkou $l=1\;\mathrm{m}$, který je připojen ke zdroji stejnosměrného napětí $U=3\;\mathrm{V}$, obsahuje ve svém objemu $N=10^{22}$ volných elektronů, kterými přispívá k toku elektrického proudu. Určete, jak velkou průměrnou (přesněji střední) rychlostí se elektrony v drátu pohybují.
Mirek už zase slyšel, že částice ve vodiči tečou rychlostí světla.
(7 bodů)5. Série 29. Ročníku - E. fotografická
Pomocí digitálního fotoaparátu změřte frekvenci střídavého proudu v síti. Postačí i chytrý telefon s vhodnou aplikací, která umožní nastavit přesnou hodnotu expozičního času.
Populární přednášky z fyziky na střední.