Vyhledávání úloh podle oboru

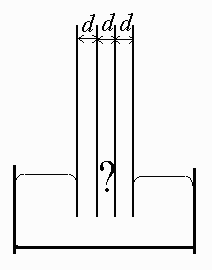
Mějme dvě tenounké trubičky, jednu o průměru $d$, druhou o průměru $3d$, přičemž menší z nich je souose vsunuta do větší (opačně by to nejspíše nešlo). Tuto soustavu ponoříme jedním koncem do misky se rtutí, jak je to vidět na obrázku. V jaké výšce se ustálí hladina rtuti uvnitř tenčí kapiláry a v mezeře mezi oběma kapilárami vzhledem k hladině v misce?

Může bitevní loď plovat ve vaně?

Máme samozřejmě na mysli dostatečně malou loď nebo dostatečně velkou vanu. V každém případě je okolo lodě málo vody v porovnání s jejím objemem (viz obr. 1). Mějme konkrétně loď o hmotnosti $100\;\textrm{tun}$ a vanu, ve které je $1\;\textrm{m}^{3}$ vody.

Pokuste se experimentálně určit hustotu vzduchu, pokud máte k dispozici dva různě velké balónky napuštěné plynem lehčím než vzduch. (Nevíme, jak je to s pouťovým šílením v této době jestliže neseženete vhodný plyn, např. vodík, zkuste použít horký vzduch – chyba měření bude ovšem ďábelská. Případně můžete měřit s plynem těžším vzduchu).

Nápověda: Neznámé hustoty náplně balónku se při výpočtu zbavíte právě tím, že provedete měření pro dva různé balónky, čili ze dvou rovnic tuto neznámou vyloučíte.

V uzavřeném skleněném zvonu je hladina rtuti a na ní plave ocelová kulička. Rozhodněte, jak se kulička pohne, pokud vyčerpáme ze zvonu vzduch.

Položíte-li na nakloněnou rovinu dvě láhve, jednu prázdnou a jednu plnou, která z nich se bude kutálet rychleji (jsou to téměř válcové nádoby, osa symetrie kolmo na spádnici)? Pohyb na nakloněné rovině uvažujte bez tření a podkluzování. Přechází-li rovina v hrubší vodorovnou plochu, která z nádob po ní dojede dál? A uvedeme-li je na úpatí nakloněné roviny prudce do pohybu směrem vzhůru, která vyjede výše?

V koupelně je kohout na teplou a studenou vodu, již lze pouštět jak do vany, tak do sprchy. Pustíme-li naplno studenou vodu, trvá napouštění vany přímo $t_{1}\;\mathrm{minut}$, přes sprchu $t_{2}\;\mathrm{minut}$. Pokud otevřeme jen kohout teplé vody, prodlouží se napouštění vany na $t_{3}\;\mathrm{minut}$ přímo a $t_{4}$ přes sprchu. Určete, jak dlouho trvá napouštění (přímo i přes sprchu), otevřeme-li oba kohouty (případně počítejte s tím, že studená voda má teplotu $T_{1}$ a teplá teplotu $T_{2})$.

Velké množství dutých válců se zmenšujícími se průřezy je vnořeno do sebe a zalito vodou tak, že válec s menší plochou dna vždy plave ve válci, do kterého je vsazen (viz obr. 1). Nejmenší válec má plochu dna rovnu $S_{0}$, a ta je mnohem menší než plocha dna vnějšího válce. Vzdálenosti mezi dny jednotlivých válců jsou dostatečně velké, aby nikdy nedošlo k dotyku. Do nejmenšího válce přilijeme objem vody $V_{0}$. Po dolití opět válce v sobě plovou. O jakou vzdálenost a jakým směrem se posune dno nejmenšího válce vzhledem k nehybné podložce?

Může bitevní loď plavat ve vaně? Máme samozřejmě na mysli dostatečně velkou vanu nebo dostatečně malou loď. V každém případě je okolo lodě celkem málo vody. Mějme konkrétně loď s hmotností $100\; \textrm{tun}$ a vanu, ve které je $1\; \textrm{m}$ vody.

Mějme tři bazény. V každém z nich plave kus ledu tak, jak ukazují obrázky. Hladina vody sahá vždy přesně po okraj bazénu. Led v bazénu na obr. 1 obsahuje vzduchovou bublinu. V bazénu 2 plave led s dutinou vyplněnou nezmrzlou vodou. Led v bazénu 3 obsahuje kousek železa. Určete, ve kterých bazénech voda po roztání ledu:

• přeteče
• poklesne
• zůstane těsně po okraj

Pohybuje-li se těleso v kapalném nebo plynném prostředí, působí na něj prostředí odporující silou, závislou na rychlosti tělesa. Navrhněte nějakou jednoduchou metodu (realizovatelnou doma, ve škole atp.), kterou by bylo možno alespoň přibližně určit závislost rychlosti tělesa pohybujícího se ve vzduchu. Navržené experimenty proveďte a zhodnoťte výsledky.

Návod: Předpokládejte závislost tvaru $F = av^{b}$.