Vyhledávání úloh podle oboru
Databáze úloh FYKOSu odjakživa
astrofyzika (85)biofyzika (18)chemie (24)elektrické pole (71)elektrický proud (76)gravitační pole (81)hydromechanika (146)jaderná fyzika (44)kmitání (57)kvantová fyzika (31)magnetické pole (43)matematika (89)mechanika hmotného bodu (298)mechanika plynů (87)mechanika tuhého tělesa (221)molekulová fyzika (72)geometrická optika (78)vlnová optika (65)ostatní (167)relativistická fyzika (37)statistická fyzika (21)termodynamika (155)vlnění (51)
kmitání
5. Série 9. Ročníku - P. rotující kyvadýlka
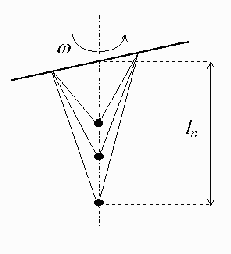
Představte si, že máte na tyčce připevněno pomocí dvou závěsů několik kuliček tak, že se mohou pohybovat po kružnici o poloměru $l_{n}$ (ve svislé rovině), kde $n$ je pořadové číslo kuličky. Potom celou soustavu roztočíme podél svislé osy úhlovou rychlostí $ω$ a nepatrně do kuliček šťouchneme (aby nebyly přímo na ose rotace). Co se děje s jednotlivými kuličkami a jak bude vypadat pohled z boku na tuto rotující soustavu?
5. Série 8. Ročníku - P. co ten skokan pořád chce
Chceme-li demonstrovat metodu řešení soustavy rovnic na našem skokanovi, budeme muset přidat další podmínku: dejme tomu, že první dopad na prkno se mu zdál příliš tvrdý; rozhodl se tedy rozkývat prkno natolik (změnit amplitudu kmitů), aby druhá srážka s prknem proběhla se zanedbatelnou vzájemnou rychlostí. Tedy jak hodnota Funkce, tak Derivace (uvedená v minulém díle) byla v okamžik srážky rovna nule. Vašim úkolem je najít potřebnou amplitudu $A_{n}$ a dobu druhého skoku $T_{n}$ (odráží se opět dole).
2. Série 8. Ročníku - P. problém liftboye
Liftboy v mrakodrapu si pověsil na stěnu svého výtahu přesné kyvadlové hodiny, aby viděl, kdy mu končí pracovní doba. Doba pohybu výtahu se zrychlením vzhůru a dolů je stejná. Zrychlení taktéž. Co si myslíte: bude mít chlapec pracovní dobu delší, kratší nebo stejnou?
2. Série 8. Ročníku - S. skokan
Skokan na můstku se odrazí z prkna rychlostí $v=5\;\mathrm{m}\cdot \mathrm{s}^{-1}$ kolmo vzhůru v okamžiku, kdy je deska maximálně prohnutá směrem dolů (o $A=30\;\mathrm{cm}$ pod rovnovážnou polohou). Za jak dlouho se opět s deskou srazí, pokud prkno kmitá s periodou $T=0,5\;\mathrm{s}$.
Srovnejte rychlost výpočtu v jednotlivých fázích (hrubé přibližování, dolaďování).
1. Série 7. Ročníku - 2. gramofonová přenoska
Raménko s gramofonovou přenoskou je uchyceno v čepu a vyváženo závažím. Pokuste se zdůvodnit proč je celá soustava uspořádána tímto způsobem. Navrhněte velikost a umístění závaží, je-li hmotnost přenosky 15 g, tuhost jehly ve vertikálním směru 80 N\cdot m^{−1} a její vzdálenost od čepu je asi 200 mm, víte-li, že maximální přípustná síla, jíž může jehla tlačit na desku je 0,02 N. Hmotnost ramena přenosky zanedbejte.
1. Série 7. Ročníku - P. fošna
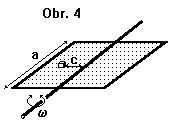
Čtvercová deska o straně délky $a$ (viz obr. 4) je upevněna na ose procházející jejím středem ve směru rovnoběžném s jednou ze stran. Ve vzdálenosti $c$ od této osy je na ní položeno malé tělísko hmotnosti $m$. Deska začne kmitat s nevelkou amplitudou kolem vodorovné polohy s frekvencí $ω$. Určete dobu (je mnohem větší než perioda kmitů), za kterou tělísko spadne z desky, je-li koeficient tření mezi deskou a tělískem $μ$.
3. Série 1. Ročníku - 3. tramvaj
Ve stojící tramvaji visí u svislé desky na niti délky $l$ citrón o hmotnosti $m$ (předpokládáme, že rozměry citrónu jsou velmi malé v porovnání s délkou niti). Tramvaj se rozjede se zrychlením $a$, které můžeme považovat za konstantní. Spočtěte, kam až toto kyvadlo vykývne (jaký maximální úhel bude svítat s deskou) a kdy citrón opět ťukne do desky.
2. Série 1. Ročníku - 4. pružiny
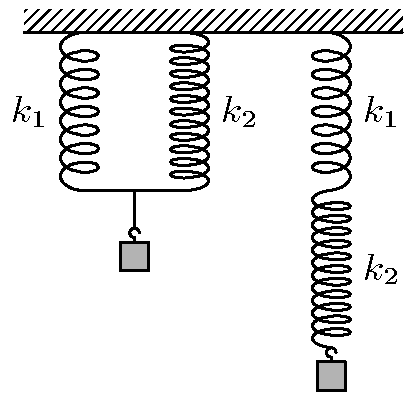
Model pružin
Pohrajme si s dvěma stejně dlouhými, ale různě tuhými pružinami. (Jejich tuhosti označíme $k_{1}$ a $k_{2}$.) Když je spojíme (viz obrázek), chovají se dohromady jako jediná pružina? Jaká je tuhost $k_{výsl}$ této „výsledné“ pružiny při spojení vedle sebe a jaká při spojení za sebou?
1. Série 1. Ročníku - 3. klavír
Předpokládejte, že vlastníte výborný koncertní klavír. Chcete ho nechat naladit. Pozvete nejlepšího ladiče pian. Ten ladí klavír tak, že porovnává zvuk klavíru a etalonu (ladičky). Jak dlouho mu bude trvat perfektní naladění klavíru?
- zhruba hodinu
- zhruba den
- zhruba týden
- zhruba měsíc
- nekonečně dlouho
1. Série 1. Ročníku - P. píst
V nádobě uzavřené pohyblivým pístem je ideální plyn. Píst stlačíme z jeho rovnovážné polohy o malou vzdálenost $x$ ($x$ je mnohem menší než výška nádoby $h)$ a pak jej pustíme. Následný děj považujeme za izotermický.
- Ukažte, že píst bude vykonávat harmonické kmity kolem rovnovážné polohy a najděte jejich frekvenci. (Návod: Uvažte síly působící na píst a jejich analogii se silami působícími na hmotný bod zavěšený na pružině.)
- Diskutujte oprávněnost předpokladu o izotermičnosti uvažovaného děje.