Vyhledávání úloh podle oboru

Kdesi v dalekém vesmíru za 1001 hvězdami a jednou černou dírou byla nebyla planeta Balónků. Tyto inteligentní duté bytosti každý rok pořádají soutěž „Čím výš, tím líp“.

Každý z balónků si přiváže provázek, aby bylo možné určit jeho výšku. Aby se mohli Balónci účastnit soutěže, musí mít všichni stejné parametry. Kupodivu nikdo zatím nikdy nevyhrál. Délková hustota provázku je 11 luftíků na špurgl, hustota atmosféry je 110101 luftíků na krychlový špurgl, poloměr každého z balónků je 10 špurglů, hmotnost Balónka je 10 luftíků. Při pádu tělesa v tíhovém poli na planetě Balónků se za každý temp jeho rychlost zvýší o 111 špurglů za temp. Určete, jakou maximální výšku Balónka hlavní rozhodčí soutěže naměří a jak se bude Balónek pohybovat po dosažení této výšky. Nezvednutá část provázku každého Balónka leží volně na zemi. Závody Balónků probíhají v malých výškách, kde je hustota atmosféry přibližně konstantní.

Nápověda: Každý balónek má maximálně jeden provázek.

V hlavním městě planety Balónků Medicinbaldorfu se jednou za debrecinský megatemp koná pouť. Hlavní atrakcí je speciální balónkovský kolotoč, který se Funík s Pískalem rozhodli navštívit.

Dutou tyčí délky $L$ je provlečen provázek délky $l>L$. Na jeden konec provázku se přivázal Funík, na druhý konec Pískal. Oba kamarádi by měli vážit stejně, Funík ale ke snídani snědl kousek rozemleté traverzy a je o trošku těžší. Poté se tyč začne točit kolem svislé osy na ní kolmé. Určete polohu osy tak, aby vodorovná vzdálenost mezi Balónky byla co největší.

… a už zní svatební síní slavnostní pískot a fukot. Ano, je to tak, Pískal s Foukalkou si dnes řeknou své písk. A už je tu první novomanželský polibek, při němž se spojí svými otvory. Poté kněz slavnostně rozváže provázky a dojde k propojení. Popište, co bude následovat. Nezapomeňte, že všichni svobodní Balónci mají stejné parametry.

Zamyslete se nad tím, zda se může lodička bez motoru na řece pohybovat rychleji než samotná voda. Svou odpověď zdůvodněte a předpokládejte, že proudění vody je laminární.

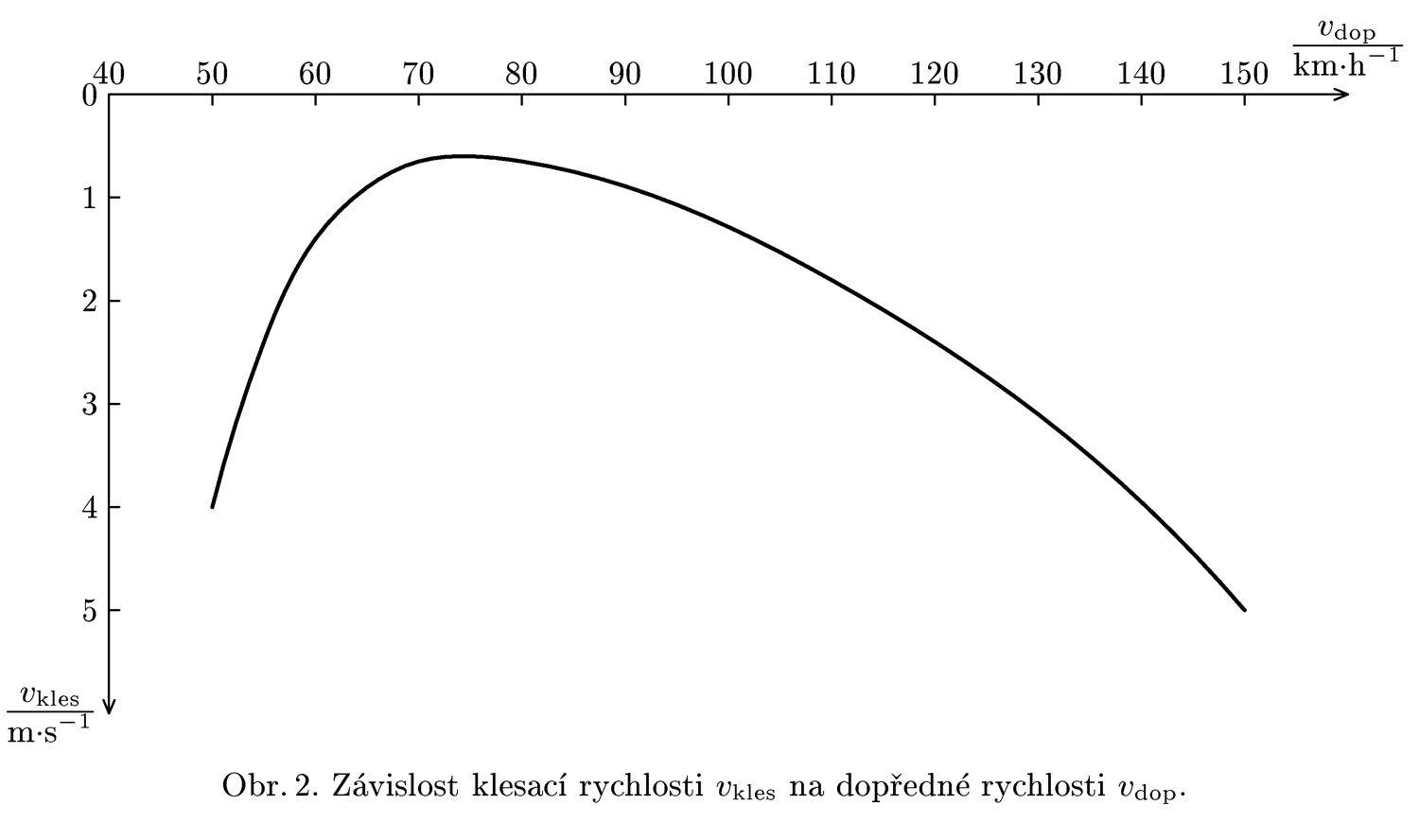
Jeden známý letec se rozhodl ve větroni přeletět kanál La Manche. V Calais se nechal vyvléci do výšky $h = 3\, \jd{km}$ a z této výšky se přímým klouzavým letem vypravil do Anglie. Jako dobrý pilot ví, kterak při ustáleném letu vypadá závislost klesací rychlosti $v_{kles}$ na dopředné rychlosti $v_{dop}$ (viz graf na obr. 2). Poraďte mu, jak rychle má letět, aby doletěl co nejdál.

Když je ve třech čtvrtinách cesty do Anglie, začne od ostrovů fučet silný vítr o rychlosti $10\, \jd{m \cdot s^{-1}}$. Rozhodněte, jak rychle má letět nyní, aby se dostal co nejdál. Jaká by musela být rychlost větru, aby mu znemožnila přistát na pevnině, případně aby mu umožnila návrat do Francie?

Mojžíš přistoupil k Rudému moři zvolav: „Rozevři se mořská hladino a nech národ vyvolených projít suchou nohou do zemi zaslíbené.“ Poté vstoupil do mořských vln a ty se rozestoupily. Určete, jak velkou silou byl obdařen Mojžíš, aby mohl převést Židy přes Rudé moře. Předpokládejte, že moře je široké 1 km a hluboké 20 m.

Planeta Utod o hustotě $ρ$ je pokryta mořem z kapaliny hustoty $ρ'$. Výška hladiny je $h$, poloměr planety $R$. Vyšetřete stabilitu planety.

Do dna vědra zhotovte malý kruhový otvor a vědro naplňte vodou. Změřte, jak závisí doba výtoku vody na počáteční výšce hladiny. Naměřené hodnoty porovnejte s teorií.

Z obdélníkové nádoby vyléváme vodu přes jednu její stěnu. Na hladině plave mrtvá moucha. Proměřte, jak se bude moucha při velmi pomalém vylévání pohybovat. Místo mrtvé mouchy můžete použít jiný odpovídající předmět.

Pokuste se spočítat, jak velká hliníková mince se ještě udrží na vodní hladině.