Vyhledávání úloh podle oboru

Matouš si vystřihl z tvrdého papíru lodičku, která je nakreslena na obr. 3 při pohledu shora. Do místa $A$ pak kápl kapičku jaru a loď spustil na vodní hladinu. Nemálo se podivil, když loď sama od sebe vyrazila prudce vpřed. Umíte pohyb lodi vysvětlit? Platí pro něj zákon zachováni energie?

Mějme válcovou nádobu se rtutí. Roztočíme ji úhlovou rychlostí $Ω$ kolem rotační osy. Určete ohniskovou vzdálenost zrcadla, které tvoří povrch rtuti.

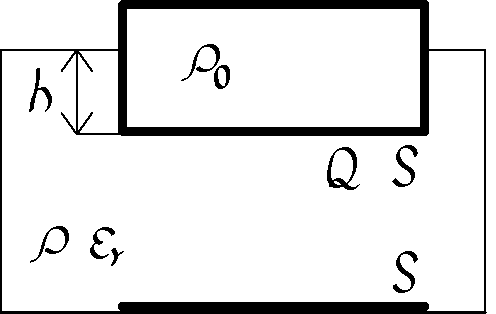
Velká nádoba je naplněna tekutým dielektrikem hustoty $ρ$ a relativní permitivity $ε_{r}$. Na dně nádoby je tenká kovová deska o ploše $S$. Nad ní plave vodivý hranol hustoty $ρ_{0}<ρ$, jehož podstava má obsah $S$. Na hranol přivedeme elektrický náboj $Q$ (viz obrázek). Jak ovlivní elektrické pole hloubku ponoru hranolu, víte-li, že

• deska na dně je uzemněna
• deska není uzemněna

Zaveďte takové zjednodušující předpoklady, abyste byli schopni úlohu řešit, a pokuste se odhadnout chybu, kterou vaše zjednodušení do výsledku vnesou.

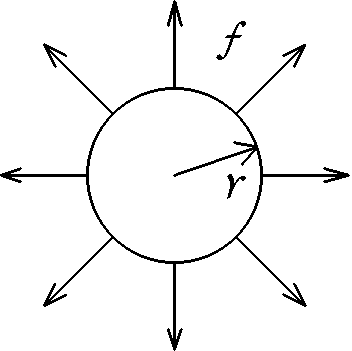
Jak moc můžete nafouknout pouťový balónek, dokud nepraskne? Předpokládejte, že balónek má tvar koule. Nenafouknutý nechť má poloměr $r_{0}$. Je z gumové blány, která má v přiblížení následující elastické vlastnosti.

Roztahujeme-li kruh vyříznutý z této blány na okraji tak, že síla na jednotku délky obvodu je $f$, bude poloměr kruhu $r$ přímo úměrný $f$, $r=r_{0}(1+af)$, $a$ je konstanta úměrnosti (viz obrázek). Materiál praskne při maximální síle na jednotku délky $f_{max}$. Na jedno nadechnutí naberete do plic objem $V_{fuk}$ vzduchu a ten pak fouknete do balónku. Kolikrát můžete do balónku fouknout, než praskne, a jaký bude mít rozměr?

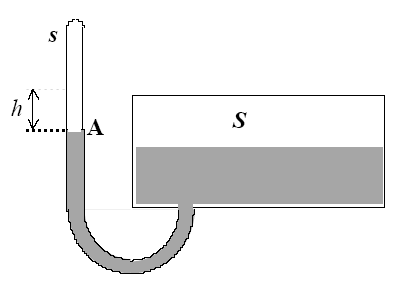
Máme soustavu kapiláry o průřezu $s$ a nádoby o vodorovném průřezu $S$, která je naplněná rtutí jako na obrázku. Z kapiláry je vyčerpán vzduch. Když uvolníme kolíček A v kapiláře, stoupne hladina rtuti v kapiláře o $h$ a v nádobě klesne o $Δh$. Jaká se při tom uvolní energie? Předpokládejte, že $S\gg s$ a $h\gg Δh$.

Křemílek a Vochomůrka mají problém. Uprostřed zimního spánku je probudil kapající vodovod, nenechal je usnout a nutil je přemýšlet na téma „kapající vodovody v současném světě“. Byl tak dotěrný, že pokud neumřeli, přemýšlejí dodnes. Zkuste doma objevit nějaký kapající vodovod, zamyslete se a poté změřte, jaké povrchové napětí vykazuje voda kapající z kohoutku.

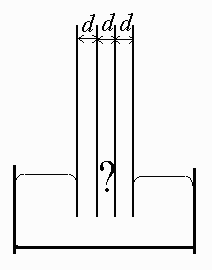
Mějme dvě tenounké trubičky, jednu o průměru $d$, druhou o průměru $3d$, přičemž menší z nich je souose vsunuta do větší (opačně by to nejspíše nešlo). Tuto soustavu ponoříme jedním koncem do misky se rtutí, jak je to vidět na obrázku. V jaké výšce se ustálí hladina rtuti uvnitř tenčí kapiláry a v mezeře mezi oběma kapilárami vzhledem k hladině v misce?

Může bitevní loď plovat ve vaně?

Máme samozřejmě na mysli dostatečně malou loď nebo dostatečně velkou vanu. V každém případě je okolo lodě málo vody v porovnání s jejím objemem (viz obr. 1). Mějme konkrétně loď o hmotnosti $100\;\textrm{tun}$ a vanu, ve které je $1\;\textrm{m}^{3}$ vody.

Pokuste se experimentálně určit hustotu vzduchu, pokud máte k dispozici dva různě velké balónky napuštěné plynem lehčím než vzduch. (Nevíme, jak je to s pouťovým šílením v této době jestliže neseženete vhodný plyn, např. vodík, zkuste použít horký vzduch – chyba měření bude ovšem ďábelská. Případně můžete měřit s plynem těžším vzduchu).

Nápověda: Neznámé hustoty náplně balónku se při výpočtu zbavíte právě tím, že provedete měření pro dva různé balónky, čili ze dvou rovnic tuto neznámou vyloučíte.

V uzavřeném skleněném zvonu je hladina rtuti a na ní plave ocelová kulička. Rozhodněte, jak se kulička pohne, pokud vyčerpáme ze zvonu vzduch.