Vyhledávání úloh podle oboru

Strýček Skrblík se jednou doslechl o perpetuech mobile a vytušil příležitost, jak ještě více zbohatnout. Vypsal grant na vymýšlení „věčných strojů“, ale jediní, kdo se přihlásili, byli jeho synovci. Přinesli strýčkovi následující tři nápady:

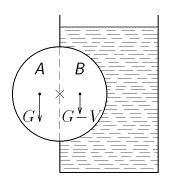
• Základem prvního perpetua je válec, který je dutý, vodotěsný a je upevněn v ose na valivých ložiscích. Obrázek nám objasní funkčnost stroje. Na obě části válce sice působí tíhová síla $G$, ale část $B$ je vůči části $A$ válce nadlehčována vztlakovou silou $V$ dle Archimédova zákona. Válec se bude otáčet a jeho rotační energii převedeme na elektrickou energii.

• Pokud zahřejeme kapalinu, zvětší svůj objem. Zároveň víme, že kapalina je nestlačitelná. Proto budeme kapalinu zahřívat a ochlazovat, změnu jejího objemu převedeme na mechanickou energii a tu na energii elektrickou. Část takto obdržené energie využijeme na zahřívání kapaliny (ochlazení kapaliny zajistí okolní prostředí, odborně „lázeň“). Zbytek energie roztočí stroje ve Skrblíkových továrnách.

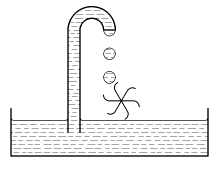
* Do nádoby s vodou je zasunuta kapilára. Díky kapilárním jevům voda naplní celou kapiláru a z horního zahnutého konce odkapává dolů, jak je to vidět na obrázku. Dole je umístěna vodní turbína, která je roztáčena padající vodou, a tak může konat práci.

Strýček se nadšeně pustil do výroby těchto strojů, jaké však bylo jeho zklamání, když zjistil, že ani jediný z nich nefunguje. Od té doby už o žádných „perpetech“ nechce ani slyšet.

Na vás teď je, drazí řešitelé, abyste se pokusili vysvětlit, proč žádný z nápadů synovců strýčka Skrblíka nemůže fungovat jako perpetuum mobile.

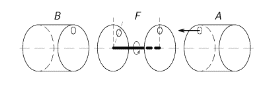
Mějme aparaturu, jejíž schéma je na obrázku. Molekuly opouštějící nádobu s plynem $A$ (teplota $T_{A}$, střední kvadratická rychlost molekul $v_{A})$ tvoří molekulární svazek, jež dále prochází rychlostním filtrem $F$. Pouze částice s rychlostí $v_{F}$ proletí až do nádoby $B$. V prostoru mezi deskami filtru je vakuum, střední volná dráha molekul je větší než rozměr aparatury. Při vhodné volbě rychlosti $v_{F}$ ($v_{F}$ > $v_{A})$ bude teplota nádoby $B$ vyšší než nádoby $A$. Tudíž teplo z tělesa chladnějšího ($A)$ bude přecházet na těleso teplejší ($B)$, což je ve sporu s druhým principem termodynamiky. Vaším úkolem je vysvětlit (ne)správnost této úvahy.

Tentokrát je vaším experimentálním úkolem změřit další fyzikální vlastnost vody, totiž její hustotu. Aby nevznikaly velké zmatky, vymysleli jsme pro vás tento postup měření: Do vody ponoříme nádobu dnem vzhůru, původně celou naplněnou vzduchem. Jak se nádoba ponořuje, tak se do nádoby postupně dostává voda. Vymyslete, jak tímto postupem zjistíte hustotu vody a pokuste se navrhnout takové experimentální uspořádání, abyste dosáhli maximální přesnosti. Znáte atmosférický tlak a tíhové zrychlení.

Jednoho krásného dne se studentíci na jednom nejmenovaném gymnáziu nudili, a tak si vymysleli zábavu. Do igelitového pytlíku nabrali vodu a vyhodili jej z okna. Na betonovém chodníku to udělalo krásný gejzír. Ale co čert nechtěl – zrovna přišel do třídy profesor fyziky a zeptal se jich: „Z jaké výšky byste museli vyhodit ten pytlík z okna, aby vám ta voda přešla do varu?“ No, a my se vás ptáme na totéž. Můžete zanedbat odpor vzduchu, popřípadě zauvažovat, co by se stalo, kdyby tam odpor vzduchu byl.

Jistě se vám už někdy stalo, že jste při vaření ukápli na mírně horkou plotýnku či pánev kapku vody. Potom jste si mohli kromě nepříjemného sykotu všimnout, že chvilku kapka poskakuje po plotýnce, a pak velice rychle zmizí. Jak to, že se menší kapka vypařuje rychleji než kapka větší?

Na ledovou plochu rybníka o teplotě $0\;^\circ\textrm{C}$ dopadne rozehřátá dělová koule o poloměru $R$, měrné tepelné kapacitě $c_{k}$ a teplotě $100\;^\circ\textrm{C}$. Jak hluboko se koule ponoří do ledu, jestliže měrná tepelná kapacita ledu je $c_{l}?$ Předpokládáme, že se veškeré teplo využije na tavení ledu.

Ve vztahu pro tepelnou vodivost $q=Q/(S\textrm{d}t)=-\lambda(\textrm{d}T/\textrm{d}x)$ u tyče spádu teploty $\textrm{d}T/\textrm{d}x$ a průřezu $S$ a se pokuste najít vyjádření pro konstantu $\lambda$, pokud tyčí projde za čas $\textrm{d}t$ teplo $Q$.

Nápověda: střední energii jedné molekuly lze vyjádřit jako $u=m_{0}c_{v}T$.

Při odvození rovnice plynu jsme neuvažovali nárazy molekul na sebe navzájem. Pokuste se říci, ve kterém bodě našich úvah je třeba tento problém diskutovat a diskutujte ho.

Nápověda: Při diskusi použijte pojem střední volné dráhy molekuly.

V místnosti stojí otevřená lednička zapojená do zásuvky a mrazí. Po jedné hodině provozu necháme teplotu v místnosti ustálit. Jak se tato teplota liší od počáteční teploty v místnosti, pokládáme-li místnost za tepelně izolovanou?

Pokuste se změřit odpor spirály elektrického vařiče.

Návod: Ohřívejte vodu vařičem a sledujte závislost její teploty na čase. Z této závislosti zjistěte výkon vařiče, ze kterého už snadno naleznete odpor spirály. Zřejmě vám už došlo, že tato úloha je takzvaně experimentální.