Vyhledávání úloh podle oboru

Na trajektu máme nezabrzděné auto, které stojí rovnoběžně s jeho osou. Trajekt je se houpe harmonicky na vlnách, tj. $φ(t)=Φ\sin(ωt)$. Maximální úhlová výchylka trajektu je Φ. Jak daleko od kraje můžeme zaparkovat auto, aby nám nemohlo spadnout do moře? Uvažujte, že maximální výchylka se pomalu zvětšuje z nuly na hodnotu Φ.

V pohádce Mrazík vyhodil Ivan loupežníkům kyje do takové výšky, že spadly až za půl roku. Jak vysoko by je musel vyhodit, aby dopadly za takovou dobu? Vytvořte první a druhý hrubý odhad. Zdůvodněte, proč jsou tyto odhady nejspíš řádově špatné. Co jste všechno zanedbali? Z jakých důvodů je celkově nesmyslné, aby kyje dopadly na prakticky stejné místo po půl roce? Nebraňte se proudu kritiky na tuto klasickou pohádku!

Pustíme z klidu z ruky kuličku o průměru $r$ ze střechy dolů. Předpokládejme, že můžeme zanedbat odpor vzduchu. Jaký se nám bude jevit poloměr této kuličky v závislosti na čase? Předpokládejme, že se na kuličku díváme přímo ze shora a že v okamžiku upuštění kuličky byla $x_{0}$ pod našima očima.

Uvažujte bombu padající volným pádem svisle dolů na cíl. Po celou dobu pohybu, který začíná z klidu, vydává vlivem tření o vzduch zvuk, který se šíří rychlostí $c=340~ \rm m\cdot s^{-1}$. Jaká je maximální možná rychlost dopadu, aby ti, na které bomba dopadne, ji ještě za živa slyšeli?

Centra měst Drážďan a Vídně jsou od sebe vzdálena zhruba $d=370\;\mathrm{km}$ vzdušnou čarou po Zemi. O co kratší by byla vzdálenost mezi nimi, pokud bychom mohli jít přímým tunelem skrz Zemi? Zanedbejte rozdíl nadmořských výšek, ve kterých jsou města položena. Na závěr můžete srovnat i délku cesty, kterou byste mezi městy jeli autem. Aby byla tato úloha jednoduchá, je zde nápověda. Goniometrické funkce můžeme pro malé úhly aproximovat (tedy přiblížit) jako $$ \mathrm{sin} α ≈ α - α^{3}/6 \,,\\ \mathrm{cos} α ≈ 1 - α^{2}/2 \,,\\ \mathrm{tg} α ≈ α + α^{3}/3 \,, $$ kde úhel dosazujeme v radiánech. Toho můžeme využít pro vyjádření neznámé v rovnici, kde vystupuje jak samotný úhel, tak i obsažený v nějaké goniometrické funkci.

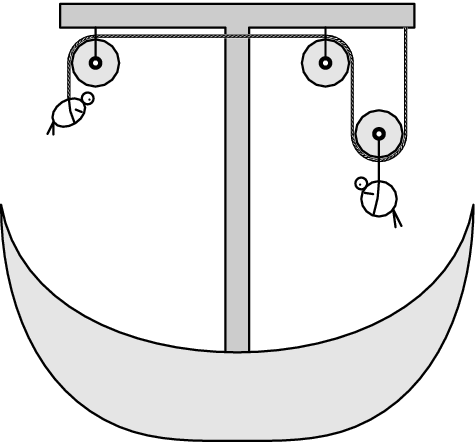
Dva mladí, ale bohužel poněkud prostorově výraznější, Benátčané Paolo a Francesca Muschetti (o hmotnostech $m_{P}=180\;\mathrm{kg}$ a $m_{F}=130\;\mathrm{kg}$) by se chtěli spolu projet na gondole. Žádný gondoliér je ale nechce vzít na svou loď, protože ví, že by je všechny tři loď neunesla. Chytrý gondoliér Jacopo ale vymyslel rampu, na kterou umístil tři kladky dle obrázku. Skrz kladky provlékl lano a oba mladé Benátčany na ně upevnil, viz obrázek – každého na opačný konec, tak, že nejprve byla nahoře lehčí Francesca a po jisté chvíli ji v této pozici vystřídal těžší Paolo. Jak vysoká musí být rampa, aby gondola stihla přejet přes kanál? Doba jízdy je $τ=60\;\mathrm{s}$. Přepokládejme, že při použití tohoto zařízení se již gondola nepotopí. Zanedbejte veškeré tření, hmotnost lana a momenty setrvačnosti kladek.

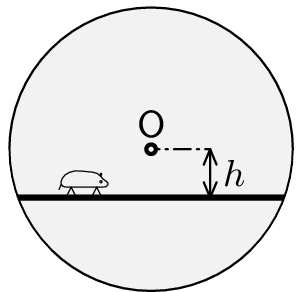
Rado si pro svého křečka Bobka přichystal speciální kolečko. Celá soustava se může otáčet okolo osy procházející bodem $O$, který je středem kolečka, a ke kolečku je vodorovně připojená deska ve vzdálenosti $h$ od osy rotace, viz obrázek. Jak se má křeček Bobek pohybovat po desce, aby deska zůstala po celou dobu pohybu vodorovně? Koeficient tření mezi křečkem a deskou je $f$.

Mějme dvě auta o stejné hmotnosti jedoucí proti sobě rychlostí $v_{0}$. V jaké vzdálenosti musí začít brzdit, aby nedošlo ke srážce? Uvažujte dva případy, kdy auta jedou proti sobě na rovině a kdy auta jedou po silnici se sklonem $α$. Víte, že oba řidiči začnou brzdit v týž okamžik a velikost brzdné síly každého auta je $f\cdot N$, kde $N$ je složka tíhy automobilu kolmá na silnici.

Máme malý míček o poloměru $r$ těsně nad míčem o poloměru $R$. Nejspodnější bod spodního míče je ve výšce $h$ nad zemí. Oba míčky pustíme. Do jaké nejvyšší výšky může vystoupit horní míček? Uvažujte, že všechny srážky jsou dokonale pružné. Bez újmy na bodech můžete považovat hmotnost horního míčku za zanedbatelnou.

Bonus: Postup zobecněte na $N$ míčků. (Stále můžete uvažovat, že hmotnost míčku výše je zanedbatelná oproti míčku pod ním.)

Odhadněte, jakou minimální energii musíme dodat kosmické stanici, abychom ji dostali na oběžnou dráhu. Můžete pracovat s hodnotami pro mezinárodní kosmickou stanici ISS, která obíhá Zemi ve výšce cca $h=350\;\mathrm{km}$ a má celkovou hmotnost přibližně $m=450\;\mathrm{tun}$. Vysvětlete, proč je odhad minimální a vyjmenujte alespoň některé fyzikální skutečnosti, které vedou k tomu, že je skutečná spotřeba raket významně vyšší.