Vyhledávání úloh podle oboru
Databáze úloh FYKOSu odjakživa
astrofyzika (85)biofyzika (18)chemie (24)elektrické pole (71)elektrický proud (76)gravitační pole (81)hydromechanika (146)jaderná fyzika (44)kmitání (57)kvantová fyzika (31)magnetické pole (43)matematika (89)mechanika hmotného bodu (298)mechanika plynů (87)mechanika tuhého tělesa (221)molekulová fyzika (72)geometrická optika (78)vlnová optika (65)ostatní (167)relativistická fyzika (37)statistická fyzika (21)termodynamika (155)vlnění (51)
termodynamika
2. Série 9. Ročníku - P. Lomonosův průvan
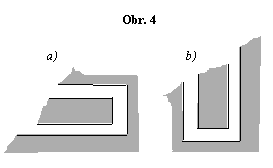
Velký přírodovědec M. V. Lomonosov studoval ve své světově proslulé práci „O volném pohybu vzduchu v dolech“ závislost směru proudění vzduchu na ročním období. Po dlouhém a strastiplném bádání dospěl k závěru, že teplota vzduchu je v dole stále stejná po celý rok. (V jeho době byly doly ještě poměrně mělké.) Určete, jakými směry bude vzduch proudit v létě a v zimě v dolech umístěných podle obr. 4.
2. Série 9. Ročníku - S. Mayerův vztah
Jde o úlohu jednoduchou, ale pokud ji budete chtít řešit, radši si ještě jednou přečtěte text seriálu (i když vás možná trochu nudí) a pokud příklad zdárně vyřešíte, určitě pochopíte, o co v tomto díle seriálu šlo. Tedy:
Odvoďte, jak vypadá 1. věta termodynamická pro izochorický děj ($V=\;\mathrm{konst})$ a určete tím, co znamená výraz $c_{v}=1/n\cdot dU/dT$.
Výsledek po dosazení do jedné z výše uvedených rovnic (snadno naleznete které), nazýváme Mayerovým vztahem.
1. Série 9. Ročníku - 4. tlak plynu
V nádobě, jejíž stěny mají teplotu $t_{c}$, se nachází plyn o teplotě $t$. V kterém případě bude tlak na stěny nádoby větší: $t>t_{c}$ nebo $t<t_{c}?$
5. Série 8. Ročníku - E. chladnutí kapalin
Ve fyzice se často zkoumají tzv. relaxační procesy, tj. postupné ustálení určité fyzikální veličiny na nějaké hodnotě. V termodynamice pod pojmem relaxační doba máme na mysli čas, za který nastane mezi sledovaným systémem a jeho okolím (s nějakou přesností, danou chybou měření nebo fluktuacemi) termodynamická rovnováha. Relaxační doba se samozřejmě mění od procesu, který sledujeme – při vyrovnání tlaků je to asi $10^{-16}\; \textrm{s}$, při různých chemických dějích až měsíce či roky.
Vaším úkolem bude sledovat rychlost chladnutí dvou či více kapalin (např. voda a olej) za stejných okolních podmínek. Aby se vaše práce více podobala skutečnému fyzikálnímu experimentu, proložte naměřenými hodnotami funkci $f(t)=Ae^{-Bt}+T_{0}$ a zkuste interpretovat vypočtené konstanty nebo alespoň odhadněte, na čem by mohly záviset. Pro ty, kdo neví, co je to lineární regrese, je určen krátký odstavec o této metodě.
4. Série 8. Ročníku - 2. jak asi táhne komín
Vertikální roura výšky $h=1\;\mathrm{m}$ s plochou podstavy $S=50\;\mathrm{cm}^{2}$ je z obou stran otevřená. V dolní části roury se nachází ohřívač o výkonu $N=100\; \textrm{W}$. Jaká bude rychlost proudění vzduchu v troubě? Lze předpokládat, že veškerý tepelný výkon ohřívače se spotřebuje na ohřátí vzduchu. Atmosférický tlak je $p_{0}=100\; \textrm{kPa}$, teplota okolního vzduchu $t=20\;\mathrm{°C}$. Molární tepelná kapacita vzduchu při konstantním objemu je $C_{V}=2,5\; \textrm{R}$, kde $R$ je plynová konstanta.
3. Série 8. Ročníku - 3. polytropa na zahřátí
Pod pojmem polytropický rozumíme v termodynamice proces charakterizovaný rovnicí $pV^{α}=\;\mathrm{konst.}$, kde $α$ je daný parametr. Pro vhodné $α$ dostáváme např. izobarický ($α=0$), izotermický ($α=1$) nebo izochorický ($α=∞$) děj. Mějme nejjednodušší případ ideálního jednoatomového plynu. Při jakém polytropickém ději (t.j. pro jakou hodnotu $α$) se v něm zachovává
- počet srážek atomů v jednotce objemu
- celkový počet srážek?
2. Série 8. Ročníku - 3. nehoda ve vakuu
Dva kosmonauti se nacházejí v otevřeném mezihvězdném prostoru. Neočekávaně dojde k přetržení přívodní hadice u jednoho z nich a následně úniku veškerého vzduchu ze skafandru. Jeho přítel duchaplně připojí ventil ze svého skafandru na utržený konec hadice. Jenže ouha! Hadice je ucpaná a ke zprůchodnění trubice je třeba přetlaku alespoň $1,1\; \textrm{atm}$. Přitom standardní tlak udržovaný přístroji ve skafandru je roven $1\; \textrm{atm}$. Rozhodnou se k následujícímu kroku: vypnou přívod vzduchu nepoškozeného skafandru a společně se vystaví velmi intenzivnímu záření blízké hvězdy, čímž se jejich teplota zvýší z původních $27^{\circ}\;\textrm{C}$ na $107^{\circ}\;\textrm{C}$. Po vyrovnání tlaku rozpojí hadice a rychle se vrátí do stínu solárního článku, kde jejich teplota klesne k normálu. Jakého tlaku dosáhnou touto operací v poškozeném skafandru?
Poznámka: Komu se zdá tato příhoda příliš fantastická nebo málo vědecká, může stejnou úlohu počítat pro dvě identické nádoby spojené hadicí s jednosměrně propustnou klapkou.
6. Série 7. Ročníku - 1. kombinézy
V Arktidě se potkali dva polárníci, vybaveni různými druhy kombinéz. Při bližším seznamování se ukázalo, že teplota na povrchu kombinézy prvního polárníka je vyšší než u jeho kolegy. Která z kombinéz je teplejší, tj. má lepší izolační vlastnosti?
2. Série 7. Ročníku - E. vzdušná kapacita
Pomocí elektrického vysoušeče vlasů (zkráceně f.é.n.) změřte měrnou tepelnou kapacitu vzduchu.
Poznámka: Dbejte všech bezpečnostních zásad při práci s elektrickými zařízeními, viz ing. František Soukup: Elektřina nepromíjí, Práce – nakladatelství ROH, Praha 1955 (zejm. str. 19–21, 107 a celá kapitola Amatérství-fušérství).
2. Série 2. Ročníku - 4. výška sloupce vzduchu
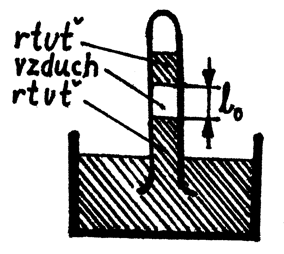
Barometrická stupnice
V barometrické trubici je sloupec vzduchu. Při teplotě $t_{0}=10^{\circ}\;\mathrm{C}$ je výška sloupce $l_{0}=10\;\mathrm{cm}$. Jaká bude jeho výška při teplotě $t=30^{\circ}\;\mathrm{C}$?