Vyhledávání úloh podle oboru

Vezmeme-li astronomické ročenky za posledních $100$ let, zjistíme, že slunečních zatmění je přibližně $1,5$krát více než zatmění měsíčních. Zkuste přijít na to, proč je tomu tak.

Kolik elektronů je ve vodivostním pásu ($E ≥ 0$) nepříměsového polovodiče se šířkou zakázaného pásu $0,6 \,\jd{eV}$? V příkladu byla ilustrována závislost vodivosti polovodiče s donorovou příměsí na teplotě. Jak se bude chovat polovodič s akceptorovou příměsí? Je-li v čase $t=0$ excitováno $n_{e}(0)$ elektronů do vodivostního pásu, bude jejich počet klesat exponenciálně, konkrétně bude platit $n_{e}(t)=n_{e}(0)$ exp(−$t/τ_{e})$. Když budeme excitovat od okamžiku $t=0$ za jednotku času $c_{e}$ elektronů, tvrdili jsme, že se počet elektronů ve vodivostním pásu změní o hodnotu $c_{e}$ $τ _{e}$ (viz vztah 1 v seriálu). Na vás je, abyste tento vztah dokázali.

Sežeňte si tenké gumičky a

• změřte závislost protažení gumičky na působící síle a sestrojte graf naměřené závislosti,
• změřte také sílu, při které gumička praskne,
• zatižte gumičku co nejvíce (ale tak, aby se nepřetrhla) a po sundání zátěže proveďte znovu měření a).

Změřte mez pevnosti nitě v tahu. S řešením nám pošlete $1\,\jd{ m}$ dlouhý vzorek vaší nitě.

Pokuste se změřit, jak tlustý je list papíru. Aby byly vaše výsledky srovnatelné, měřte papír pocházející ze školního sešitu nelinkovaného.

Teď už nebude sněžit, a proto můžete pozorovat déšť. Pokuste se změřit objem jedné dešťové kapky. Nezapomeňte si zapsat, kdy to vlastně pršelo a jestli déšť přišel ze západu nebo z východu (porovnávejte kvalitu východních a západních dešťů). Např. při pádu padákem lze měřit šuplerou všechny rozměry kapky, ocejchujeme-li si dalekohled, můžeme v něm odhadovat velikost kapek…

Představte si, že jdete večer klidně spát a do rána se veškeré vzdálenosti a rozměry všech přemetů zvetší desetkrát, přičemž jejich hmotnost se nezmění. Zanechá tato událost nějaké stopy na vaší existenci? A pokud ano, tak jaké?

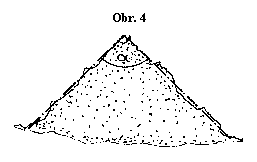
Sypeme-li prášek (suchý písek, mouku a podobně) volně na jedno místo, vznikne kužel s vrcholovým úhlem (viz obr. 4). Pokuste se změřit tento úhel pro různé látky. Umíte výsledky měření nějak odůvodnit?

Napište (a zašlete) program, který určí všechny kořeny polynomu. S jeho pomocí nalezněte čtyři řešení rovnice $x^{4}+2x^{3}+5x^{2}–4x+3=0$.

Sestavte program pro iterační metodu a zvolte vhodnou konstantu $k$ pro fci $g$, abyste dostali vhodný interval okolo 1 splňující kontraktivnost. Ověřte lineární konvergenci a zkuste zjistit míru zrychlení při užití Aitkinova procesu.