Vyhledávání úloh podle oboru
Databáze úloh FYKOSu odjakživa
astrofyzika (85)biofyzika (18)chemie (24)elektrické pole (71)elektrický proud (76)gravitační pole (81)hydromechanika (146)jaderná fyzika (44)kmitání (57)kvantová fyzika (31)magnetické pole (43)matematika (89)mechanika hmotného bodu (298)mechanika plynů (87)mechanika tuhého tělesa (221)molekulová fyzika (72)geometrická optika (78)vlnová optika (65)ostatní (167)relativistická fyzika (37)statistická fyzika (21)termodynamika (155)vlnění (51)
mechanika hmotného bodu
1. Série 23. Ročníku - 3. adiabatický invariant
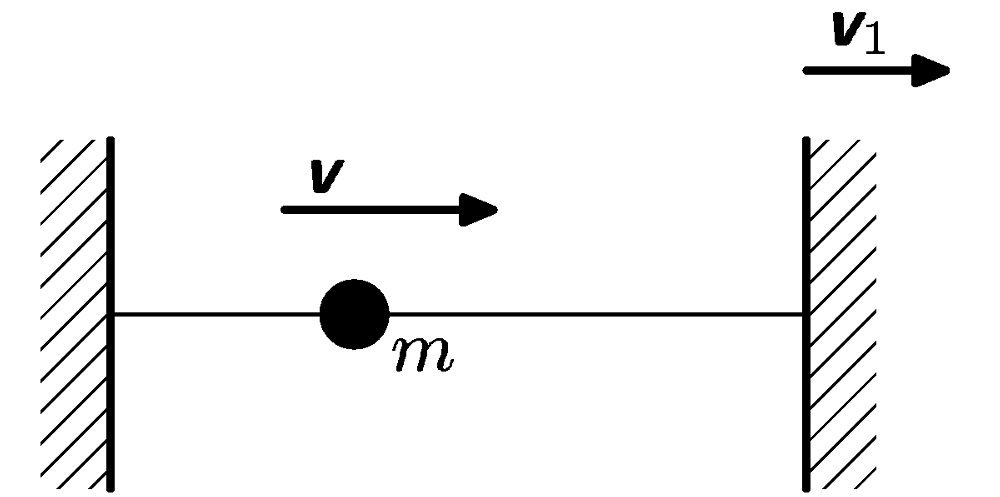
Mezi dvěma zarážkami se po přímce rovnoměrně pohybuje hmotný bod o hmotnosti $m$ rychlostí $v$. Jednu ze zarážek začneme oddalovat rychlostí $v_{1}<<v$. Jak se změní energie hmotného bodu?
Na Zajímavé teoretické fyzice nespala Janap.
3. Série 22. Ročníku - 2. trainstopping
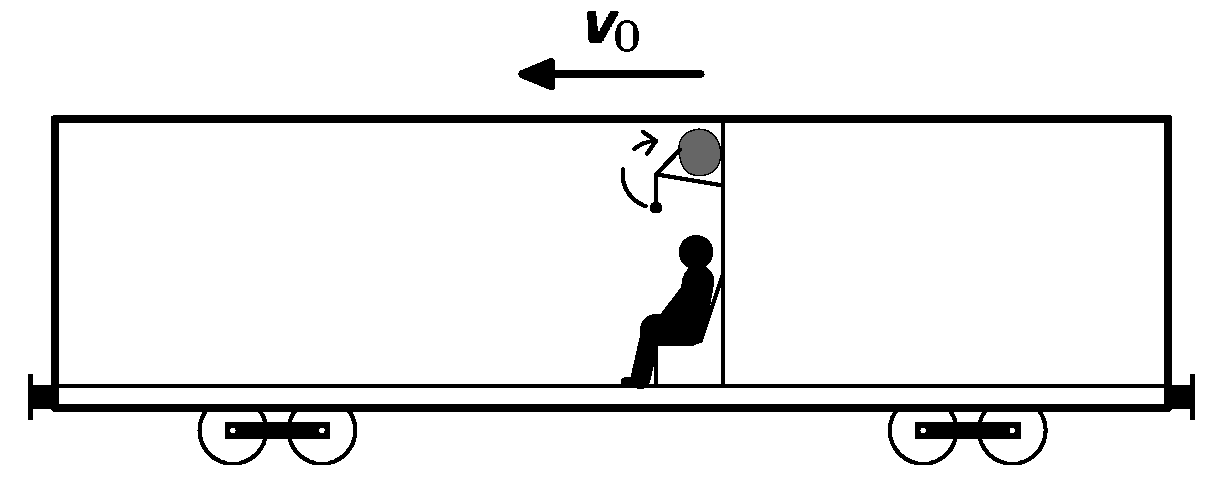
Honza jede domů vlakem rychlostí $v_{0}$. Z poličky na zavazadla mu z batohu visí olovnice. Najednou vlak začne brzdit (zrychlením $a$ po dobu $t)$, protože na železniční přejezd před ním vjel neopatrný řidič. A Honzu napadne – mohla se olovnice s napnutým provázkem otočit o 180 °? Uvažte, že je olovnice pevně zavěšena na poličce.
Z maďarské přípravy na FO od Dalimila vybral Aleš.
2. Série 22. Ročníku - 3. ledvinové koule
Malá koule stojí v klidu na velké kouli, která volně leží na podložce. Do malé koule nepatrně strčíme a ta se svalí na zem. Jak daleko od původního bodu dotyku velké koule se zemí malá koule dopadne?
na teoretické mechanice zkoulel Lukáš Ledvina
2. Série 22. Ročníku - E. šikmá věc
Kolik vody musí být v PET lahvi postavené na uzávěr, aby její stabilita byla největší (při vychýlení ze svislé polohy spadne ze nejdelší čas)? Nezapomeňte na teoretickou předpověď.
nad vypitou lahví se zamyslel Béda
1. Série 22. Ročníku - 1. klouzání a kmitání
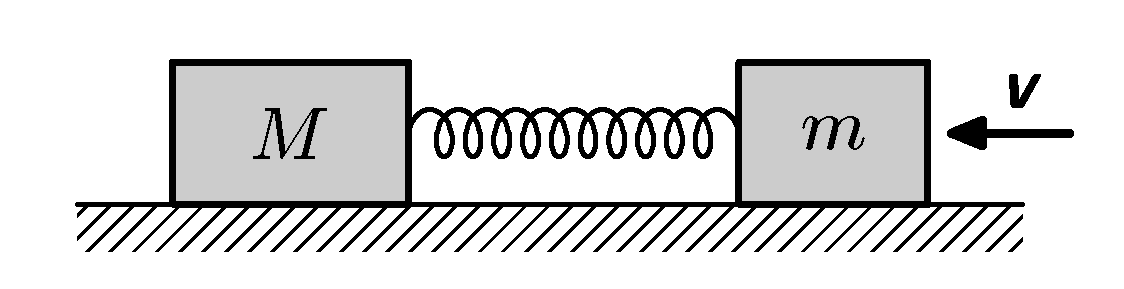
Dvě závaží o hmotnostech $m$ a $M$ jsou spojena pružinou o tuhosti $k$ a leží na hladké podložce (tření můžeme zanedbat). Tělesu $m$ udělíme rychlost $v$ (viz obrázek). Jaká bude nejkratší vzdálenost mezi tělesy a kdy jí dosáhnou?
V ročenkách kanadské FO našel Honza Prachař.
6. Série 21. Ročníku - 1. pterodaktyl sestřelen
Pták FYKOSák letěl v létě 2007 na prázdniny do Jižní Ameriky. Svůj výlet dlouho plánoval, chtěl obletět celý kontinent, zhlédnout husté amazonské pralesy, zasněžené vrcholky And, patagonské nížiny i poušť Atacama, jezero Titicaca a pláž Copacabana. Cesta však dopadla tragicky, pták FYKOSák se už nikdy nevrátil.
Když letěl nad kolumbijskými pralesy, byl mylně považován za tajného agenta CIA a upadl do zajetí Revoluční ozbrojené lidové armády Kolumbie (FARC). Již téměř rok je pterodaktyl uvězněný kdesi v zajateckém táboře uprostřed kolumbijské džungle, strádá hladem a steskem. Za jeho propuštění požaduje FARC vysoké výkupné. Pokud bychom ho chtěli zaplatit, museli bychom zrušit soustředění a možná i celý seminář na několik let.
Dejte své chytré hlavy, silné paže a odvahu dohromady a pomozte nám vysvobodit ptáka FYKOSáka!
Pterodaktyl letěl ve výšce $1\,\jd{ km}$ nad pralesem rychlostí $4\,\jd{ m ⁄ s}$. Guerillový válečník, držící v ruce kalašnikov (kulka opouští hlaveň rychlostí $710\,\jd{ m ⁄ s}$), ho spatřil nad hlavou a vystřelil. Pták FYKOSák byl trefen do křídla a začal padat. Jak daleko od válečníka dopadl? (Odpor vzduchu si dovolte zanedbat.)
Vyplodil Honza Prachař.
6. Série 21. Ročníku - 4. rychlý úprk
Pták FYKOSák statečně prchá chodbou (nemůže v ní letět), v patách má dva vojáky, kterým se před okamžikem vymkl z pout. Chodba zatáčí ve tvaru písmene L a pterodaktyl horlivě přemýšlí, jak dál.
Chodba je široká $b$, pterodaktyl běží rychlostí $v_{0}$ a zatáčka je ve vzdálenosti $d$. Pokud velikost ptákova zrychlení dosáhne hodnoty $a_{0}$, pterodaktyl uklouzne, spadne a bude chycen. Po jaké dráze má běžet a jak se má naklánět, aby ho zatáčka zdržela co nejméně?
Napadlo Honzu Jelínka při dobíhání tramvaje za rohem.
5. Série 21. Ročníku - 2. otázka přežití
Od vchodu vede k vnitřnímu povrchu žebřík. Již jsi po něm sestoupil kilometr, když vtom jsi neopatrně sklouzl a pustil se žebříku. Jakou rychlostí dopadneš na povrch Rámy a za jak dlouho? Máš šanci přežít?
Martin Formánek
5. Série 21. Ročníku - 3. schody z nebe
Žebřík vede jen dva kilometry na plošinu, ze které se dále sestupuje po schodech, jež se mohutným obloukem klenou nad krajinou. Schodiště má zvláštní tvar. Je totiž postavené tak, že se na každý krok vynaloží stejná práce. Odvoď, jak závisí výška schodu na vzdálenosti od osy Rámy, pokud je délka schodů konstantní. Také můžeš určit, jaký tvar má onen oblouk.
Martin Formánek
5. Série 21. Ročníku - P. rámatřesení
Úspěšně ses dostal na povrch Rámy. Z ničeho nic se Ráma několikrát otřásl a zdá se ti, že se změnila rychlost jeho rotace. Tato otázka tě velice tíží. Navrhni proto několik způsobů, jak bys změněnou periodu rotace určil.
Martin Formánek