Vyhledávání úloh podle oboru

Dvě láhve, jednu plnou vody a jednu prázdnou, necháme kutálet po nakloněné rovině. Která se skutálí rychleji? Pokud ty samé láhve vyšleme se stejnou počáteční rychlostí po nakloněné rovině nahoru, která se dokutálí výše?

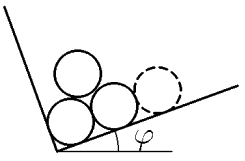
Nákladní auto bylo naloženo stejnými hladkými kládami. Před jejich vykládkou zastavilo tak, že pravými koly stojí o poznání výše než levými (příslušná přední a zadní kola jsou ovšem ve stejné výšce). Řekněme, že rovina nákladního prostoru svírá s horizontální rovinou úhel $φ$, viz obrázek. Po vykládce zbyly na autě tři klády tak, jak je na obrázku nakresleno plnou čarou. Na jakou hodnotu by se musel snížit úhel $φ$, aby se klády přeuspořádaly tak, že by ležely vedle sebe? Jakékoli tření zanedbejte.

Hokejista jede po ledě jen po jedné brusli. Led, který má hustotu $0,9\,\jd{ g\cdot cm^{-3}}$ pod bruslí taje do hloubky $h=0,03\;\mathrm{mm}$. Nůž brusle je široký $d=2\;\mathrm{mm}$. Skupenské teplo tání ledu je $λ=3,3\cdot 10^{5}\, \jd{J.kg^{-1}}$. Spočtěte velikost třecí síly mezi bruslí a ledem. Tepelnou vodivost ledu zanedbejte.

Tyč o hustotě $ρ_{1}$ a délce $l$ je za jeden konec pohyblivě připevněna k vodorovné hrazdě (tak, že se okolo ní může tyč volně otáčet), druhý konec volně visí. Pokud budeme pomalu spouštět hrazdu dolů, bude se tyč přibližovat k hladině vody ($ρ>ρ_{1}$) a začne se do ní ponořovat. Zjistěte závislost úhlu, který svírá tyč se svislým směrem, na výšce hrazdy nad hladinou.

Krychle o hraně $a$ z materiálu o hustotě $\rho_{1}$ plave v kapalině o hustotě $ρ_{2}$. Určete, v jaké poloze se krychle ustálí.

Změřte tloušťku lidského vlasu více metodami, výsledky a chyby jednotlivých metod porovnejte. Vzorek vlasu přiložen.

Sežeňte si několik (cca 6) předmětů kulového tvaru. Může jít například o míček na pingpong, tenis, fotbalový míč, ocelovou kuličku, hliněnou kuličku… Změřte jejich momenty setrvačnosti. Navrhněte a proveďte další měření s jejichž pomocí budete moci určit, zda se jedná o dutou nebo plnou kouli.

U každého výtahu v mrakodrapu je jisté riziko, že se zpřetrhají všechna lana, na kterých visí. Abychom předešli případnému úrazu, můžeme výtah vylepšit: Spodní část výtahové šachty utěsníme tak, abychom zamezili úniku vzduchu. Také okolo kabiny výtahu dáme těsnění. Výtah, který se utrhne v horním patře mrakodrapu se zabrzdí o vzduchový polštář, který si pod sebou stlačí. Předpokládejte, že kabina vážící $1000\,\jd{ kg}$ se utrhla $87\,\jd{ m}$ vysoko a vzduchotěsná část výtahové šachty začíná $15\,\jd{ m}$ nad zemí. Jak vysoko nad zemí se kabina nakonec zastaví? Jak velké síly působí po dobu pádu na cestující? V případě výpočtu síly se spokojíme i s kvalifikovaným odhadem, přesný výpočet bude po zásluze odměněn.

Vzdálenost mezi osou předního a zadního kola motocyklu je $d=1,4\;\mathrm{m}$, jejich poloměr je $r=0,3\;\mathrm{m}$ a koeficient tření mezi pneumatikami a silnicí je $f=1$. Těžiště motocyklu je uprostřed mezi osami, ve výšce $h=0,8\;\mathrm{m}$ nad zemí. Spočtěte minimální brzdnou vzdálenost pro počáteční rychlost motocyklu $v=60\;\mathrm{km} \cdot \mathrm{h}^{-1}$, jestliže řidič používá

• jen zadní brzdu
• jen přední brzdu
• obě brzdy

Zamyslete se nad získanými výsledky a zkuste je porovnat s vaší zkušeností.

Roztržitý výletník zaparkoval své auto na kopci se sklonem $\alpha=10^{\circ}$ a zapomněl jej zabrzdit. Jaké maximální rychlosti auto dosáhne? Parametry auta jsou: hmotnost $m=1200\;\mathrm{kg}$, výkon $P=55\,\jd{kW}$, maximální rychlost na rovné silnici $v_{max}=140\;\mathrm{km} \cdot \mathrm{h}^{-1}$. Předpokládejte že, odpor automobilu je úměrný druhé mocnině rychlosti.