Vyhledávání úloh podle oboru
Databáze úloh FYKOSu odjakživa
astrofyzika (85)biofyzika (18)chemie (24)elektrické pole (71)elektrický proud (76)gravitační pole (81)hydromechanika (146)jaderná fyzika (44)kmitání (57)kvantová fyzika (31)magnetické pole (43)matematika (89)mechanika hmotného bodu (298)mechanika plynů (87)mechanika tuhého tělesa (221)molekulová fyzika (72)geometrická optika (78)vlnová optika (65)ostatní (167)relativistická fyzika (37)statistická fyzika (21)termodynamika (155)vlnění (51)
mechanika plynů
(7 bodů)0. Série 31. Ročníku - 4. au to bolí
Představte si, že atmosféru Země zcela nahradíme golfovými míčky. Jaká musí být jejich koncentrace, aby měl tento „golfový plyn“ stejnou termodynamickou teplotu a stejný tlak, jako naše současná atmosféra?
Bonus: Uvažujte, že vlastnosti plynu se s výškou mění (jako u skutečné atmosféry).
(7 bodů)6. Série 30. Ročníku - 4. zastřel si svého potkana
Mirek by rád zastřelil potkana, kterého vídá na kolejích. Připravil si tedy jednoduchou vzduchovou pušku, kterou si můžeme modelovat jako trubku s konstantním průřezem $S=15\;\mathrm{mm}$ a délkou $l=30\;\mathrm{cm}$, která je na jedné straně uzavřená a na druhé otevřená. Do ní se chystá Mirek umístit náboj hmotnosti $m=2\;\mathrm{g}$, který trubku akorát utěsní, a to ve vzdálenosti $d=3\;\mathrm{cm}$ od uzavřeného konce. Náboj zde zatím nechá upevněný v klidu a natlakuje uzavřenou část trubky na určitý tlak $p_{0}$. Posléze náboj uvolní. Chce aby na konci ústí byla minimálně rychlost náboje $v=90\;\mathrm{m}\cdot \mathrm{s}^{-1}$. Poraďte mu, na jaký tlak by musel vzduchovou pušku natlakovat, aby náboj vyšel s takovou rychlostí, pokud by plyn byl ideální, a diskutujte realističnost uspořádání. Předpokládejte, že náboj je uvolňován kvazistatickým adiabatickým dějem, kde $κ=7/5$, protože se jedná o dvouatomový plyn. Uvažujte, že z vnějšku působí na náboj atmosférický tlak $p_{a}=10^{5}\;\mathrm{Pa}$. Zanedbejte energetické ztráty vyvolané třením, odporem vzduchu a stlačováním plynu před nábojem.
Karel chtěl zjistit, jestli by řešitelé zvládli přijímací řízení na magisterské studium na Matfyz.
(8 bodů)5. Série 30. Ročníku - 5. pouťový balónek
Máme balónek s hmotností (po nafouknutí) $m$ a objemem $V$ naplněný héliem, na kterém je přivázaná (prakticky nekonečná) stužka s délkovou hustotou $τ=10\;\mathrm{g}\cdot\mathrm{m}^{-1}$. Předpokládejte izotermickou atmosféru, pro níž je závislost atmosférického tlaku $p$ na výšce $z$ daná vztahem $p=p_0 \mathrm{e}^{-z/z_0}$, ($z_{0}$ je parametr atmosféry). Balónek položíme k zemi a poté ho uvolníme. Do jaké maximální výšky balónek vyletí?
(8 bodů)4. Série 30. Ročníku - 4. plynový stroj
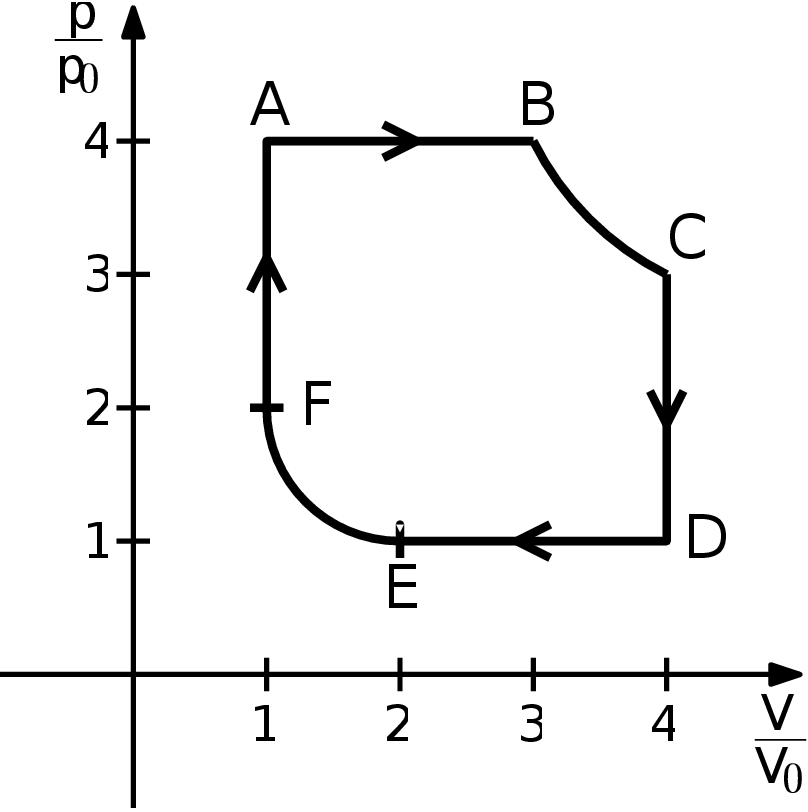
Mějme tepelný stroj naplněný ideálním plynem složeným z dvouatomových molekul. Tento tepelný stroj vykonává kruhový děj $\mathrm{ABCDEFA}$ (viz obrázek), tedy skládá se z šesti dějů
- $\mathrm{A} \longrightarrow \mathrm{B}$ - izobarické zahřátí ze stavu $4p_{0}$ a $V_{0}$ (teplotu v A označme jako $4T_{0}$) do stavu s objemem $3V_{0}$,
- $\mathrm{B} \longrightarrow \mathrm{C}$ - izotermická expanze na objem $4V_{0}$,
- $\mathrm{C} \longrightarrow \mathrm{D}$ - izochorické ochlazení na tlak $p_{0}$,
- $\mathrm{D} \longrightarrow \mathrm{E}$ - izobarické ochlazení na objem $2V_{0}$,
- $\mathrm{E} \longrightarrow \mathrm{F}$ - izotermická komprese na objem $V_{0}$,
- $\mathrm{F} \longrightarrow \mathrm{A}$ - izochorické zahřátí na tlak $4p_{0}$. Určete zbývající stavové veličiny ve stavech $\mathrm{B}$, $\mathrm{C}$, $\mathrm{D}$, $\mathrm{E}$ a $\mathrm{F}$, maximální a minimální teplotu ideálního plynu v průběhu děje (v násobcích $T_{0}$), teplo přijaté či odevzdané plynem v jednotlivých dějích a účinnost tepelného stroje. Srovnejte tuto účinnost s účinností Carnotova stroje pracujícího se stejnými maximálními a minimálními teplotami. Pro jednoduchost uvažujte, že se nemění látkové množství plynu ve stroji a nedochází v něm k chemickým přeměnám.
Bonus: To samé proveďte pro jednodušší cyklický „čtvercový“ děj, tedy $\mathrm{ABCDA}$, kde plyn začíná ve stavu $p_{0}$, $V_{0}$ a $T_{0}$ a izochoricky se ohřeje na $4p_{0}$, izobaricky se zahřeje a rozepne na $4V_{0}$, izochoricky ochladí na $p_{0}$ a izobaricky se ochladí na $V_{0}$. Srovnejte účinnosti těchto dvou tepelných strojů a diskutujte, který je lepší.
Karlovi bylo střídavě teplo a zima.
(7 bodů)2. Série 30. Ročníku - 5. várnice potřetí
Uvažujte klasickou várnici s kohoutkem dole a se vzduchotěsným víkem nahoře. Kolik čaje je možné si nalít, než budeme muset otevřít ventil, který vyrovná tlak vzduchu nad čajem s okolním tlakem?
Lukáše na soustředění trápilo, kolik čaje má být ve várnici.
(9 bodů)2. Série 30. Ročníku - P. efektivní (ná)stroj
Palné zbraně jsou vlastně takovými tepelnými stroji. Spočítejte jaká je účinnost nějaké pušky nebo pistole. (Jde o využití energie střeliva pro pohyb kulky.)
Michal původy svých nápadů raději nesděluje.
(8 bodů)1. Série 30. Ročníku - P. nebe padá na hlavu
Už jste se někdy zamysleli nad tím, proč mraky nespadnou na zem, když jsou z vody, která má přece výrazně větší hustotu než vzduch? Dešťové kapky dopadnou na zem v řádech minut, tak proč ne i mraky? Zkuste tuto skutečnost fyzikálně objasnit. Veškerá svá tvrzení podložte výpočtem.
Mirek se zadíval na nebe a dostal strach.
(6 bodů)6. Série 29. Ročníku - S. závěrečná
- Najděte v tabulkách nebo na internetu, jak se změní entalpie a Gibbsova energie při reakci
$$2\mathrm{H}_2 + \mathrm{O}_2 \longrightarrow 2\mathrm{H}_2\mathrm{O}\, ,$$ kde jde o přeměnu plynů na plyn a odehrává se při standardních podmínkách. Vypočítejte také, jak se změní entropie při takovéto reakci. Výsledky udávejte vztažené na jeden mol.
- Pro fotonový plyn platí, že tok energie skrze plochu je dán vztahem
$$j=\frac{3}{4}\frac{k_{\mathrm{B}}^4 \pi^2}{45 \hbar^3 c^3}cT^4\, .$$ Dosaďte hodnoty konstant a porovnejte výsledek se Stefanovým-Boltzmannovým zákonem.
- Vypočítejte vnitřní energii a Gibbsovu energii fotonového plynu. Dále pomocí vnitřní energie vypočítejte závislost teploty fotonového plynu na objemu při adiabatickém rozpínaní, tedy při procesu s $\delta Q=0$.
Nápověda: Zákon pro adiabatický děj s ideálním plynem jsme odvodili v druhém dílu seriálu.
- Vezměme si fotonový plyn. Ukažte pro $\delta Q/T$, že pokud ho vyjádříme jako
$$\delta Q / T = f_{,T} \;\mathrm{d} T + f_{,V} \mathrm{d} V \, ,$$ tak funkce $f_{,T}$ a $f_{,V}$ splňují nutnou podmínku na existenci entropie, tedy že $$\frac{\partial f_{,T}(T, V)}{\partial V} = \frac{\partial f_{,V}(T, V)}{\partial T} $$
Janči se pokusil vymyslet jednodušší úlohu než posledně.
(3 body)5. Série 29. Ročníku - 3. egyptská brána
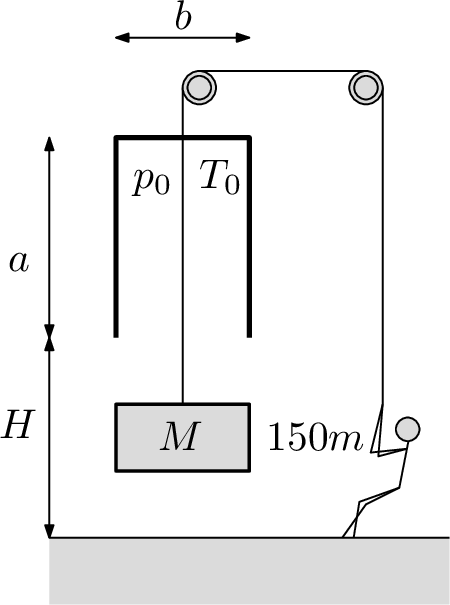
Ve starověkém Egyptu uměli vyrobit bránu, ale ještě neznali mříže, tak brány zavírali nilany (vápencovými kameny). Na obrázku vidíte $150$ otroků o hmotnosti $m=60\;\mathrm{kg}$, kteří právě velmi pomalu otevírají bránu zavřenou nilanem o hmotnosti $M=8\;\mathrm{t}$. Nilan přesně (vzduchotěsně) pasuje do konstrukce nad bránou ve tvaru kvádru, která má vnitřní rozměry $a=3\;\mathrm{m}$, $b=0,\! 5\;\mathrm{m}$ a $c=3\;\mathrm{m}$. Uvnitř konstrukce je na počátku tlak $p_{0}=100\; \mathrm{kPa}$ a teplota $T_{0}=300\; \mathrm{K}$ a je umístěna ve výšce $H=3\;\mathrm{m}$. Určete, jak vysoko jsou otroci schopni vlastní vahou nilan zdvihnout, jestliže se teplota vzduchu nemění.
Mirek rád předává otrockou práci jiným.
(6 bodů)5. Série 29. Ročníku - S. přirozeně proměnná
- Použijte vztah pro entropii ideálního plynu $S(U,V,N)$ z řešení třetí seriálové úlohy
$$S(U,V,N) = \frac{s}{2}n R \ln{\left( \frac{U V^{\kappa -1}}{\frac{s}{2}R n^{\kappa} } \right)} nR s_0$$
a vztah pro změnu entropie
$$\mathrm{d} S = \frac{1}{T}\mathrm{d} + U \frac{p}{T} \mathrm{d} V - \frac{\mu}{T} \mathrm{d} N$$
a vypočítejte chemický potenciál jako funkci $U$, $V$ a $N$. Upravte dále na funkci $T$, $p$ a $N$.
Pomůcka: Přečtěte si o derivacích a malých změnách v druhém díle seriálu. Nyní by už mělo být zřejmější, že koeficienty jako $1/T$ před $\mathrm{d}U$ spočítáte jako parciální derivaci $S(U,V,N)$ podle $U$. Nezapomeňte na užitečný vztah $\ln{(a/b)}=\ln{a}-\ln{b}$ a že $n=N/N_{A}$.
Bonus: Vyjádřete tímto způsobem i teplotu a tlak jako funkce $U$, $V$ a $N$. Eliminujte závislost tlaku na $U$, abyste dostali stavovou rovnici.
- Je chemický potenciál ideálního plynu kladný, nebo záporný ($s_{0}$ považujte za zanedbatelné)?
- Co se bude dít s plynem v pístu, pokud je plyn napojený na rezervoár s teplotou $T_{\mathrm{r}}?$ Píst se může volně pohybovat a z druhé strany na něj nic nepůsobí. Popište, co se bude dít, pokud dovolíme jen kvazistatické procesy. Kolik práce takto dokážeme extrahovat? Platí, že se takto minimalizuje volná energie?
Pomůcka: Na výpočet práce se vám může hodit vztah $$\int _{a}^{b} \frac{1}{x} \;\mathrm{d}x = \ln \frac{b}{a}.$$
- Entalpii jsme definovali jako $H=U+pV$, Gibbsovu energii jako $G=U-TS+pV$. Jaké jsou přirozené proměnné těchto potenciálů? Jaké termodynamické veličiny dostaneme derivacemi těchto potenciálů podle svých přirozených proměnných?
- Vypočítejte změnu grandkanonického potenciálu $\textrm{d}Ω$ z jeho definičního vztahu $Ω=F-μN$.
Janči se snažil představit si chemický potenciál.