Vyhledávání úloh podle oboru
Databáze úloh FYKOSu odjakživa
astrofyzika (85)biofyzika (18)chemie (24)elektrické pole (71)elektrický proud (76)gravitační pole (81)hydromechanika (146)jaderná fyzika (44)kmitání (57)kvantová fyzika (31)magnetické pole (43)matematika (89)mechanika hmotného bodu (298)mechanika plynů (87)mechanika tuhého tělesa (221)molekulová fyzika (72)geometrická optika (78)vlnová optika (65)ostatní (167)relativistická fyzika (37)statistická fyzika (21)termodynamika (155)vlnění (51)
mechanika hmotného bodu
3. Série 18. Ročníku - S. Lagrangeovy rovnice 1. druhu
Mějme hmotný bod zavěšený na nehmotném a nepružném vlákně.
- Zaveďte kartézskou souřadnicovou soustavu a v ní napište vazebnou podmínku pro hmotný bod.
- Napište Lagrangeovy rovnice 1. druhu pro hmotný bod z předchozí části. Ukažte, že jsou ekvivalentní s rovnicí matematického kyvadla $\frac{\rm{d}^{2} \varphi}{\rm{d}t^{2}} + \frac{g}{l} \sin \varphi = 0$, kde $\varphi$ je úhlová výchylka z rovnovážné polohy.
- Malé těleso je v klidu na vrcholu polokoule a začne klouzat dolů. Pomocí Lagrangeových rovnic 1. druhu určete, v jaké výšce se těleso odlepí od polokoule. ( Nápověda: Těleso se odlepí v okamžiku, kdy $\lambda = 0$.)
Úlohu zadali autoři seriálu Honza Prachař a Jarda Trnka.
2. Série 18. Ročníku - P. nečekaná překážka
Řidič automobilu jedoucí rychlostí $v$ ve vzdálenosti $l$ náhle spatří, že jeho vůz směřuje doprostřed betonové zdi šířky $2d$. Součinitel klidového tření mezi pneumatikami a vozovkou je $f$. Poraďte řidiči, co má dělat, aby se vyhnul srážce se zdí. Rozhodněte, pro jakou velikost rychlosti je to ještě možné.
Napadlo Pavla Augustinského při cestě autem.
2. Série 18. Ročníku - S. Newtonovy pohybové rovnice
Napište a řešte pohybové rovnice hmotného bodu v tíhovém poli Země. Souřadnicovou soustavu orientujte tak, že osy $x$ a $y$ jsou vodorovné a osa $z$ míří vzhůru. Počáteční poloha hmotného bodu je $r_{0} = (0,0,h)$, počáteční rychlost je $v_{0} =(v_{0}\cosα,0,v_{0}\sinα)$.
Muž s puškou sedí v křesle, které se otáčí kolem svislé osy s frekvencí $f = 1\, \jd{Hz}$. Spolu s křeslem se otáčí terč, který je k němu pevně upevněn. V jistém okamžiku muž vystřelí kulku rychlostí $v = 300\, \jd{km \cdot h^{-1}}$ směrem od osy otáčení přesně do středu terče. V jakém místě prorazí kulka terč? Řešte jak z pohledu neinerciální, tak z pohledu inerciální vztažné soustavy. Vzdálenost hlavně od středu terče je $l=3\, \jd{m}$, odpor vzduchu zanedbejte.
Vyjádřete závislost rychlosti hmotného bodu na poloze v gravitačním poli Slunce.
Zadal Honza Prachař.
1. Série 18. Ročníku - 1. ošklivé káčátko
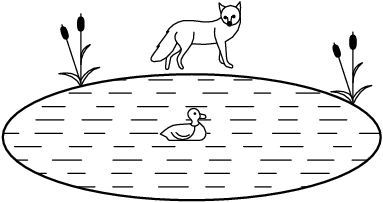
Opuštěné ošklivé kačátko zůstalo osamocené uprostřed kruhového rybníku. Chce se dostat za svými sourozenci a matkou kachnou, ale na břehu rybníka na něj číhá liška. Kačátko je ještě mladé, proto dokáže vzlétnout pouze z pevné země. Určete maximální poměr rychlostí běhu lišky a plavání kačátka, aby stihlo doplavat na břeh a z něj lišce uletět. Poraďte také kačátku, jakou strategii má zvolit.
Úlohu znala Lenka Zdeborová.
1. Série 18. Ročníku - 2. přistřižené kyvadlo
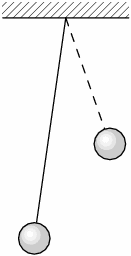
Malá hmotná kulička visí na konci nehmotného provázku a kmitá svojí vlastní frekvencí $f$ kolem rovnovážné polohy (viz obrázek). Jaká bude vlastní frekvence $f'$, pokud zkrátíme provázek na polovinu?
Úloha pochází z MFO v Kanadě, 1997.
1. Série 18. Ročníku - S. kinematika hmotného bodu
Poloha hmotného bodu v závislosti na čase v kartézské souřadnicové soustavě je popsána polohovým vektorem $r(t) =(R \cos\(\omega t\),R \sin\(\omega t\))$. Určete, jak závisí na čase vektory $v(t)$ a $a(t)$. Vypočítejte také tečnou, normálovou a binormálovou složku zrychlení.
- Kolo poloměru $R$ se valí bez prokluzování po přímé dráze rychlostí $v$. S kolem je pevně spojen bod ve vzdálenosti $r$ od středu. Určete jeho pohyb a rychlost jako funkce času v soustavě spojené se Zemí. Může být jeho rychlost v určitém okamžiku nulová?
Zadali autoři seriálu Honza Prachař a Jarda Trnka.
5. Série 17. Ročníku - 2. loď duchů
Loď duchů pluje proti proudu, jehož rychlost je $u$. Duchové jsou líní a slabí na přihazování uhlí do kotlů. Poraďte jim, jaká má být rychlost lodi $v$ vůči vodě, aby loď měla minimální spotřebu uhlí. Předpokládejte, že spotřeba paliva je úměrná vykonané práci na danou dráhu. Jak se výsledek změní, pokud místo lodního šroubu bude loď poháněna řetězem uloženým na dně řeky?
Navrhl Jirka Franta.
3. Série 17. Ročníku - 1. na oběžné dráze
Tři stejné družice obíhají po kružnici kolem malé planetky rychlostí $v$ tak, že jsou neustále ve vrcholech rovnostranného trojúhelníka. Určete jejich hmotnost, která není zanedbatelná vůči hmotnosti planetky.
Úlohu navrhl Honza Prachař.
3. Série 17. Ročníku - 4. kapitán Kork zasahuje
Vesmírná loď Escapeprise se vrací z prostoročasové bitvy s Odborgy. Během letu ale zjišťují, že nešťastnou náhodou směřují přímo do černé díry FAK-U0. Rozhodnou se pro úhybný manévr a kolmo na směr své rychlosti vypustí v jednom okamžiku všechno palivo. Vypočtěte vzdálenost, ve které Escapeprise kolem černé díry proletí. Jakou největší hmotnost může černá díra mít, nemá-li do ní Escapeprise spadnout? Jako bonus se zamyslete nad tím, zda kapitán Kork mohl úhybný manévr vymyslet chytřeji? Hmotnost samotné lodě je $M$, paliva $m$. Rychlost lodě ve velké vzdálenosti od černé díry je $V$ a směřuje do středu černé díry. Rychlost vypuštěného paliva je $v$ a úhybný manévr proběhl též velmi daleko od černé díry.
Vymyslel Jarda Trnka při sledování svého oblíbeného seriálu.
3. Série 17. Ročníku - P. jede, jede autíčko
Představte si autíčko, jehož motor má konstantní tažnou sílu $F$, pohybující se rychlostí $v$. Jeho výkon tedy je $P=Fv$. Avšak cyklista jedoucí konstantní rychlostí $u$ pozoruje výkon $P=F(v-u)$. Spotřeba benzínu, která odpovídá výkonu, je však stejná z pohledu cyklisty i stojícího chodce. Vysvětlete tento „paradox“. Odpor vzduchu neuvažujte.
Na klasický paradox v mechanice si vzpomněl Honza Prachař