Vyhledávání úloh podle oboru

Podle jedné z teorií vznikají hvězdy z oblaku mezihvězdné látky (kosmického prachu) smršťováním pod vlivem gravitačních sil. Určete dobu, za jakou se může zformovat hvězda z obrovského kulového oblaku kosmického prachu o hustotě $ρ=2\cdot 10^{–17}\;\textrm{kg}\cdot \textrm{m}^{–3}$. Můžete předpokládat, že se během smršťování částečky hmoty nepředbíhají a na začátku smršťování měly nulové rychlosti (oblak nijak nerotoval, nebyly v něm víry apod.). Zanedbejte také rozměry vzniknuvší hvězdy vůči počáteční velikosti oblaku.

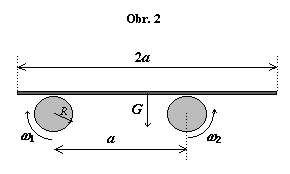
Dva stejné válce o poloměru $R$, jejichž osy jsou rovnoběžné a leží ve vodorovné rovině ve vzdálenosti $a$, rotují opačnými směry. Na tyto válce položíme vodorovně desku délky $2a$ o hmotnosti $m$ tak, že přečnívá vpravo více než vlevo (viz obr. 2). Mezi deskou a válcem působí tření s koeficientem $μ$. Co se bude dít s deskou,

• pokud jsou obvodové rychlosti stejně veliké,

• pokud je obvodová rychlost levého válce dvakrát větší než obvodová rychlost pravého?

Malý Ondra je na svůj věk velice zvídavý chlapec a místo hraní si s autíčky studuje takřka fyzikálně svět. Ve své stavebnici nalezl dřevěnou kouli a válec o stejném průměru i ze stejného materiálu a jal se dělat pokusy. Vhrnul kouli a válec (bez roztočení, viz obrázek) rychlostí $v_{0}$ po podlaze a sledoval, na jaké rychlosti $v$ se pohyb těles ustálí. Byl velice překvapen, když zjistil, že jedno z těles je rychlejší než druhé. Rozeberte teoreticky jeho „experimentální“ zjištění a určete konečné rychlosti těles. Uvažujte pouze smykové tření s koef. $μ$, valivé tření zanedbejte.

Chceme-li demonstrovat metodu řešení soustavy rovnic na našem skokanovi, budeme muset přidat další podmínku: dejme tomu, že první dopad na prkno se mu zdál příliš tvrdý; rozhodl se tedy rozkývat prkno natolik (změnit amplitudu kmitů), aby druhá srážka s prknem proběhla se zanedbatelnou vzájemnou rychlostí. Tedy jak hodnota Funkce, tak Derivace (uvedená v minulém díle) byla v okamžik srážky rovna nule. Vašim úkolem je najít potřebnou amplitudu $A_{n}$ a dobu druhého skoku $T_{n}$ (odráží se opět dole).

Dřevěný válec o poloměru $R$ a hmotnosti $m$ se valil po podlaze rychlostí $v$ do okamžiku, kdy se zarazil o zeď. O jaký úhel se ještě válec pootočí, než se úplně zastaví? Koeficient tření mezi válcem a stěnou resp. podlahou je $μ$.

Vašim milovaným strýčkem vám byl zadán úkol zjistit, zda jeho památeční rodinná lžička jest skutečně z ryzího hliníku. Vaše experimentální vybavení je však poněkud skromné: kromě uvedené lžíce dostanete k dispozici závaží o známé hmotnosti, dlouhé pravítko, provázek a dva hřebíky, které můžete zatlouct do zárubně dveří. Navíc zde ještě stojí kbelík plný vody. Navrhněte, výpočty podložte a hlavně proveďte měření, při kterém co nejpřesněji s pomocí jmenovaných pomůcek určíte hustotu materiálu lžičky. Uskutečněte dostatečné množství měření a na základě alespoň nějakých kalkulací také odhadněte věrohodnost vámi obdrženého výsledku.

Nápověda: Pokuste se srovnat hmotnost lžíce a závaží zavěšováním na provázek, který jste (s mírným průvisem) natáhli mezi zárubní dveří.

Liftboy v mrakodrapu si pověsil na stěnu svého výtahu přesné kyvadlové hodiny, aby viděl, kdy mu končí pracovní doba. Doba pohybu výtahu se zrychlením vzhůru a dolů je stejná. Zrychlení taktéž. Co si myslíte: bude mít chlapec pracovní dobu delší, kratší nebo stejnou?

Bicykl je neobvyklý tím, že jeho přední kolo je menší než zadní. Diskutujte, zda závisí výkon, který můžeme získat z alternátoru, na umístění na předním či zadním kole, případně na konkrétní poloze.

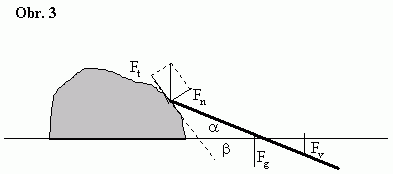
O kámen, vystupující do výšky $h$ nad hladinu vody, se jedním koncem opírá tenká deska délky $l$, která je částečně ponořena do vody. (viz obr. 3) Při jakém minimálním koeficientu tření mezi deskou a kamenem bude deska v rovnováze? Hustota dřeva je $ρ$, hustota vody $ρ_{0}$.

Položíte-li na nakloněnou rovinu dvě láhve, jednu prázdnou a jednu plnou, která z nich se bude kutálet rychleji (jsou to téměř válcové nádoby, osa symetrie kolmo na spádnici)? Pohyb na nakloněné rovině uvažujte bez tření a podkluzování. Přechází-li rovina v hrubší vodorovnou plochu, která z nádob po ní dojede dál? A uvedeme-li je na úpatí nakloněné roviny prudce do pohybu směrem vzhůru, která vyjede výše?