Vyhledávání úloh podle oboru
Databáze úloh FYKOSu odjakživa
astrofyzika (85)biofyzika (18)chemie (24)elektrické pole (71)elektrický proud (76)gravitační pole (81)hydromechanika (146)jaderná fyzika (44)kmitání (57)kvantová fyzika (31)magnetické pole (43)matematika (89)mechanika hmotného bodu (298)mechanika plynů (87)mechanika tuhého tělesa (221)molekulová fyzika (72)geometrická optika (78)vlnová optika (65)ostatní (167)relativistická fyzika (37)statistická fyzika (21)termodynamika (155)vlnění (51)
mechanika tuhého tělesa
5. Série 7. Ročníku - 3. tyč o stůl opřená
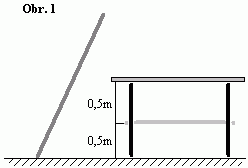
Část parket v obývacím pokoji je tak naleštěna, že po ní předměty kloužou se zanedbatelným třením. Pokoušíme se zde svisle postavit dvoumetrovou dřevěnou tyč, ale když už se nám to skoro podaří, dolní konec podklouzne a tíhová síla uvede tyč do pohybu. Padá volně tak, že její dolní konec klouže po podlaze. Jak musela minimálně být vzdálen deska stolu ve výšce 1 m, aby do ní tyč neuhodila (hrana stolu je kolmo na rovinu pádu tyče)?
Kdyby stůl stál naopak na druhé straně, jak by musel být daleko, aby tyč pod něj právě zajela (příčka mezi nohami stolu je ve výšce 0,5 m – viz obr. 1). Problém, zvláště jeho druhou část, je možné (a snadnější) řešit graficky, ať už s použitím počítače, nebo bez něj.
4. Série 7. Ročníku - 3. nešikovný cyklista
Roztržitý cyklista nezpozoroval, že v plné rychlosti najel do betonové zídky stojící kolmo k jeho dráze. Jakou nejvyšší rychlostí mohl jet, když nedošlo k deformaci ráfku.
4. Série 7. Ročníku - E. moment setrvačnosti smetáku
V této experimentální úloze je našim záměrem, abyste si všichni své navržené postupy také prakticky vyzkoušeli. Vymyslete a proveďte co nepřesnější metodu měření momentu setrvačnosti kuchyňského smetáku (s dlouhou násadou a příčkou na konci) vzhledem k ose rovnoběžné s násadou i ke kolmé na ni (procházející těžištěm). Pokuste se odhadnout přesnost vašeho měření.
3. Série 7. Ročníku - 1. hrabeme se v motoru
Při provozu zážehového motoru automobilu dochází k opotřebení vnitřních stěn válců. Zdůvodněte, v kterých místech válce bude jeho opotřebení největší. A jak je tomu u jiných pístových strojů, např. kompresoru?
1. Série 7. Ročníku - 2. gramofonová přenoska
Raménko s gramofonovou přenoskou je uchyceno v čepu a vyváženo závažím. Pokuste se zdůvodnit proč je celá soustava uspořádána tímto způsobem. Navrhněte velikost a umístění závaží, je-li hmotnost přenosky 15 g, tuhost jehly ve vertikálním směru 80 N\cdot m^{−1} a její vzdálenost od čepu je asi 200 mm, víte-li, že maximální přípustná síla, jíž může jehla tlačit na desku je 0,02 N. Hmotnost ramena přenosky zanedbejte.
1. Série 7. Ročníku - 4. korálek
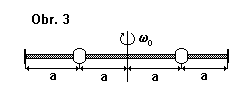
Na tyči zanedbatelné hmostnosti o celkové délce $4a$ jsou navlečeny ve vzdálenosti $a$ od osy otáčení dvě koule o hmotnosti $m$ (viz obr. 3). Na obou koncích tyče jsou umístěny dokonale pružné odrazné destičky. Tyč je roztočena na úhlovou rychlost $ω_{0}$, a poté jsou uvolněny obě koule. Za předpokladu, že se tyč nadále pohybuje volně a bez tření, určete:
- Po jaké trajektorii se budou pohybovat obě kuličky vzhledem k pozorovateli v inerciální soustavě.
- Jak se bude měnit úhlová rychlost soustavy $ω$ v závislosti na čase.
- Jak by se změnili výsledky předešlých úloh, kdybychom udržovali (např. pomocí motoru) úhlovou rychlost stále na hodnotě $ω_{0}?$
5. Série 2. Ročníku - 1. závažíčko na kouli
Na vrcholu koule poloměru $R$ leží závažíčko, které se v čase nula začne pohybovat. V jaké výšce a kdy se oddělí od povrchu koule?
3. Série 2. Ročníku - 2. klubíčko
Klubíčko s koncem připeněným k začátku nakoněné roviny se kutálí bez tření s podložkou a přitom se rozmotává. Co se při tom děje s energií klubíčka?
4. Série 1. Ročníku - 3. šílená Země
Jak by byl dlouhý den, kdyby se Země otáčela takovou rychlostí, že by se na rovníku kompenzovala odstředivá síla se silou gravitační? Jaké důsledky by tyto podmínky měly pro pohyb těles v různých zeměpisných šířkách (např. pro střelu pohybující se rychlostí $3000\; \textrm{m}\cdot \textrm{s}^{ -1}$ na dráze $6\; \textrm{km}$ ve směru poledníku)? Měla by Země tendenci se deformovat? Jak a proč? Uveďte další zajímavé důsledky.
2. Série 1. Ročníku - 4. pružiny
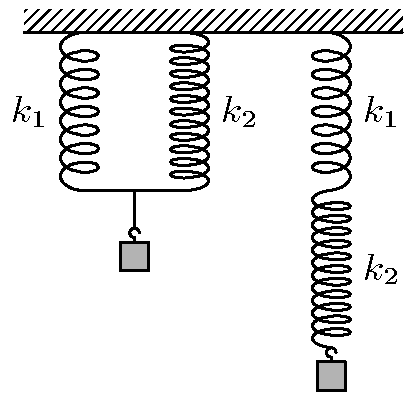
Model pružin
Pohrajme si s dvěma stejně dlouhými, ale různě tuhými pružinami. (Jejich tuhosti označíme $k_{1}$ a $k_{2}$.) Když je spojíme (viz obrázek), chovají se dohromady jako jediná pružina? Jaká je tuhost $k_{výsl}$ této „výsledné“ pružiny při spojení vedle sebe a jaká při spojení za sebou?