Vyhledávání úloh podle oboru
Databáze úloh FYKOSu odjakživa
astrofyzika (85)biofyzika (18)chemie (24)elektrické pole (71)elektrický proud (76)gravitační pole (81)hydromechanika (146)jaderná fyzika (44)kmitání (57)kvantová fyzika (31)magnetické pole (43)matematika (89)mechanika hmotného bodu (298)mechanika plynů (87)mechanika tuhého tělesa (221)molekulová fyzika (72)geometrická optika (78)vlnová optika (65)ostatní (167)relativistická fyzika (37)statistická fyzika (21)termodynamika (155)vlnění (51)
mechanika hmotného bodu
4. Série 9. Ročníku - E. ať žije sníh!
Je zima, blíži se jarní prázdniny, a jistě každý z vás se chystá do hor lyžovat, čehož jsme se rozhodli zneužít, a tak vám zadáváme následující úlohu: Změřte koeficient tření lyžaře na sněhu.
K dispozici máte cokoliv, zejména tedy toho lyžaře, lyže (kdo provede měření pro porovnaní zvlášť na běžkách a zvlášť na sjezdovkách, bude mít plus), sjezdovku (fyzikálně řečeno nakloněnou rovinu), měřič času (normálně řečeno stopky) a jiné věci, co vás napadnou a co byste mohli upotřebit. Pokud byste se chtěli vymlouvat, že letos již lyžovat nebudete, není problém tuto úlohu změřit i na rovině. Je jisté, že i ve vaší vesnici (městě, nebo v čem jiném bydlíte) bude alespoň jeden den sníh.
Pozn.: Nezapomeňte, že navoskované lyže na sněhu je krásný případ systému, kde koeficient tření závisí na rychlosti a možná i na povrchu styčné plochy, což můžete ověřit jízdou po jedné lyži. Bohužel však vzhledem k odporu vzduchu a dalším ručivým vlivům budou asi tyto efekty špatně měřitelné (ve vyšší rychlosti sice trochu klesne koeficient tření, zato značně vzroste odpor vzduchu).
3. Série 9. Ročníku - 1. vyhlodaný hranol
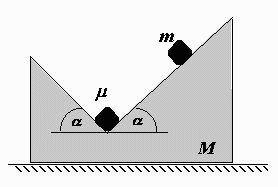
Na vodorovné rovině je položen vyhlodaný hranol o hmotnosti $M$ (viz obrázek), který se po ní může bez tření pohybovat. V nejnižším místě leží krychlička o hmotnosti $μ$. Na nakloněné části hranolu leží krychlička o hmotnosti $m$. I malé krychličky se mohou pohybovat po vyhlodaném hranolu bez tření. Jaká musí být splněna podmínka mezi hmotnostmi $M$, $m$, $μ$ a úhlem α, aby se po uvolnění krychličky $m$ krychlička $μ$ začala vůči hranolu $M$ pohybovat?
3. Série 9. Ročníku - 3. Pinocciova čepička
Papa Karlo zhotovil pro Pinoccia čepičku z tenkého plechu ve tvaru kužele o výšce $20\;\textrm{cm}$ a s vrcholovým úhlem $60^\circ$. Bude ale takováto ozdoba držet na jeho hlavě, která má tvar koule o poloměru $15\;\textrm{cm}$ a je dokonale hladká?
3. Série 9. Ročníku - P. vodní kyvadlo
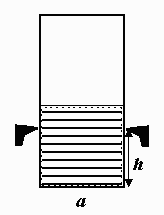
Mějme nádobu tvaru kvádru zanedbatelné hmotnosti o čtvercové podstavě strany $a$ a výšce $2a$. V této nádobě se nachází krychlové vodní těleso. V jaké maximální výšce $h$ ode dna můžeme naši nádobu zavěsit, aby se po zmrznutí vody převrátila? (Viz obrázek 2, který znázorňuje řez nádoby vertikální rovinou procházející těžištěm.) Uvažujte dva případy:
- nádoba je dokonale tuhá a voda zamrzá ode dna,
- voda si během zamrzání uchovává stále svůj krychlový tvar, nádoba je tedy dostatečně pružná. Přitom podél stěn led klouže, tedy výška závěsu nad podstavou zůstává konstantní.
2. Série 9. Ročníku - 1. Nezbedkova Nezbedka
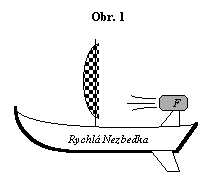
Na obrázku 1 plove loďka. Její majitel, známý vynálezce a kutil Nezbeda, vyřešil problém bezvětrného počasí následujícím způsobem: na záď lodi připevnil výkonný fén značky Fukar a nasměroval jej vpřed přímo na malou lodní plachtu. Na vás teď je, abyste usoudili, za jakých podmínek se loďka rozjede vpřed či vzad. Můžete se také zamyslet nad tím, jaké zlepšovací návrhy byste Nezbedovi poradili, aby jeho pohon pracoval za bezvětří co nejefektivněji.
2. Série 9. Ročníku - 3. válcovací stolice
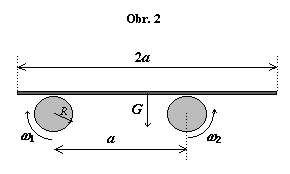
Dva stejné válce o poloměru $R$, jejichž osy jsou rovnoběžné a leží ve vodorovné rovině ve vzdálenosti $a$, rotují opačnými směry. Na tyto válce položíme vodorovně desku délky $2a$ o hmotnosti $m$ tak, že přečnívá vpravo více než vlevo (viz obr. 2). Mezi deskou a válcem působí tření s koeficientem $μ$. Co se bude dít s deskou,
- pokud jsou obvodové rychlosti stejně veliké,
- pokud je obvodová rychlost levého válce dvakrát větší než obvodová rychlost pravého?
1. Série 9. Ročníku - P. lokomotivy
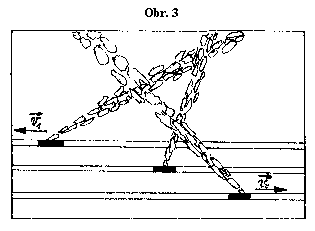
Na obrázku je letecký snímek parních lokomotiv s oblaky dýmu, které se pohybují rovnoměrně po přímých rovnoběžných kolejích. Rychlost první parní lokomotivy je $v_{1}=50\;\mathrm{km} \cdot \mathrm{h}^{-1}$, rychlost třetí $v_{3}=70\;\mathrm{km} \cdot \mathrm{h}^{-1}$. Směry rychlostí jsou vyznačeny na obrázku. Jaká je rychlost $v_{2}$ druhé lokomotivy?
6. Série 8. Ročníku - 1. Jupiter a kometa
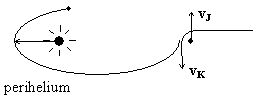
Trajektorie planety
Kometární rodina Jupiteru vzniká následujícím způsobem (viz. obrázek). Kometa přilétá k Jupiteru z velké vzdálenosti s téměř nulovou počáteční rychlostí. Po opuštění Jupiterova gravitačního pole (přesně sféry gravitačního vlivu Jupitera), má její rychlost (vzhledem ke Slunci) přesně opačný směr než rychlost Jupitera. Poté se pohybuje opět v gravitačním poli Slunce. V jaké vzdálenosti od něj se bude nacházet perihelium dráhy komety a jaká je její oběžná doba (jaká je velikost velké poloosy dráhy komety)? Uvažujte, že Jupiter obíhá kolem Slunce po kružnici o poloměru $R=5,2\;\mathrm{AU}$.
5. Série 8. Ročníku - 1. vesmírná katastrofa
Tři planetky o stejné hmotnosti $M=10^{26}\; \textrm{g}$ jsou umístěny ve vrcholech rovnostranného trojúhelníka o straně $l=100\; \textrm{Gm}$ [gigametry]. Nemajíce počáteční rychlosti nezbývá jim než padat vstříc jisté záhubě. Určete, za jak dlouho se srazí (rozměry planetek zanedbejte).
5. Série 8. Ročníku - P. co ten skokan pořád chce
Chceme-li demonstrovat metodu řešení soustavy rovnic na našem skokanovi, budeme muset přidat další podmínku: dejme tomu, že první dopad na prkno se mu zdál příliš tvrdý; rozhodl se tedy rozkývat prkno natolik (změnit amplitudu kmitů), aby druhá srážka s prknem proběhla se zanedbatelnou vzájemnou rychlostí. Tedy jak hodnota Funkce, tak Derivace (uvedená v minulém díle) byla v okamžik srážky rovna nule. Vašim úkolem je najít potřebnou amplitudu $A_{n}$ a dobu druhého skoku $T_{n}$ (odráží se opět dole).