Vyhledávání úloh podle oboru
Databáze úloh FYKOSu odjakživa
astrofyzika (85)biofyzika (18)chemie (24)elektrické pole (71)elektrický proud (76)gravitační pole (81)hydromechanika (146)jaderná fyzika (44)kmitání (57)kvantová fyzika (31)magnetické pole (43)matematika (89)mechanika hmotného bodu (298)mechanika plynů (87)mechanika tuhého tělesa (221)molekulová fyzika (72)geometrická optika (78)vlnová optika (65)ostatní (167)relativistická fyzika (37)statistická fyzika (21)termodynamika (155)vlnění (51)
gravitační pole
(9 bodů)4. Série 31. Ročníku - P. Voyager II a Voyager I žijí!
Máme nějaký satelit, který chceme vypustit ven ze Sluneční soustavy. Vypouštíme ho z oběžné dráhy Země tak, že po nějakých korekcích dráhy získá rychlost, která je vyšší než úniková rychlost ze Sluneční soustavy. Jaká je pravděpodobnost, že dojde ke kolizi sondy s nějakým kosmickým materiálem s průměrem větším než $d = 1 \mathrm{m}$ před opuštěním Sluneční soustavy?
Karel si říkal, proč ta NASA tuhle možnost ani neuvažuje…
(3 body)3. Série 31. Ročníku - 2. zrychleníčko, zrychlení
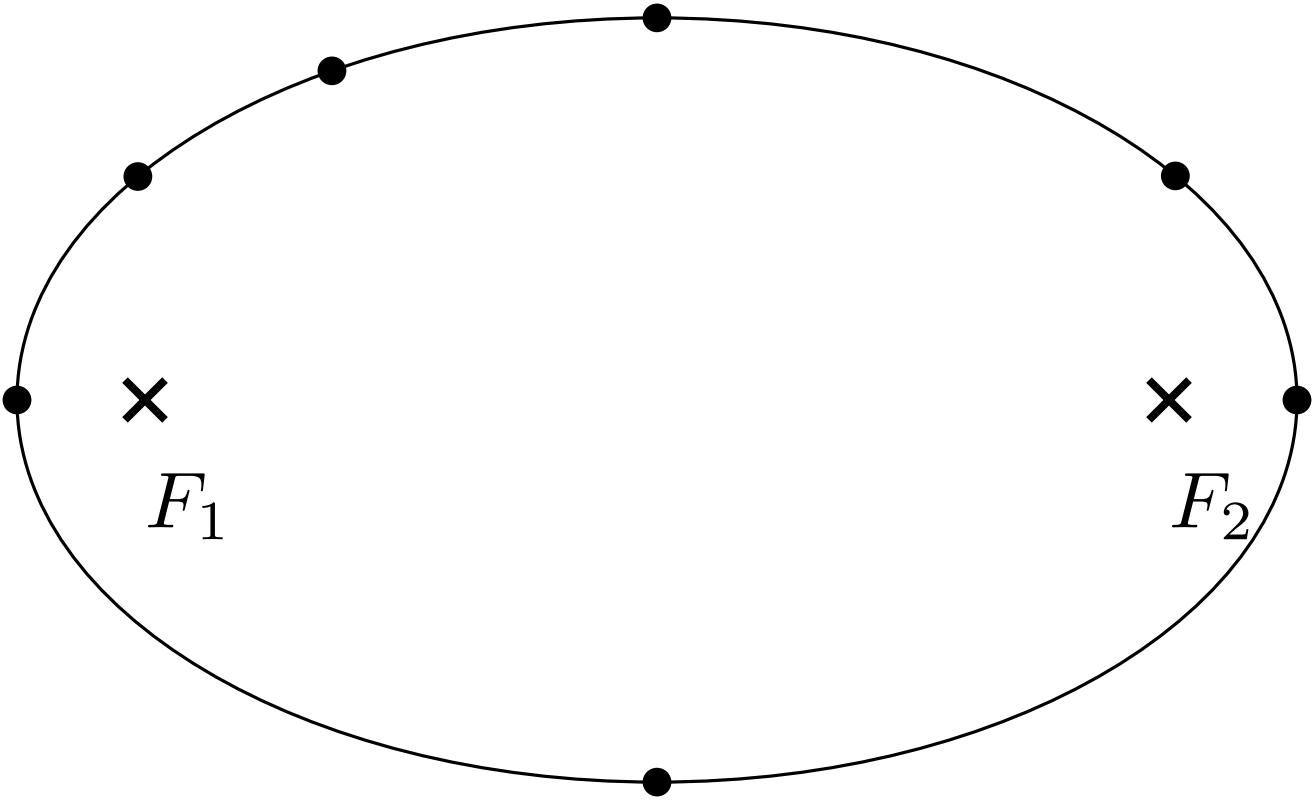
Náčrt elipsy
Na obrázku vidíte náčrt elipsy s ohnisky $F_1$ a $F_2$ a několika vyznačenými body na ní. Uvažujte, že elipsa znázorňuje trajektorii nějakého hmotného bodu. Znázorněte do obrázku zrychlení, která působí na hmotný bod v jednotlivých vyznačených bodech dráhy pro dvě situace (jde o směry a vzájemné poměry zrychlení (které je větší/menší) v různých bodech v rámci jednoho náčrtu).
- V ohnisku $F_1$ je umístěno hmotné těleso, kolem kterého hmotný bod obíhá. Uvažujeme, že platí 2. Keplerův zákon.
- Těleso má konstantní velikost rychlosti, pouze se pohybuje po elipse.
Karel na konferenci slyšel, že s takovými úlohami mají problémy i vysokoškoláci.
(3 body)6. Série 30. Ročníku - 2. upadlo
Z jaké výšky nad povrchem neutronové hvězdy bychom museli „upustit“ předmět, aby dopadl na její povrch v rychlosti $0,\! 1\; c$ (0,1 rychlosti světla). Naše neutronová hvězda má hmotnost 1,5násobek hmotnosti Slunce a průměr $d=10\;\mathrm{km}$. Zanedbejte atmosféru neutronové hvězdy a její rotaci. Zanedbejte relativistické korekce. Srovnejte ale jakého výsledku byste dosáhli, pokud by pád probíhal v homogenním gravitačním poli (které má intenzitu stejnou jako na povrchu planety) s tím, kdy pád probíhá v radiálním gravitačním poli.
Bonus: Uvažujte korekci na speciální teorii relativity v případě pádu v homogenním poli.
Karel přemýšlel, zas a znovu, nad neutronovými hvězdami.
(3 body)5. Série 30. Ročníku - 1. vesmírný sněhulák
Jakou silou bude přidržována hlava našeho sněhuláka, který si volně poletuje ve vesmíru? Máme sněhuláka tvořeného pouze homogenními koulemi o hustotě $ρ$, jejichž středy leží na jedné přímce a koule se dotýkají, jsou umístěné v pořadí od největší po nejmenší a s tím, že nejmenší koule (hlava) má poloměr $r$ a každá další má dvojnásobný poloměr, co ta předchozí. Ve vesmíru je pouze náš sněhulák a nijak nerotuje.
Bonus: Zobecněte úlohu pro počet koulí $N \geq 3$. Bude se síla blížit nějaké konečné hodnotě pro $n→∞$, nebo půjde k nekonečnu?
Karel vymýšlel úlohu na Fyziklání a pak si řekl, že by ten výsledek nechtěl kontrolovat.
(12 bodů)1. Série 30. Ročníku - E. Pechschnitte
Padá krajíc namazanou stranou dolů? Zkoumejte experimentálně tento Murphyho zákon s důrazem na statistiku! Záleží na rozměrech krajíce, složení a typu vrstvy? K experimentálním výsledkům hledejte teoretická zdůvodnění. Pro vaše měření použijte toastový chléb.
Terka má stůl ve špatné výšce.
(8 bodů)1. Série 30. Ročníku - P. nebe padá na hlavu
Už jste se někdy zamysleli nad tím, proč mraky nespadnou na zem, když jsou z vody, která má přece výrazně větší hustotu než vzduch? Dešťové kapky dopadnou na zem v řádech minut, tak proč ne i mraky? Zkuste tuto skutečnost fyzikálně objasnit. Veškerá svá tvrzení podložte výpočtem.
Mirek se zadíval na nebe a dostal strach.
(8 bodů)6. Série 29. Ročníku - E. zákeřný restituční koeficient
Pokud pustíte hopík či nějaký jiný míček na vhodný povrch, pak se začne odrážet. Při každém odrazu se disipuje (ztrácí do tepla, zvuku atd.) kinetická energie míčku a proto nevyskočí do takové výše, co původně. Definujme koeficient restituce jako poměr kinetických energií míčku po dopadu ku kinetické energii před dopadem. Závisí koeficient restituce na výšce, ze které míček dopadal? Vyberte si jeden vhodný míček a jeden vhodný povrch, na kterém proměřte závislost koeficientu restituce na výšce, ze které míček dopadl. Experiment náležitě popište a proveďte dostatečný počet měření. Nezapomeňte na vliv odporu vzduchu.
Karel zavzpomínal, jak ho jednou zamrzelo, že u ping-pongového míčku má velký vliv odpor vzduchu.
(6 bodů)6. Série 29. Ročníku - P. i-jablko
Vymyslete co nejvíce způsobů, jak sestrojit zařízení, které pozná, jakým směrem je natočeno vůči směru tíhového zrychlení a tuto informaci nějakým způsobem převede na elektrický signál. (Zařízení na způsob akcelerometru v chytrých telefonech.)
Napadlo Terku, když už se jí nechtěla učit analýza.
(3 body)2. Série 29. Ročníku - 3. fatální upuštění
Z rakety obíhající po kružnici ve výšce $h=2000\;\mathrm{km}$ nad Zemí hodíme směrem k Zemi nebohý šroubovák rychlostí $v=5\;\mathrm{km}\cdot \textrm{h}^{-1}$ vůči lodi. Za jak dlouho dopadne?
Karel nemá rád šroubováky.
(8 bodů)1. Série 29. Ročníku - E. malé gé
Změřte místní tíhové zrychlení alespoň dvěma odlišnými metodami. Tyto metody následně zevrubně porovnejte.
Viktor slyšel námitku řešitelů, že je nebaví se pořád čvachtat ve vodě.