Vyhledávání úloh podle oboru

• Jakubova snídaně

Jakub jí ke snídani cereální kuličky o hustotě $ρ$, které si sype do misky ve tvaru komolého kužele (horní podstava má poloměr $R$, spodní $r$ a výška je $l)$, ve kterém má do výšky $h$ nalité mléko. Kolik nejvíce kuliček může do misky nasypat? Víte, že kuličky v plné velké krabici zabírají přibližně objemový podíl $κ$.

• magnetický monopol

Máme velkou plechovou desku, kterou zmagnetujeme tak, že na její horní ploše bude severní magnetický pól (a na dolní ploše ten jižní). Vylisujeme z ní dvě stejné polokoule. Na vnitřní straně obou polokoulí je teď jižní a na vnější severní pól. Polokoule k sobě přiblížíme tak, že vyrobíme celou kouli. Ta má nyní venku pouze severní pól, takže se chová jako magnetický monopól. A nebo ne? Co nám vytvoření takovéto koule zabrání?

Ve starém gauči našel Lukáš pružinu o tuhosti $k$, poloměru závitu $r$, délky $l$ a počtem závitů $n$. Protože se nudil, připojil ji ke stabilnímu zdroji elektrického proudu $I$. Jak se změnila její tuhost?

Odkud bere magnet energii na zvedání věcí, když magnetická síla nemůže konat práci? Lorentzův vzorec $\vect{F} = q ( \vect{v}\times \vect{B})$ říká, že magnetická síla je kolmá na rychlost pohybujícího se náboje, a tedy pouze mění jeho směr hybnosti.

Cela, ve které je pterodaktyl vězněn, je uzamčena pomocí magnetického zámku. Americké tajné služby vlastní prototyp tohoto zámku a kousek z jeho magnetu vám posíláme v obálce se sérií. K otevření zámku bez klíče je nutné znát, jak závisí síla mezi dvěma magnety na jejich vzdálenosti. Změřte co nejpřesněji tuto závislost!

Návod: Mezi oba magnety postupně vkládejte tenké listy papíru a měřte sílu nutnou na odtržení magnetků od sebe.

Dva stejné náboje umístíme na oba konce tuhé nevodivé tyčky. Jaký výkon budeme potřebovat na otáčení tyčky konstantní úhlovou rychlostí kolem osy procházející středem tyčky. Tření zanedbejte.

Na hřídeli elektromotoru je navinuta nit, na konci které je zavěšeno závaží o hmotnosti $m$. Pokud motor připojíme na ideální zdroj napětí $U$, závaží pojede vzhůru rychlostí $v_{1}$. Jakou rychlostí bude závaží klesat, pokud zdroj odpojíme a vstup elektromotoru zkratujeme? Mechanické tření neuvažujte.

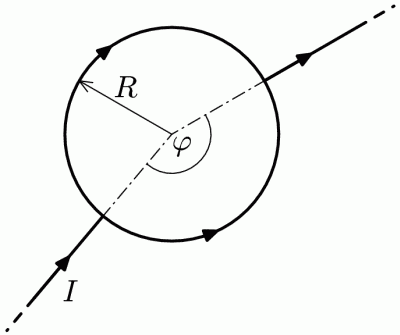
Představte si kruhovou smyčku tvořenou drátem. Radiálními vodiči přivádíme a odvádíme elektrický proud (viz obrázek). Jaké bude magnetické pole uprostřed smyčky? Poloměr smyčky je $R$, úhel mezi radiálními přívodními dráty $φ$ a proud v drátu $I$.

• Uvažujte potenciál elektrického pole, pro který platí

φ($\textbf{r})=\textbf{r}\cdot \textbf{A}\,,$

kde $\textbf{A}$ je konstantní vektor. Spočtěte vektor elektrické indukce, když víte, že $\textbf{E}=–\rm{grad}φ\,.$

• Spočtěte vektor magnetické indukce $\textbf{B}$, pokud pro vektorový potenciál platí

$\textbf{A}=(\textbf{r}×\textbf{G})/r\,,$

kde $\textbf{G}$ je konstantní vektor. Magnetickou indukci můžeme spočítat ze znalosti vektorového potenciálu pomocí vztahu $\textbf{B}=\rm{rot}\textbf{A}\,.$

• Určete, co je výsledkem působení Laplaceova operátoru na polohový vektor $\textbf{r}$. Laplaceův operátor působící na vektor definujeme podle vztahu

$Δ\textbf{A} = \rm{grad}\, \rm{div} \textbf{A} – \rm{rot}\, \rm{rot} \textbf{A}\,.$

Kovová palička může kmitat okolo koncového bodu. Její druhý konec se stále dotýká kovového oblouku. Bod závěsu je přes kondenzátor kapacity $C$ zapojený na střed kovového oblouku (t.j. nejnižší bod, ve kterém se nachází dolní konec paličky). Celé kyvadélko se nachází v homogenním magnetickém poli indukce $B$, které je kolmé na rovinu kmitů. Jaká je doba kmitu kyvadla, pokud hmotnost paličky je $m$ a tření a odpor drátu zanedbáme. Počáteční výchylku kyvadla $\alpha_{0}$ uvažujeme menší než $5\, \jd{^{\circ}}$.

• Určete velikost a směr magnetické indukce kruhového závitu o poloměru $a$. Uvažujte bod na ose závitu ve vzdálenosti $z$ od středu kruhové smyčky.
• Určete velikost a směr vektorů magnetické indukce $\textbf{B}$ a vektorového potenciálu $\textbf{A}$ ve vzdálenosti $a$ od přímého vodiče délky $l$, pokud jím prochází proud $I$.