Vyhledávání úloh podle oboru

Dělník si na stavbu mrakodrapu přinesl vak se skleněnkami, aby se s nimi mohl pochlubit svým kolegům. A co se nestane – vak se vysype a kuličky padají skrze lešení směrem k zemi. Lešení se skládá z jednotlivých poschodí o výšce $h$. Podlaha každého poschodí se skládá ze stejných mříží, ve kterých díry zaujímají $k  \%$ z celkové plochy mříže. Uvažujme zjednodušený model propadávání kuliček lešením, kdy, pokud kulička spadne na díru v lešení, tak projde bez ovlivnění, a pokud spadne na pevnou část mříže, tak se její rychlost sníží na $0$ a ihned začne dále padat (tj. velikost kuliček je zanedbatelná vůči velikosti děr v lešení, kuličky se od lešení nijak neodráží a po dopadu na pevnou část mříže se ihned skutálí do díry a dále začínají padat). Nakonec neuvažujme ani potenciální srážky kuliček mezi sebou. Předpokládejte, že kuličky se z tašky sypou s konstantním hmotnostním průtokem $Q$. Jakou silou budou kuličky působit na každé patro lešení, až se situace ustálí?

Jaké vlastnosti má 118. prvek periodické soustavy prvků? Respektive jaké by asi měl, kdyby byl stabilní? Diskutujte alespoň tři fyzikální vlastnosti.

1. Vykreslete závislost chyby na velikosti kroku pro metodu odvozenou pomocí Richardsonovy extrapolace v textu seriálu. Jaký je optimální krok a minimální chyba? Porovnejte s centrovanou a dopřednou diferencí. Jako derivovanou funkci použijte $\exp(\sin(x))$ v bodě $x=1$.
   Bonus: Vypočtěte pro tuto metodu teoretickou velikost optimálního kroku pomocí odhadu chyb.
2. Na webu se nachází soubor s experimentálně zjištěnými $t$, $x$ a $y$ souřadnicemi poloh hmotného bodu. Pomocí numerické derivace nalezněte časovou závislost složek rychlosti a zrychlení a vyneste obě závislosti do grafu. Jaký fyzikální děj bod nejspíše konal? Numerickou metodu si zvolte sami, svoji volbu ale odůvodněte.
   Bonus: Existuje v tomto případě přesnější varianta získání rychlosti a zrychlení, než přímočará aplikace numerické derivace?
3. Máme zadán integrál $\int _0^{\pi } \sin ^2 x\,\d x$.
   1. Nalezněte hodnotu integrálu z geometrické úvahy za pomoci Pythagorovy věty.
   2. Nalezněte hodnotu integrálu pomocí Monte Carlo simulace. Určete směrodatnou odchylku výsledku.
      Bonus: Vyřešte Buffonovu úlohu ze seriálu (odhad hodnoty čísla $\pi$) pomocí MC simulace.
4. Nalezněte vztah pro výpočet objemu šestidimenzinální koule pomocí metody Monte Carlo.
   Nápověda: Pythagorovu větu lze využít k měření vzdáleností i ve vyšších dimenzích.

1. Upravte výraz $\sqrt {x+1}-\sqrt {x}$ tak, aby nebyl náchylný k problémům cancellation, ordering a smearing. Ke kterým z těchto problémů byl původně náchylný a proč? Jaký je rozdíl ve výsledku původního a opraveného výrazu, pokud jej vyčíslíme v double precision pro $x=1{,}0 \cdot 10^{10}$?
2. Popište funkci následujícího kódu. Jaký je rozdíl mezi funkcemi a() a b()? Pro jaké hodnoty x je lze použít? Nebojte se kód spustit a hrát si s hodnotou proměnné x. Určete také asymptotickou časovou složitost programu v závislosti na proměnné x.

   def a(n):
     if n == 0:
       return 1
     else:
       return n*a(n-1)
   def b(n):
     if n == 0:
       return 1.0
     else:
       return n*b(n-1)
   x=10
   print("{} {} {}".format(x, a(x), b(x)))

3. Označme $o_k$ a $O_k$ obvod vepsaného a opsaného pravidelného $k$-úhelníku ke kružnici. Pak pro ně platí rekurentní vztahy \[\begin{equation*} O_{2k}=\frac {2o_k O_k}{o_k + O_k} ,\; o_{2k}=\sqrt {o_k O_{2k}} . \end {equation*}\] Napište program, který pomocí těchto vztahů vypočítá hodnotu $\pi $, začněte přitom s opsaným a vepsaným čtvercem. S jakou přesností dokážete $\pi $ takto aproximovat? Obdobu tohoto postupu původně navrhl a použil Archimedes.
4. Lukáš a Mirek hrají hru. Házejí férovou mincí a když padne orel, dá Mirek Lukášovi jedno Fykosí tričko, když padne panna, dá jedno tričko Lukáš Mirkovi. Oba dohromady mají $t$ triček, z toho $l$ patří Lukášovi a $m$ Mirkovi. Pokud jednomu z hráčů dojdou trička, hra končí.
   1. Nechť $m = 3$ a Lukášova zásoba triček je nekonečná. Určete nejpravděpodobnější dobu trvání hry, tedy počet hodů mincí, po nichž hra skončí (protože Mirkovi dojdou trička).
   2. Nechť $m = 10$, $l = 20$. Proveďte simulaci pomocí generátoru pseudonáhodných čísel a nalezněte pravděpodobnost, že Mirek vyhraje všechna Lukášova trička. Celou hru nechejte proběhnout alespoň 100krát (čím více opakování, tím lépe).
   3. Jak se změní výsledek předchozí úlohy, jestliže Mirek minci „vylepší“ a panna nyní padá s pravděpodobností $5/9$?
      Bonus: Vypočtěte pravděpodobnosti analyticky a porovnejte výsledek se simulací.
5. Mějme lineární kongruenční generátor s parametry $a = 65539$, $m = 2^{31}$, $c = 0$.
   1. Vygenerujte alespoň $1 000$ čísel a spočtěte jejich střední hodnotu a rozptyl. Porovnejte se střední hodnotou a rozptylem rovnoměrného rozdělení na stejném intervalu.
   2. Nalezněte vztah, který vyjádří číslo v generované sekvenci jako lineární kombinaci čísel na dvou předchozích pozicích, tj. nalezněte koeficienty $A$, $B$ v rekurentním vztahu $x_{k+2} = Ax_{k+1} + Bx_k$. Pokud budeme považovat každá tři po sobě následující čísla za souřadnice bodu ve trojrozměrném prostoru, jak rekurentní vztah ovlivní prostorové rozložení těchto bodů?
      Bonus: Vygenerujte sekvenci alespoň $10 000$ čísel a vykreslete 3D bodový graf, který ilustruje význam uvedeného rekurentního vztahu.

Elza ráda cestuje vlakem. Při tom si všimla, že ihned po zastavení vlak mírně cukne dozadu. Elza nemá tušení, proč tomu tak je, pomozte jí to tedy objasnit. Uvažujte vlak s lokomotivou (hmotnost $m_r = \mathrm{82 t}$) a čtrnácti vagóny (hmotnost každého z nich je $m_v = \mathrm{48 t}$). Lokomotiva má brzdící váhu $p_r = \mathrm{113 t}$ a každý z vagónů má $p_v = \mathrm{99 t}$.$^1$ Dále uvažujme, že po zabrzdění se brzdící impulz šíří s konstantní rychlostí od lokomotivy na konec vlaku, přičemž poslední vagón začne brzdit za čas $\Delta t = \mathrm{12 s}$ po mašině.

Pro úplnost uvažujme, že spřáhla vozů jsou z části volná a umožňují pohyb. Sílu, kterou působí, můžeme v závislosti na výchylce $x$ popsat jako $x < 0 \Rightarrow F = -x k  ,$

$x = 0 \Rightarrow F = 0  ,$

$x > 0 \Rightarrow F = A \mathrm{sgn} \(x - x_v\)  ,$

kde kladný směr je tehdy, pokud se vozy od sebe vzdalují. Dále $k$ je tuhost nárazníku, $x_v$ je nezáporná konstanta a $A$ je tuhost spřáhla, přičemž $A \gg k$.

1. Analyticky vyšetřete průběh brzdění vlaku.
2. Najděte vlastní frekvenci kmitů pro $n$-tý vagón.
3. Najděte parametry $k$, $A$ a $x_v$ tak, aby kmitání vozů bylo vzhledem k brzdění kriticky tlumené.
4. Splňuje tento model to, co Elza pozorovala? Udělejte Elze radost a najděte lepší model chování vlaku.
5. Numericky řešte tento nový model.

Bonus: Řešte případ, ve kterém bude jeden z vozů vypojený, tedy nebude brzdit.

1.) Brzdící váha označuje poměrnou schopnost vozidla brzdit. Je to absolutní jednotka a můžeme jí lineárně přeškálovat na brzdící sílu.

• Zkuste vlastními slovy popsat, k čemu a jak se používá nelineární regrese (postačí vlastními slovy popsat následující: model nelineární regrese, způsob odhadu regresních koeficientů, vyjádření nejistot odhadů regresních koeficientů a hodnot prokládané funkce, statistické testy hodnot regresních koeficientů, identifikovatelnost parametrů a způsob volby prokládané funkce). Není potřeba uvádět přesná matematická odvození, stačí požadované pojmy a vlastnosti stručně popsat.
• V přiloženém datovém souboru regrese1.csv naleznete dvojice hodnot $(x_{i},y_{i})$. Těmito daty chceme proložit teoretickou funkční závislost, kterou je v tomto případě sinusoida, tedy funkce tvaru

$$f(x)=a + b \cdot \sin{(cx + d)}\, .$$ Vykreslete graf naměřených hodnot a proložené funkce a stručně ho okomentujte (takovýto graf musí mít všechny náležitosti). Není potřeba dělat regresní diagnostiku.
Nápověda: Dejte si pozor na identifikovatelnost parametrů v tomto modelu a vhodné omezující podmínky na parametr $c$.

• V přiloženém datovém souboru regrese2.csv naleznete dvojice hodnot $(x_{i},y_{i})$. Těmito daty chceme proložit teoretickou funkční závislost, kterou je v tomto případě exponenciála, tedy funkce tvaru

$$f(x)=a + \mathrm{e}^{bx + c}\, .$$ Určete hodnoty odhadů všech regresních koeficientů včetně nejistot měření.
Nápověda: Grafickou metodou ověřte předpoklad homoskedasticity a v případě potřeby pro určení nejistot měření regresních koeficientů použijte Whiteův (sendvičový) odhad kovarianční matice.

• V přiloženém datovém souboru regrese3.csv naleznete dvojice hodnot $(x_{i},y_{i})$. Těmito daty chceme proložit teoretickou funkční závislost, kterou je v tomto případě hyperbola, tedy funkce tvaru

$$f(x)=a + \frac{1}{bx + c}\, .$$ Vykreslete graf naměřených dat v podobě průměrů a chybových úseček a proložené funkce a stručně ho okomentujte (takovýto graf musí mít všechny náležitosti). Proveďte regresní diagnostiku.

Bonus: V přiloženém datovém souboru regrese4.csv naleznete dvojice hodnot $(x_{i},y_{i})$. Těmito daty chceme proložit teoretickou závislost, která je ovšem příliš složitá na analytické vyjádření. Proložte těmito daty regresní spliny (s vhodně zvolenými uzly a vhodně zvoleným stupněm). Pro práci s daty použijte výpočetní prostředí R. Pro vyřešení těchto úkolů postačí drobně upravit přiložený skript, ve kterém je pomocí komentářů v kódu vysvětlena potřebná syntaxe jazyka R.

• skript v kódování UTF-8
• skript v kódování CP-1250
• regrese1.csv
• regrese2.csv
• regrese3.csv
• regrese4.csv
• ukazka1.csv
• ukazka2.csv
• ukazka3.csv

• Zkuste vlastními slovy popsat, k čemu a jak se používá lineární regrese (postačí vlastními slovy popsat následující: dva hlavní případy aplikace lineární regrese, používaný model, předpoklady modelu, postup volby prokládané funkce, způsob vyjádření nejistot měření, základní grafické metody regresní diagnostiky). Není potřeba uvádět přesná matematická odvození, stačí požadované pojmy a vlastnosti stručně popsat.
• V přiloženém datovém souboru linreg1.csv naleznete výsledky určitého fyzikálního experimentu, ve kterém jsme měřili dvojice dat $(x_{i},y_{i})$. Naměřenými daty chceme proložit teoretickou funkci, kterou je v tomto případě parabola, tedy funkce tvaru

$$f(x)=ax^2 + bx + c$$ Hlavním cílem experimentu je určit hodnotu koeficientu $a$ (tedy koeficient u $x^2$). Určete hodnotu tohoto koeficientu včetně nejistoty měření. Není potřeba provádět regresní diagnostiku.

• V přiloženém datovém souboru linreg2.csv naleznete výsledky určitého fyzikálního experimentu, ve kterém jsme měřili dvojice dat $(x_{i},y_{i})$. Naměřenými daty chceme proložit teoretickou funkci, kterou je v tomto případě logaritmická funkce, tedy funkce tvaru

$$f(x)=a + b \cdot \log{x} \, .$$ Hlavním cílem zpracování dat je vykreslit graf naměřených dat spolu s proloženou teoretickou závislostí. Vykreslete takovýto graf (včetně intervalového odhadu pro prokládanou funkci) a stručně ho okomentujte (takovýto graf musí mít všechny náležitosti). Není potřeba provádět regresní diagnostiku.

• Předpokládejme, že máme naměřeny dvojice dat $(x_{i},y_{i})$ a chceme jimi proložit lineární funkční závislost, tedy funkci tvaru

$$f(x)=a + bx \, .$$ Odvoďte přesnou podobu vzorce na výpočet hodnoty odhadů regresních koeficientů. Můžete použít libovolnou ze dvou metod představených v seriálu a také libovolné jiné zdroje, pokud je budete řádně citovat. Vzorec chceme opravdu odvodit (tj. uvést výpočet), nikoliv pouze napsat.

Bonus: V druhé a třetí úloze proveďte regresní diagnostiku a diskutujte, zda jsou splněny všechny potřebné předpoklady (pokud to jde, proveďte také test vhodnosti prokládané funkce a diskutujte jeho výsledky). Pro práci s daty použijte výpočetní prostředí R. Pro vyřešení těchto úkolů postačí drobně upravit přiložený skript, ve kterém je pomocí komentářů v kódu vysvětlena potřebná syntaxe jazyka R.

• skript v kódování UTF-8
• skript v kódování CP-1250
• vzor.csv
• linreg1.csv
• linreg2.csv

• Zkuste vlastními slovy popsat, k čemu a jak se používá testování hypotéz (postačí vlastními slovy popsat následující: hypotéza a alternativa, chyba 1. a 2. druhu, hladina testu, testová statistika, kritický obor testu, $p$-hodnota testu pro konkrétní naměřená data). Není potřeba uvádět přesná matematická odvození, stačí požadované pojmy a vlastnosti stručně popsat.
• V přiloženém datovém souboru testovani1.csv najdete naměřené hodnoty určité fyzikální veličiny. Pomocí jednovýběrového $t$-testu otestujte, zda je skutečná hodnota měřené fyzikální veličiny rovna $20$. Dále předpokládejme, že je naším cílem ukázat, že hodnota měřené fyzikální veličiny je větší než $20$. Použijte vhodnou jednostrannou modifikaci $t$-testu k tomu, abyste toto tvrzení ověřili (dejte si pozor na správné zvolení hypotézy a alternativy).
• V přiloženém datovém souboru testovani2.csv najdete naměřené hodnoty 2 různých fyzikálních veličin. Představujme si, že se jedná o měření stejné fyzikální charakteristiky ale za různých vnějších podmínek (teplota, tlak atd.). Pomocí dvouvýběrového $z$-testu otestujte hypotézu, že hodnota této fyzikální charakteristiky je pro obě volby vnějších podmínek stejná.
• Použijte stejná data jako v seriálové úloze z první série a pomocí Kolmogorovova-Smirnovova testu určete, který ze 4 vzorků dat pochází z normálního rozdělení a který vzorek pochází z exponenciálního rozdělení.

Bonus: Předpokládejte, že máte k dispozici měření 2 fyzikálních veličin (tedy 2 sady naměřených hodnot), kde jsou všechna měření na sobě nezávislá. Odvoďte upravený dvouvýběrový $z$-test, který by testoval hypotézu, že skutečná hodnota první měřené fyzikální veličiny je dvojnásobek skutečné hodnoty druhé měřené fyzikální veličiny. Pro udělení bodů je nutné a postačuje odvodit podobu testové statistiky a kritického oboru (Nápověda: Použijte vícerozměrnou verzi CLV, kde vhodně zvolíte funkci $f$, a dále postupujte analogicky jako u odvození klasického dvouvýběrového $z$-testu.).

Pro práci s daty použijte výpočetní prostředí R. Pro vyřešení těchto úkolů postačí drobně upravit přiložený skript, ve kterém je pomocí komentářů v kódu vysvětlena potřebná syntaxe jazyka R.

• skript v kódování UTF-8
• skript v kódování CP-1250
• testovani1.csv
• testovani2.csv

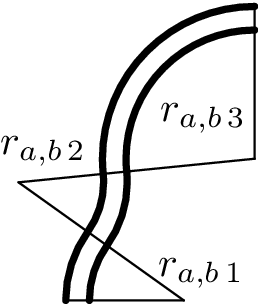
Do pekla vede cesta a silnice po opačných březích řeky. Jdeme po směru řeky, který je vyznačen na obrázku. Břehy řeky jsou tvořeny částmi soustředných kružnic. Pěší cesta kopíruje jeden břeh řeky, silnice druhý břeh, šířka toku je neměnná. Po jaké straně řeky je rychlejší jít? Známe středový úhel každého kružnicového oblouku $φ_{1}$, $φ_{2}$, $…$ a poloměr každé kružnice $r_{a1}$, $r_{b1}$, $r_{a2}$, $r_{b2}$, $…$, kde indexy $a$, $b$ značí levý a pravý břeh.

Představte si, že vezmete svou přítelkyni/svého přítele na večerní rande na pláž a sledujete západ slunce nad vzdálenou hladinou moře. Protože chcete prodloužit romantickou chvilku, vezmete si s sebou vysokozdvižný vozík, který se, jakmile slunce začne zapadat za obzor, začne rovnoměrným pohybem zvedat vzhůru, abyste stále viděli slunce dotýkající se horizontu. Jakou rychlostí se musí vozík pohybovat?