Vyhledávání úloh podle oboru
Databáze úloh FYKOSu odjakživa
astrofyzika (85)biofyzika (18)chemie (24)elektrické pole (71)elektrický proud (76)gravitační pole (81)hydromechanika (146)jaderná fyzika (44)kmitání (57)kvantová fyzika (31)magnetické pole (43)matematika (89)mechanika hmotného bodu (298)mechanika plynů (87)mechanika tuhého tělesa (221)molekulová fyzika (72)geometrická optika (78)vlnová optika (65)ostatní (167)relativistická fyzika (37)statistická fyzika (21)termodynamika (155)vlnění (51)
vlnění
2. Série 24. Ročníku - E. Jin a Young
Pravděpodobně jsme již všichni slyšeli o dvouštěrbinovém Youngově experimentu. Zkoušel si ale někdo z Vás podomácku „vyrobit“ interferenční proužky na stínítku osvětleném dvěma štěrbinami? K optickému Youngově pokusu existují i mechanická analogie, kdy sledujeme skládání dvou vlnění na vodě, nebo akustická analogie, kdy se skládají dvě zvukové vlny. Ve všech třech případech je možné zkoumat interferenční obrazec vznikající v určité rovině. Pokuste se realizovat jeden nebo i více z uvedených třech pokusů a získat tak interferenční obrazec. Poté určete vlnovou délku, případně rychlost šíření vlnění. Uvítáme fotodokumentaci.
ze Španělska posílá Marek
2. Série 24. Ročníku - P. šmoulové a Darth Vader
Po nadýchání se helia se člověku mění hlas tak, že mluví jako šmoula. Stejně to funguje, nadýcháte-li se vodíku (kuřáci, pozor!). Ale dá se dosáhnout i změny na hlas podobný Darthu Vaderovi, nejznámějším médiem je fluorid sírový. Jak funguje změna hlasu? Pokuste se ji kvantitativně odhadnout.
U chemiků sebral Michal
5. Série 23. Ročníku - E. ozvěna
Když stojíte v malém prostoru a zahrajete správný tón, můžete objevit jeho rezonanční frekvenci. Protože rezonanční frekvence přímo souvisí s rozměry rezonátoru, umíme je z její znalosti určit. Vyhlédněte si doma vhodnou místnost (ideální jsou malé rozměry a holé stěny; třeba toaleta), tímto způsobem ji změřte a porovnejte výsledky se skutečností.
na záchodě si notoval Jakub Michálek
6. Série 22. Ročníku - E. vratné lahve
Kupte si standardní skleněnou lahev od piva nebo minerálky a změřte, jak závisí výška tónu vydaného po fouknutí na hrdlo na výšce vodní hladiny v lahvi.
vymysleli organizátoři na pravidelné schůzi
5. Série 22. Ročníku - P. rámus
Pokuste se odhadnout, jakou energii přijme tělo návštěvníka rockového koncertu. Svůj odhad odůvodněte.
na schůzku donesl Honza Jelínek
2. Série 22. Ročníku - 4. do nekonečna a ještě dál
Bohatý vesmírný turista si zaplatil výlet do hlubokého vesmíru. Raketa vyletí ze Země a rovnoměrně zrychluje se zrychlením $a$, což si turista může ověřit například pouštěním míčku. Nudnou cestu si krátí zíráním ze zadního okénka, pozorováním Země. Po nějaké době (Jaké? Aspoň řádový odhad.) se mu začne zdát, že něco není v pořádku – Země se pomalu přestává zmenšovat. Z toho usoudí, že raketa zpomaluje, což neodpovídá tomu, že raketa stále má zrychlení $a$. To ale turistu nenapadne a rozlobeně jde za kapitánem požadovat vysvětlení. Co mu kapitán řekne?
Předpokládáme, že turista vidí celé elektromagnetické spektrum a má železné nervy a pozorování vydrží.
o prázdninách zkoušel Marek Pechal
2. Série 22. Ročníku - S. Young a vlnová povaha světla
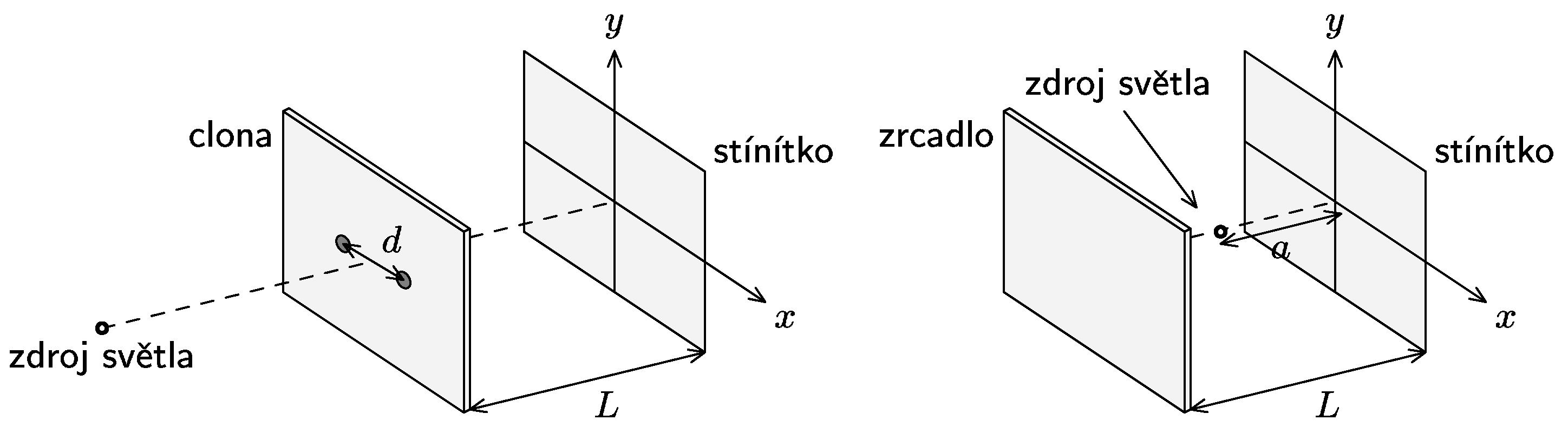
K zadání úlohy
- Jaký tvar interferenčních proužků na stínítku byste očekávali v následujících dvou sestavách? Najděte rovnice křivek maximální intenzity a zkuste jich několik načrtnout.
- Ukažte, jak by dopadl Youngův experiment, jestliže by se světlo chovalo podle Newtonových představ (tzn. difrakce ano, interference ne). nezapomeňte vzít v úvahu různý úhel dopadu světla na různá místa stínítka.
- Užitím vyloženého kvantověmechanického popisu určete rozložení intenzity, jaké by dostal Jöhnsson při použití čtyřštěrbiny (tedy čtyř úzkých rovnoběžných otvorů rozmístěných ve vzdálenostech $b$ od sebe). Načrtněte reprezentativní úsek grafu a okomentujte přednosti většího počtu otvorů.
Autoři seriálu
4. Série 21. Ročníku - 3. sopka burácí
Nedávno v televizi proběhl dokument o výbuchu sopky Krakatoa v srpnu 1883. Pozoruhodné je, že rachot výbuchu dočasně ohlušil lidi (nějakou dobu nic neslyšeli) ve vzdálenosti $50\,\jd{ km}$ od vulkánu. Dokonce byl slyšet jako vzdálené hřmění ve městě Alice Springs v centrální Austrálii, tj. asi $5 000\,\jd{ km}$ (slovy pět tisíc) od sopky.
Jaká byla hodnota akustického tlaku v $\jd{dB}$ v místě výbuchu? Můžeme předpokládat, že platí zákon úbytku intenzity se čtvercem vzdálenosti, či jaký zákon úbytku intenzity bude platit pro tento případ?
Úlohu vymyslel pan Janata inspirován zmíněným dokumentem.
6. Série 20. Ročníku - P. jak vypadají ufoni?
Zamyslete se nad tím, jestli by nějaké zvíře mohlo teoreticky komunikovat pomocí elektromagnetických vln rádiových frekvencí $(10\, \jd{Hz}\, –\, 100\, \jd{MHz}). Zkuste navrhnout, jak by vypadaly biologické ekvivalenty potřebných elektrických součástek.
Zadal Michael Komm doufaje, že přijdete na něco zajímavého.
5. Série 20. Ročníku - 1. smrt klavíristy
Z okna výškové budovy vypadl klavír i s klavíristou, který po celou dobu pádu hrál zděšené A. O $k$ pater pod tímto oknem odpočíval nebohý umývač oken. Jak velké je $k$, jestliže poslední, co umývač slyšel, bylo Ais, tedy tón o půltón vyšší? Rychlost zvuku v daném vzduchu je $347\, \jd{m\cdot s^{-1}}$, výška jednoho patra je $3,\!1\, \jd{m}$.
Morbidní úlohu navrhl Petr Sýkora.