Vyhledávání úloh podle oboru
Databáze úloh FYKOSu odjakživa
astrofyzika (85)biofyzika (18)chemie (24)elektrické pole (71)elektrický proud (76)gravitační pole (81)hydromechanika (146)jaderná fyzika (44)kmitání (57)kvantová fyzika (31)magnetické pole (43)matematika (89)mechanika hmotného bodu (298)mechanika plynů (87)mechanika tuhého tělesa (221)molekulová fyzika (72)geometrická optika (78)vlnová optika (65)ostatní (167)relativistická fyzika (37)statistická fyzika (21)termodynamika (155)vlnění (51)
mechanika hmotného bodu
3. Série 1. Ročníku - 3. tramvaj
Ve stojící tramvaji visí u svislé desky na niti délky $l$ citrón o hmotnosti $m$ (předpokládáme, že rozměry citrónu jsou velmi malé v porovnání s délkou niti). Tramvaj se rozjede se zrychlením $a$, které můžeme považovat za konstantní. Spočtěte, kam až toto kyvadlo vykývne (jaký maximální úhel bude svítat s deskou) a kdy citrón opět ťukne do desky.
3. Série 1. Ročníku - E. přetahovaná
Na kulatý sloup či tyč je namotáno několik závitů lana. Z jedné strany drží lano třeba malé dítě a táhne za něj malou silou $F_{d}$ (třeba $1\; \textrm{N}$). Z druhé strany táhne za lano obr. Jak velkou silou může obr za lano táhnout, aniž by dítě na druhém konci „přetáhl“? Předpokládáme, že sloup se nemůže otáčet.
Zkuste výsledek odvodit teoreticky, ale zejména vyšetřete daný problém experimentálně. (Jaká je závislost síly na materiálech sloupu a lana, velikosti sloupu, počtu závitů – a má např. smysl „neceločíselný“ počet závitů? Atd., atd. Obra i dítě můžete nahradit jinými pomůckami, sloup také.)
2. Série 1. Ročníku - 1. silák
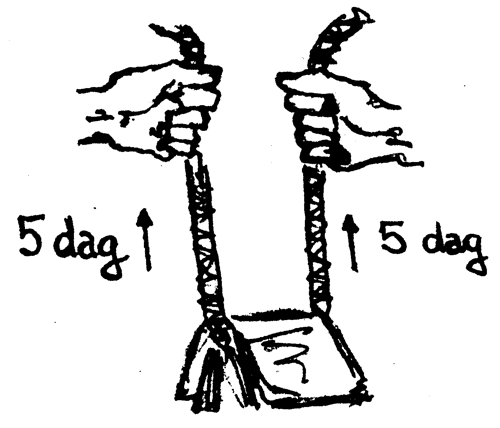
Uvolněné lano

Vodorovně napnuté lano
Za devatero horami je země, v níž se síla měří v jednotkách zvaných $\textrm{dag}$. Na pouti tam silák napíná oběma rukama lano, na němž je zavěšen telefonní seznam o tíze $10\; \textrm{dagů}$. (Kdyby silák držel oba konce provazu u sebe, napětí v obou částech lana by bylo $5\; \textrm{dagů}$.) Jaké bude napětí v obou částech lana, když silák roztáhne lano do vodorovné polohy?
- $5\; \textrm{dagů}$
- $10\; \textrm{dagů}$
- $20\; \textrm{dagů}$
- více než milión $\textrm{dagů}$
2. Série 1. Ročníku - 2. čluny

Pohled na čluny
Obrázek ukazuje dva čluny pohybující se po hladině jezera. Z obálky vln soudíme, že
- obě lodi plují větší rychlostí, než je rychlost povrchových vln, přičemž loď I pluje rychleji než loď II
- loď I pluje rychleji než loď II, ale nemusí nutně plout větší rychlostí, než je rychlost povrchových vln
- ani a), ani b)
2. Série 1. Ročníku - 3. Křemílek

Miska s Křemílkem a kuličkou
Křemílek chce dostat z misky těžkou kuličku. Stěny misky jsou však příliš strmé, aby ji vykulil přímo. Svými silami
- může dostat kuličku ven. (Jak?)
- nemůže dostat kuličku ven.
2. Série 1. Ročníku - S. odpor působící na auto
Spočtěte, jak bude s časem klesat rychlost auta brzděného jen odporem vzduchu. Auto jede po rovině na neutrál a zanedbáme valivé tření kol atd. – vše kromě odporu vzduchu.
Návod: Síla, kterou je auto brzděno, je v daném případě zhruba úměrná druhé mocnině jeho rychlosti: $F_{brzd}=C\cdot v$. (Pro běžný automobil lze odhadnout $C=(1–2)\; \textrm{m}^{-2}\cdot \textrm{s}$.) Uvažte, že během krátkého časového intervalu $Δt$ se síla působící na automobil příliš nezmění a jeho pohyb tedy můžeme brát jako rovnoměrně zpomalený. Celkovou změnu rychlosti za delší čas dostaneme poskládáním změn v jednotlivých „kouscích“ $Δt$.
Problém tak lze velmi dobře simulovat na mikropočítači, ale můžete využít i obyčejnou kalkulačku a hodnoty psát na papír, vynášet do grafu apod. Úlohu si můžete i rozšířit a počítat též ujetou dráhu, případně uvažovat změněné podmínky: jízdu z kopce či do kopce, jízdu pod vodou ($Cρ_{prostředí}$), vynalézavosti se meze nekladou.
1. Série 1. Ročníku - 2. antiraketa
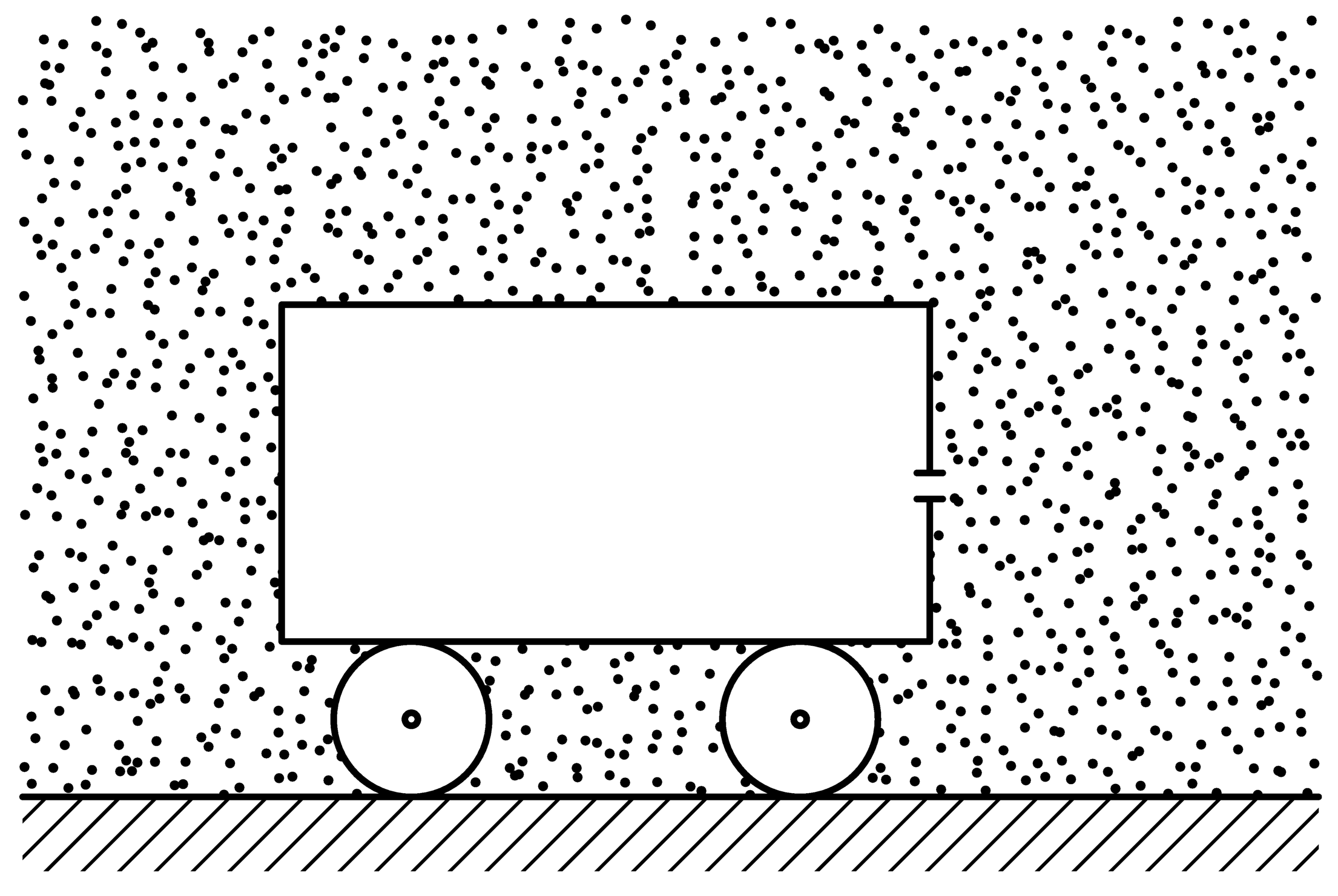
Model nádoby
Uvažujme nádobu s otvorem dle obrázku. Uniká-li stlačený vzduch z nádoby ven, nádoba se pohybuje. Jde o princip analogický raketovým motorům. Představme si nyní opačnou situaci. Nádobu, v níž bylo vakuum, umístěnou ve vzduchu, který do nádoby proudí malým otvorem. Nádoba se bude pohybovat:
- doleva
- doprava
- nebude se pohybovat
1. Série 1. Ročníku - E. odpor vzduchu
Pohybuje-li se těleso v kapalném nebo plynném prostředí, působí na něj prostředí odporující silou, závislou na rychlosti tělesa. Navrhněte nějakou jednoduchou metodu (realizovatelnou doma, ve škole atp.), kterou by bylo možno alespoň přibližně určit závislost rychlosti tělesa pohybujícího se ve vzduchu. Navržené experimenty proveďte a zhodnoťte výsledky.
Návod: Předpokládejte závislost tvaru $F = av^{b}$.