Vyhledávání úloh podle oboru

Předtím, než byl dosažen a překročen okraj Zeměplochy a začaly být podnikány vědecké výpravy za potvrzením existence čtyř slonů, želvy a určení jejího pohlaví, si některé primitivní kmeny myslely, že síla, která je drží na Zeměploše, je dána superhustou deskou z koncentrovaného bylonebylia. Byla to opravdu velice primitivní představa, protože jak dnes již víme, například výprava, která potvrdila existenci želvy, neslavně dopadla tak, že se jejich člun utrhl a upadl. Tedy vlastně nedopadl… Nicméně by nás zajímalo – jakou plošnou hustotu by bývala byla musela taková deska mít, aby na povrchu Zeměplochy blízko jejímu středu byl obyčejný předmět, při zanedbání magie, přitahován stejnou silou, jakou je gravitační síla na povrchu Zemneplochy? Uvažujte, že superhustá deska je opravdu velice tenká, a jak tvrdí pověsti, je umístěna $H=8^{4}\;\mathrm{m}=4\,096\;\mathrm{m}$ pod povrchem Zeměplochy. Deska má být dle bájí homogenní a hmotnosti jiných těles zanedbatelné. Zanedbejte pohyby želvy a slonů. Za Zemneplochu si dosaďte slovo Země, pokud jste nečetli dílo autora, pro kterého si přišel Smrť. Zeměplocha má pro účely této úlohy průměr přibližně přesně $d=10\,000\;\mathrm{km}$.

Máme dvě homogenní nerotující planety tvaru dokonalých koulí s vnějšími poloměry $R_{Z}$. První z nich je dokonalá koule o hustotě $ρ$ a na jejím povrchu je gravitační zrychlení $a_{g}$. Druhá je dutá do poloviny jejího poloměru a až pak je plná.

• Pokud by obě planety byly ze stejného homogenního materiálu, na povrchu které planety bude větší gravitační zrychlení a jaký bude poměr mezi hodnotami gravitačního zrychlení na obou planetách?
• Pokud by i na povrchu druhé planety bylo gravitační zrychlení $a_{g}$, jaká by musela být hustota druhé planety?

Faleš chtěl v Praze (V Holešovičkách 2 v přízemí) určit hodnotu gravitačního zrychlení z experimentu, kdy pouštěl kulatý míček z výšky pár metrů na Zemi. Rozmyslete si, jaké korekce musel při zpracování měření zahrnout. Poté navrhněte vlastní experiment na stanovení gravitačního zrychlení a diskutujte jeho přesnost.

Máme dřevěnou kuličku ve výšce $h=1\;\mathrm{m}$ nad Zemí o poloměru $R_{Z}=6\,378\;\mathrm{km}$ a hmotnosti $M_{Z}=5,\!97\cdot 10^{24}\;\mathrm{kg}$. Kulička má poloměr $r=1\;\mathrm{cm}$ a je ze dřeva o hustotě $ρ=550\;\mathrm{kg}\cdot \mathrm{m}^{-3}$. Předpokládejte, že Země má náboj $Q=5\;\mathrm{C}$. Jaký náboj $q$ by musela mít kulička, aby se mohla vznášet nad Zemí? Jak tento výsledek závisí na výšce $h?$

Jak by musel být minimálně dlouhý ocelový drát ve stočeném stavu, aby se při volném zavěšení za jeho jeden konec přetrhl? Používáme ocelový drát o hustotě $ρ=7900\;\mathrm{kg}\cdot \mathrm{m}^{-3}$, průměru $D=1\;\mathrm{mm}$ a mezi pevnosti $σ_{max}=400\; \jd{MPa}$. Uvažujte, že jsme v homogenním tíhovém poli o intenzitě $g=9.81\;\mathrm{m}\cdot \mathrm{s}^{-2}$.

Bonus: Uvažujte teď nejdelší drát, který se ještě nepřetrhne. O kolik procent se protáhne po zavěšení? Youngův modul pružnosti v tahu použité oceli je $E=200\;\jd{GPa}$.

Odhadněte, kolik energie by bylo potřeba na odpaření všech pozemských oceánů.

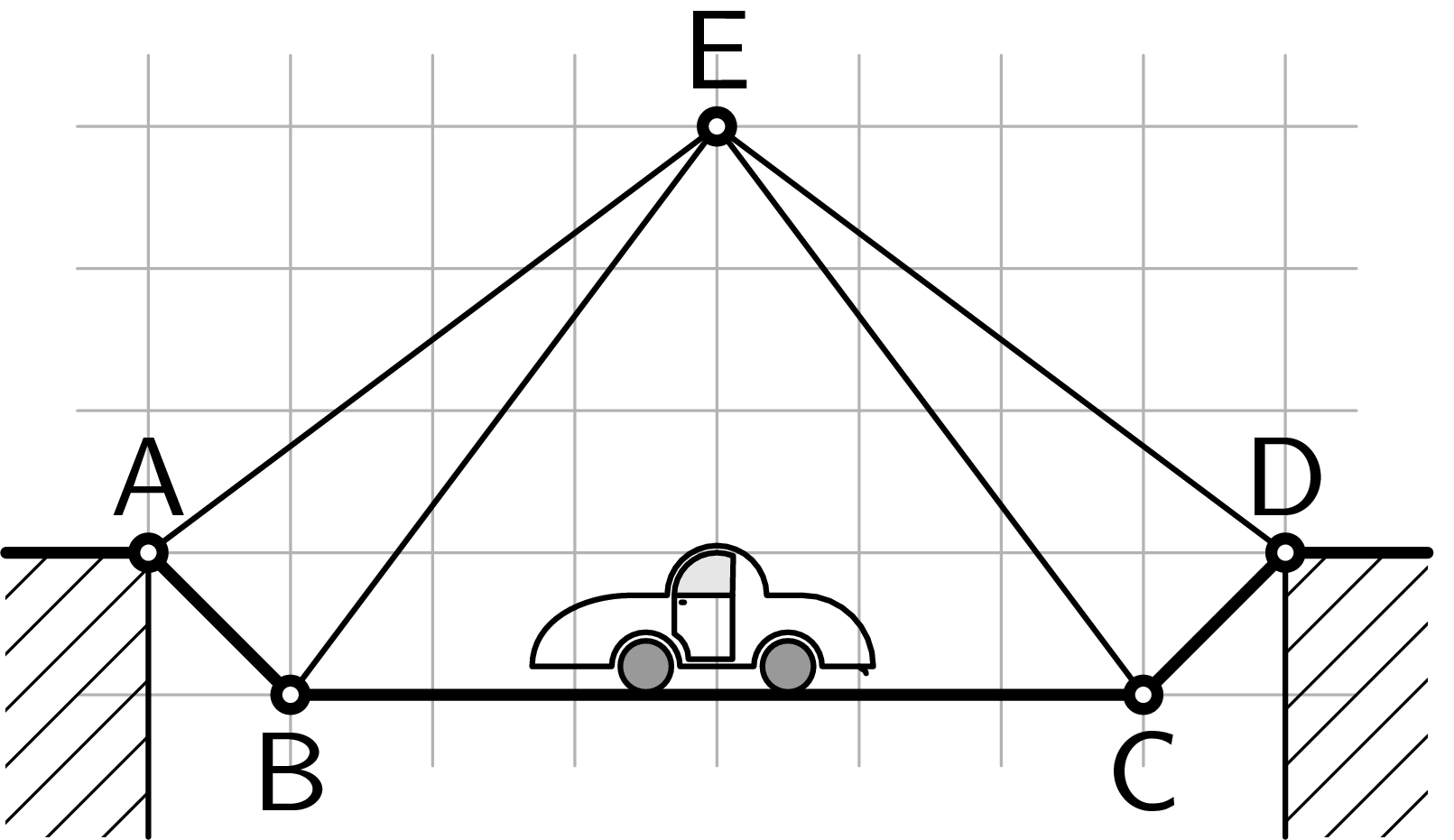
Mějme dvourozměrnou část jednoduché mostní konstrukce jako na obrázku tvořenou z tyčí spojených v bodech $A$, $B$, $C$, $D$ a $E$. Zjistěte, které tyče jsou namáhány tlakem a které tahem a jak velkými silami, pokud jsou tyče nehmotné a na tyči $BC$ stojí autíčko o hmotnosti $m$. Délky tyčí určete z obrázku.

Bonus: Uvažujte, že všechny tyče mají konstantní délkovou hustotu $λ$.

V pohádce Mrazík vyhodil Ivan loupežníkům kyje do takové výšky, že spadly až za půl roku. Jak vysoko by je musel vyhodit, aby dopadly za takovou dobu? Vytvořte první a druhý hrubý odhad. Zdůvodněte, proč jsou tyto odhady nejspíš řádově špatné. Co jste všechno zanedbali? Z jakých důvodů je celkově nesmyslné, aby kyje dopadly na prakticky stejné místo po půl roce? Nebraňte se proudu kritiky na tuto klasickou pohádku!

Co kdyby se „přes noc“ změnila hodnota gravitační konstanty na dvojnásobek a přitom by zůstaly zachovány ostatní fyzikální konstanty na původních hodnotách? A co kdyby se zvětšila stokrát? Rozepište se o různých aspektech – zejména o životě na Zemi a drahách vesmírných objektů.

Odhadněte, jakou minimální energii musíme dodat kosmické stanici, abychom ji dostali na oběžnou dráhu. Můžete pracovat s hodnotami pro mezinárodní kosmickou stanici ISS, která obíhá Zemi ve výšce cca $h=350\;\mathrm{km}$ a má celkovou hmotnost přibližně $m=450\;\mathrm{tun}$. Vysvětlete, proč je odhad minimální a vyjmenujte alespoň některé fyzikální skutečnosti, které vedou k tomu, že je skutečná spotřeba raket významně vyšší.