Vyhledávání úloh podle oboru

• sedimentace krve

Zkuste přibližně spočítat jak rychle probíhá sedimentace lidské krve (usazení zdravých červených krvinek na dně nádoby). Dynamická viskozita $η$ krevní plazmy při 37 °C je přibližně $2\, \jd{N\cdot s\cdot m^{-2}}$ (běžně se měření sedimentace provádí tak, že se krev nechá odstát na jednu hodinu a poté se změří výška již usazených krvinek – bývá obvykle okolo 10 mm).

Nápověda: mohl by se hodit Stokesův vztah pro odporovou sílu $F = 6 π η r v$, který platí pro laminární proudění.

• nevěřte vlastním očím

Aleš jel v poledne tramvaji po nábřeží kapitána Jaroše v Praze směrem na Malou Stranu. Seděl u okna a přímo z jiho-jihozápadu na něj svítilo slunce. Protože se díval před sebe, jedno oko měl ve stínu vlastního nosu. Když ale uhnul očima doprava, zjistil, že levým okem vnímá mírně jiné odstíny barev než pravým. Do jakého odstínu se mu vidění v levém oku zabarvilo a proč?

Chceme-li na monitoru počítače zobrazit azurovou barvu, musíme rozsvítit červený a modrý segment. Azurová barva odráží v nejjednodušším případě světlo dvou vlnových délek (modré a červené), dále pokud budeme mít modrou barvu, tak tato bude odrážet modré světlo a červená obdobně. Když smícháme modrou a červenou temperu, výsledná směs bude mít fialovou barvu, protože modrá složka pohltí vše až na modrou a obdobně také červená. Proto ze směsi těchto barev budeme pozorovat pouze ty vlnové délky, které odrážejí obě složky. Představte si, že tempery jsou složeny z malých kapiček. Jak bude záviset výsledný zrakový vjem na jejich velikosti?

Změřte, jak závisí průsvitnost papíru na úhlu, pod kterým je sklopený. Máme soustavu oko papír žárovka v jedné přímce. Měříme závislost intenzity prošlého světla na úhlu stočení papíru vzhledem k ose aparatury.

Pravděpodobně jsme již všichni slyšeli o dvouštěrbinovém Youngově experimentu. Zkoušel si ale někdo z Vás podomácku „vyrobit“ interferenční proužky na stínítku osvětleném dvěma štěrbinami? K optickému Youngově pokusu existují i mechanická analogie, kdy sledujeme skládání dvou vlnění na vodě, nebo akustická analogie, kdy se skládají dvě zvukové vlny. Ve všech třech případech je možné zkoumat interferenční obrazec vznikající v určité rovině. Pokuste se realizovat jeden nebo i více z uvedených třech pokusů a získat tak interferenční obrazec. Poté určete vlnovou délku, případně rychlost šíření vlnění. Uvítáme fotodokumentaci.

• Index lomu v nelineárním materiálu závisí na intenzitě světla $I$ jako $n=n_{1}+n_{2}I$, kde $n_{1}$ a $n_{2}$ jsou konstanty větší než nula. Zamyslete se, co se bude dít s paprskem světla dané šířky, který tímto materiálem prochází. Předpokládejte, že intenzita paprsku klesá se vzdáleností od jeho středu. (Stačí kvalitativní úvaha, odvážnější se mohou pokusit vybudovat analytický model.)

• Deska tloušťky $a$ sestává z 2$N$ stejně širokých rovnoběných destiček ze dvou materiálů o indexech lomu $n_{1}$ a $n_{2}$ poskládaných na střídačku. Světelná vlna dopadá kolmo na čelní destičku. Jaký bude efektivní index lomu této smíchané desky pro $N→∞?$ Napadá vás proč? ( Nápověda: pro libovolnou matici $A$ platí $\rm{lim}_{N→∞}(I+A⁄N)^{N}=\exp(A)$, kde $I$ je jednotková matice a exp$(A)=I+A+A⁄2!+A⁄3!+\ldots)$

• Co se stane, když do krystalu kalcitu kolmo posvítíme kruhově polarizovaným světlem?
• Představte si, že je právě čas $t=0$, široko daleko není žádný náboj

($ρ=\textbf{j}=0)$, a my známe počáteční elektromagnetické pole v celém prostoru $\textbf{E}(\textbf{r},0)$ a $\textbf{B}(\textbf{r},0)$. Z rovnic (14) a (15) tedy můžeme vyjádřit časové derivace $∂\textbf{B}⁄∂t$ a $∂\textbf{E}⁄∂t$ pomocí prostorových a vypočítat tak $\textbf{E}$ a $\textbf{B}$ v následujícím okamžiku. Tento postup můžeme iterativně opakovat a dostat tak celý časový vývoj pole pro $t>0$. Jak je možné, že vůbec nemusíme použít první a druhou Maxwellovu rovnici?

• Uvažujte náboj velikosti $q$, který je v klidu pro $t\lt0$, a v čase $t=0$ na něj začne dopadat rovinná světelná vlna. Jak se bude náboj následně pohybovat, když světlo je polarizované (i) lineárně (ii) kruhově? Promyslete nejprve kvalitativně, přesný výpočet, případně počítačová simulace obdrží bonus.

Jak nejdále od sebe mohou být dva lidé, aby je nikdo třetí na Zemi nerozeznal, kdykoliv jsou viditelní? Nezapomeňte, že lidé jsou bodové světelné zdroje ve výšce 2 m a Země je koule.

Jak roste hlasitost (definujte si sami) sboru s počtem jeho členů? Co z toho plyne? Členy sboru uvažujte jako bodové zdroje zvuku stejné amplitudy a frekvence, ale posunuté o náhodnou fázi. Všichni bodoví zpěváci se nacházejí v jednom místě.

• V textu seriálu jsme pracovali s diskrétním rozložením bodových zdrojů na přímce a jejich zobrazením na přímku. Nyní si představte, že máte zdroje světla rozložené na rovině a stínítko je rovina na ni rovnoběžná. Popište rozložení intenzity na stínítku v případě, že zdroje světla:

• Leží na jedné přímce s pravidelným intervalem $d$.

• Jsou rovnoběžné přímky, kde vzdálenost mezi sousedními přímkami je $d$.

• Leží ve vrcholech obdélníkové sítě, kde obdélníky mají strany $a$, $b$.

• Mějme následující situaci: Před stínítkem, reprezentovaném nějakou rovinou $xy$ je disk o poloměru $R$, rovnoběžně s rovinou. Ze strany disku na stínítko svítíme z nekonečna světlem, tzn. všechny paprsky jsou navzájem rovnoběžné

a kolmé na rovinu $xy$. Vysvětlete, proč situaci můžeme popsat pomocí bodových zdrojů světla spojitě rozložených všude na rovině ve které leží disk kromě disku samotného, najděte závislost intenzity světla na rovině $xy$ jako funkci $x$ a $y$ (není potřeba uzavřený tvar, stačí ve tvaru integrálu) a ukažte, že v bodě, který je na rovině $xy$ přímo naproti středu disku se děje něco, co bychom z hlediska geometrické optiky nečekali.

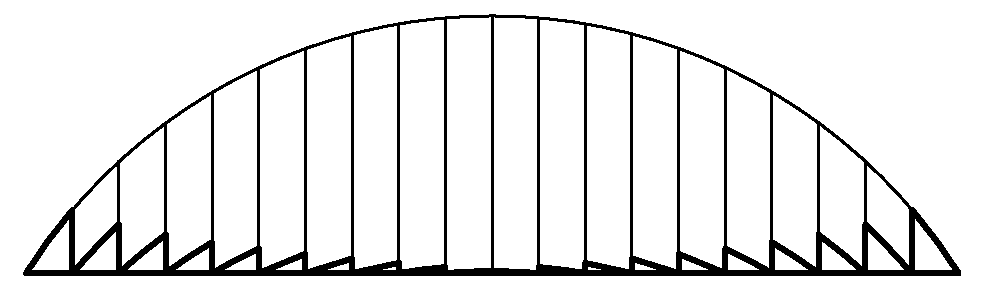
Možná jste si všimli, že mezi zdrojem a průhlednou podložkou na fólie je v tradičním meotaru za účelem soustředění světla vložená dost zvláštní čočka, která vypadá spíš jako rýhovaná deska (viz také úloha VI.2 ze XVII. ročníku). Vznikne tak, že standardní ploskovypuklou čočku rozřezáme na soustředné prstence, z každého si necháme jen úplný konec a výsledek opět složíme, takže získáme něco jako „osově symetrické pahorkaté sklo“ (viz obrázek).

Takto vzniklá čočka má všude stejný sklon jako původní spojka, a podle Snellova zákona tak očekáváme, že bude stejně dobře soustřeďovat světlo. Naproti tomu, z pohledu Fermatova principu, už každé dráze nepřísluší stejný čas, neboť jsme v různých místech odebrali různě tlusté vrstvy skla – například úplně nejkratší čas teď odpovídá cestě po optické ose. Zdá se tedy, že Fermatův pricnip selhává – podle něj by čočka soustřeďovala jen světlo jdoucí po optické ose a nefungovala tak, jak má. Rozhodněte kdo má pravdu: Snell, Fermat? A proč?

• Najděte dráhy paprsků ve dvojrozměrné situaci, kdy závislost indexu lomu na vzdálenosti $r$ od počátku je dána funkcí

$n(r)=n_{0}⁄(1+(r⁄a))$.

• Bonus: Vložíme-li do prostoru s proměnlivým indexem lomu bodový zdroj světla,

může se stát, že se velká část paprsků, které z něj vycházejí, sejde v jednom bodě, jako je tomu v případě spojné čočky. Takto vzniklý bod pak nazýváme obrazem bodu původního. Popište geometrické zobrazení $zdroj→obraz$, které tímto způsobem indukuje prostředí s indexem lomu z předchozí úlohy.