Vyhledávání úloh podle oboru
Databáze úloh FYKOSu odjakživa
astrofyzika (85)biofyzika (18)chemie (24)elektrické pole (71)elektrický proud (76)gravitační pole (81)hydromechanika (146)jaderná fyzika (44)kmitání (57)kvantová fyzika (31)magnetické pole (43)matematika (89)mechanika hmotného bodu (298)mechanika plynů (87)mechanika tuhého tělesa (221)molekulová fyzika (72)geometrická optika (78)vlnová optika (65)ostatní (167)relativistická fyzika (37)statistická fyzika (21)termodynamika (155)vlnění (51)
astrofyzika
(6 bodů)4. Série 25. Ročníku - S. seriálová
- Spirální galaxie můžeme velmi hrubě popsat logaritmickou spirálou $r(\phi)=r(0)\exp(\phi\tan Φ)$, kde $r$ a $φ$ jsou polární souřadnice a $Φ$ je úhel otevření odpovídající úhlu, který svírá kolmice k průvodiči s tečnou ke spirále (úhel otevření roste ve směru hodinových ručiček, vyjadřujeme jej v radiánech, přičemž hodnota může nabývat více než $2π$). Uvažujme $Φ = 10°$. Odvoďte vztah pro poměr vzdáleností dvou sousedních závitů téhož spirálního ramene od centra galaxie. Jak by se poměr změnil, kdyby ramena byla čtyři (rovnoměrně rozložená). Vyjádřete vzdálenost pro sousední ramena v $r(0)=8 \;\mathrm{kpc}$.
- Uvažujte nekonečný vesmír s konstantní hustotou hvězd a bez extinkce. Vyjádřete vztahy pro integrální a diferenciální počet hvězd v závislosti na zdánlivé hvězdné velikosti. Co se stane, bude-li zdánlivá hvězdná velikost velká?
- Bonus: Jaká je pravděpodobnost, že dvě hvězdy se nám v galaxii promítnou za sebe? Uvažujte osamocené hvězdy, ne dvojhvězdy.
(6 bodů)3. Série 25. Ročníku - S. hvězdný zvěřinec
- Proč je třeba, aby byl molekulární mrak, ze kterého jsou tvořeny hvězdy, chladný? Zkuste odhadnout a zdůvodnit rozumnou teplotu.
- Podíváme-li se na HR diagram některé z hvězdokup, najdeme velký rozptyl okolo hlavní posloupnosti. Jaké jsou způsoby, jak takový rozptyl může vzniknout? Ilustrační obrázek pro hvězdokupu Plejády, M45 najdete třeba tady.
- Jak dlouho by žila hvězda, kdyby nebyla živena termonukleárními reakcemi, jen energií ze smršťování se?
- Planetární mlhovina Helix má průměr 16' a nachází se ve vzdálenosti cca 213 $\;\mathrm{pc}$ od Země. Jaký je její skutečný poloměr a jak je stará, pokud se její obálka rozpíná s rychlostí 20 $\;\mathrm{km/s}$.
Janapka.
(6 bodů)2. Série 25. Ročníku - S. vzdálenosti a černé těleso
- Absolutně černé těleso z definice pohltí všechno světlo, co na něj dopadne, ve všech vlnových délkách. Zároveň je to ideální zářič s charakteristickým spektrem. Můžeme si ho představit třeba jako temné okno domu. Slunce však na první pohled enegrii pouze vydává. Jak je tedy možné, že jeho zážení lze v prvním přiblížení aproximovat absolutně černým tělesem?
- V textu jsme vyjádřili Planckovu funkci jako funkci vlnové délky a teploty. Zkuste ji vyjádřit v závislosti na teplotě a frekvenci. Dokažte, že pro velké vlnové délky a vysoké teploty Planckova funkce přechází v Raighleyův-Jeansův zákon $B_{λ}(T)=2ckT/λ^{4}$ a naopak ve Wienův zákon $B_{λ}=2hc^{2}/λ^{5}$ $\exp(-hc/λkT)$ pro nízké teploty a malé vlnové délky.
- Kruh, který napozoroval Hubbleův vesmírný dalekohled v supernově SN1987A, má podél hlavní poloosy úhlový průměr 1,66''. Má jít o cirkulární objekt, který je díky natočení vůči nám pozorován jako elipsa (viz zde). Světlo ze vzdálenější části elipsy doletělo k Zemi o 340 dnů později, než z bližšího konce. Proměřte fotografii a určete úhel natočení vůči pozorovateli a zkuste spočítat poloměr kruhu. S pomocí trigonometrie určete vzdálenost objektu.
- Pro určení červeného posuvu se zpravidla používají spektrální čáry vodíku. Odhadněte, do jaké hodnoty červeného pousuvu $z$ se pomocí spekter můžeme dostat. Zkuste zjistit (nebo navrhnout), jak se měří $z$ u vzdálenějších objektů.
Janap.
(6 bodů)1. Série 25. Ročníku - S. seriálová
- Některé hvězdy jsou považovány za obtočné, čili cirkumpolární. Znamená to, že jsou vidět po celý rok? Jaké hvězdy jsou v našich zeměpisných šířkách vidět po celý rok? Jaká souřadnice nám cirkumpolární hvězdy označuje? Jaká je situace u nás, na pólu a na rovníku? Pro ilustraci doporučujeme stáhnout program Stellarium (www.stellarium.org, licence GNU GPL, takže program je ke stáhnutí zdarma), kde si můžete zadat jakoukoliv zeměpisnou polohu a podívat se na jednotlivé situace.
- Srovnejte absolutní hvězdnou velikost nejjasnější hvězdy letní oblohy, Vegy ($α$ Lyr, 7.76 $\;\mathrm{pc}$ daleko, zdánlivá hvězdná velikost -0,01 $\;\mathrm{mag}$) a Betelgeuze ($α$ Ori, 200 $\;\mathrm{pc}$ daleko, zdánlivá hvězdná velikost 0.42 $\;\mathrm{mag}$). Jak by se nám hvězdy jevily, kdyby si vyměnily vzdálenosti? Diskutujte viditelnosti.
- Transformace a zase transformace. Zkuste si spočítat transformaci mezi galaktickými a ekvatoriálními souřadnicemi II. druhu. Výrazy nemusíte upravovat do verze uvedené v literatuře.
- Janap má ve zvyku občas se ztratit. Ona za to nemůže, občas se to stane. Tentokrát však s sebou měla theodolit. Zázračnou krabičku, která umí určit výšku hvězd nad obzorem. Změřila si polohy hvězd Arcturus a Capella a zaznamenala přesný čas. Arcturus měl 123.20 $\;\mathrm{grad}$ v 18:46:30, Capella 113.60 $\;\mathrm{grad}$ v 19:18:30. Kdepak se Janap nacházela? (Nezapomeňte, že výška hvězd je uváděna v gradech, horizont je na úrovni 100 $\;\mathrm{grad}$, plný úhel je 400 $\;\mathrm{grad}$).
Janapka.
6. Série 24. Ročníku - 4. konečné řešení otázky globálního oteplování
Jak by se změnil výkon slunečního záření dopadajícího na Zemi v odsluní, když by byla jednorázově vychýlena zemská dráha (změnou její okamžité rychlosti ve směru její dráhy) tak, aby byl pozemský rok o týden delší? Odhadněte teplotu Země v přísluní a odsluní, pokud by Země měla téměř nulovou tepelnou kapacitu. Stačí uvažovat, že původní dráha Země byla kruhová a přešla na eliptickou.
Karel se díval na Futuramu
5. Série 24. Ročníku - 2. Měsíc jako lodička
Z jakých míst na Zemi a kdy vypadá Měsíc jako lodička? (jeho cípy jsou rovnoběžné s obzorem, osa symetrie je kolmá k místnímu nebeskému poledníku) Pokud si s řešením nevíte rady, můžete si nainstalovat vhodný software (např. Celestia) a celou situaci si prohlédnout z různých míst na zemi.
Terka J. se jednou ve čtyři ráno zasněně dívala na Měsíc
1. Série 24. Ročníku - 1. rozcvička
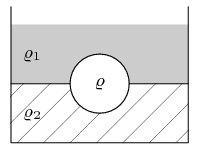
- mezi vodami
Na rozhraní dvou nemísitelných kapalin se vznáší pevná homogenní koule o hustotě ρ (viz obrázek). Horní kapalina má hustotu $ρ_{1}$, dolní $ρ_{2}$, přičemž víte, že $ρ_{1} < ρ < ρ_{2}$. Jaká část objemu koule se nachází v horní a jaká v dolní kapalině?
- sesterská planeta
V posledních několika letech již byla objevena spousta planet ležících mimo Sluneční soustavu. Daleko zajímavější by bylo ovšem objevovat planety, které jsou podobné Zemi. Předpokládejte, že chcete objevit podobnou Zemi (terestrická planeta s podobným poloměrem jako Země), která obíhá svou hvězdu podobnou Slunci (stejná spektrální třída – podobná hmotnost, podobný poloměr) jednou za pozemský rok. Předpokládejte, že tato soustava je vzdálená od našeho Slunce zhruba 10 pc. Určete podmínky, za kterých by šlo pozorovat planetu přímo z poklesu jasnosti hvězdy a odhadněte dobu, na kterou tato situace nastane. Jak se zkomplikuje hledání takové hvězdy, když soustava bude mít víc planet?
Z ruských bylin vyčetl Marek a po hvězdných dálavách zatoužil Karel.
1. Série 22. Ročníku - P. Mikuláš vs. Klaudios
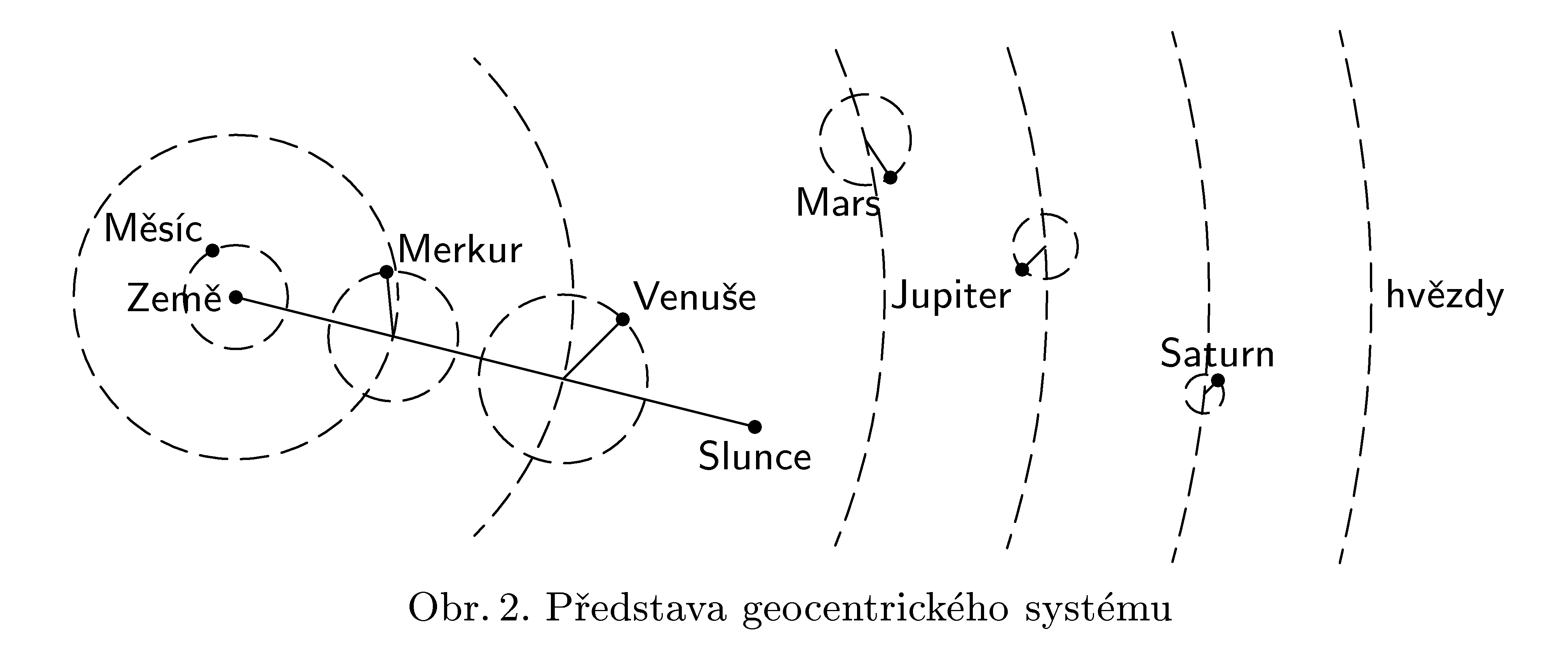
Představa geocentrického systému
Rok 2009 je vyhlášen jako Mezinárodní rok astronomie a připomíná 400 let používání dalekohledů lidstvem. Vraťme se o čtyři staletí zpět, kdy byl dalekohled již k dispozici, ale klasická fyzika ještě v plenkách. V otázce uspořádání světa spolu soupeřily Koperníkův heliocentrický názor a Ptolemaiův geocentrický systém. Navrhněte experiment, resp. pozorování, které mezi oběma představami dokáže rozhodnout. Dostatečně okomentujte, jaký výsledek lze očekávat a co z něj plyne v prospěch či neprospěch uvažovaných uspořádání. Vlastní pozorování není nutné, i když vhodné. Navíc vysvětlete, proč jsou v geocentrickém modelu Slunce a Země spojeny úsečkou?
Významný důkaz chtěl připomenout Pavel Brom.
5. Série 21. Ročníku - 4. sluneční konzerva
Ráma cestuje mezi hvězdami tak, že polovinu času rovnoměrně zrychluje a polovinu času rovnoměrně zpomaluje. Právě se pohybuje kolem Slunce po parabole s vrcholem na orbitě Země. Energii získává ze slunečního záření (žádný reaktor nebo obří baterie jsi na něm neobjevil) a jeho povrch absorbuje 80 % dopadající energie. Nasbírá při průletu sluneční soustavou dostatečnou energii, aby se dostal k Siriu, který je vzdálen 12 světelných let, za 24 let?
Nadhodil Jakub Benda
5. Série 21. Ročníku - S. posloupnosti, horká dutina a bílý trpaslík
- Odvoďte Taylorův rozvoj exponenciály a pro $x=1$ graficky znázorněte posloupnost částečných součtů řady $\sum_{k=1}^{∞}1⁄k!$ spolu s posloupností ${ ( 1 - 1 ⁄ n)^{n}}_{n=1,2,\ldots}$.
Stejným způsobem porovnejte posloupnost ${ ( 1 - 1 ⁄ n)^{n}}_{n=1,2,\ldots}$ a posloupnost částečných součtů řady $\sum_{k=1}^{∞}x^{k}⁄k!$, čili posloupnost ${\sum_{k=1}^{n}x^{k}⁄k!}_{n=1,2,\ldots}$, tentokráte však pro $x=-1$.
- Druhý úkol bude určit závislost koncentrace elektronů a pozitronů na teplotě při celkovém náboji $Q=0$ v prázdné uzavřené horké dutině.
(Bude-li se vám chtít, i při jiných vámi zvolených hodnotách $Q.)$ Dále určete závislost poměru vnitřní energie $U_{e}$ elektronů a pozitronů ku celkové vnitřní energii systému $U$ (tj. součtu energie elektromagnetického záření a částic) na teplotě a určit hodnoty teploty odpovídající některým význačným hodnotám tohoto poměru (např. 3 ⁄ 4, 1 ⁄ 2, 1 ⁄ 4, …; může tento poměr nabývat všech těchto hodnot?).
Pokuste se své výsledky pěkně graficky zpracovat ve formě grafů (můžete zkusit i trojrozměrné).
Při vašem snažení vám může hodně pomoci, pokud si zavedete vhodné bezrozměrné jednotky (např. $βE_{0}$ místo $β$ apod.).
- Řešte soustavu diferenciálních rovnic pro $M(r)$ a $ρ(r)$ v modelu bílého trpaslíka pro několik vhodně zvolených hodnot $ρ(0)$
a pro každou z nich sledujte hodnotu, ke které se blíží $M(r)$ při $r→∞$. Ta je zřejmě rovna hmotnosti celé hvězdy. Pokuste se prozkoumat závislost této celkové hmotnosti na $ρ(0)$ a odhadnout její horní mez. Srovnejte váš výsledek s horní mezí hmotnosti bílého trpaslíka, kterou najdete v literatuře nebo na internetu. Uvažujte, že je hvězda tvořena héliem.
Zadali autoři seriálu Marek Pechal a Lukáš Stříteský.