Vyhledávání úloh podle oboru
Databáze úloh FYKOSu odjakživa
astrofyzika (85)biofyzika (18)chemie (24)elektrické pole (71)elektrický proud (76)gravitační pole (81)hydromechanika (146)jaderná fyzika (44)kmitání (57)kvantová fyzika (31)magnetické pole (43)matematika (89)mechanika hmotného bodu (298)mechanika plynů (87)mechanika tuhého tělesa (221)molekulová fyzika (72)geometrická optika (78)vlnová optika (65)ostatní (167)relativistická fyzika (37)statistická fyzika (21)termodynamika (155)vlnění (51)
hydromechanika
(5 bodů)5. Série 28. Ročníku - P. vycákaná
Bylo by možné plavat v bazénu, kdyby se voda v něm chovala jako dokonale nestlačitelná kapalina, jejíž viskozita se limitně blíží nule? Jak by se pohyb plavce odlišoval od plavání v běžné vodě? Co by se dělo s energií soustavy plavec a bazén v případě, že voda z bazénu může vytékat přes okraj? Na počátku je hladina vody zarovnaná s okrajem.
Fyzikální chemik plave.
(2 body)3. Série 28. Ročníku - 1. těžký vzduch
Jakou hmotnost má zemská atmosféra? Jakou část hmotnosti Země tvoří? Pro potřeby výpočtu znáte pouze hmotnost Země $M_{Z}$ a poloměr $R_{Z}$ Země, gravitační zrychlení $a_{g}$ na povrchu Země, hustotu vody $ρ$ a víte, že blízko povrchu Země v hloubce $h_{1}=10\;\mathrm{m}$ má hydrostatický tlak hodnotu zhruba jedné atmosféry $p_{a}=10^{5}\, \jd{Pa}$.
Nápověda: Jedná se o jednoduchou úlohu. Nejde nám o dokonale přesné řešení, ale o kvalifikovaný odhad podložený výpočtem.
Karel viděl zajímavou miskoncepci, podle níž je na Měsíci člověk lehčí jenom kvůli tomu, že je Měsíc menší. (A co kdyby byl hustší?)
(2 body)1. Série 28. Ročníku - 2. proudivé proudnice
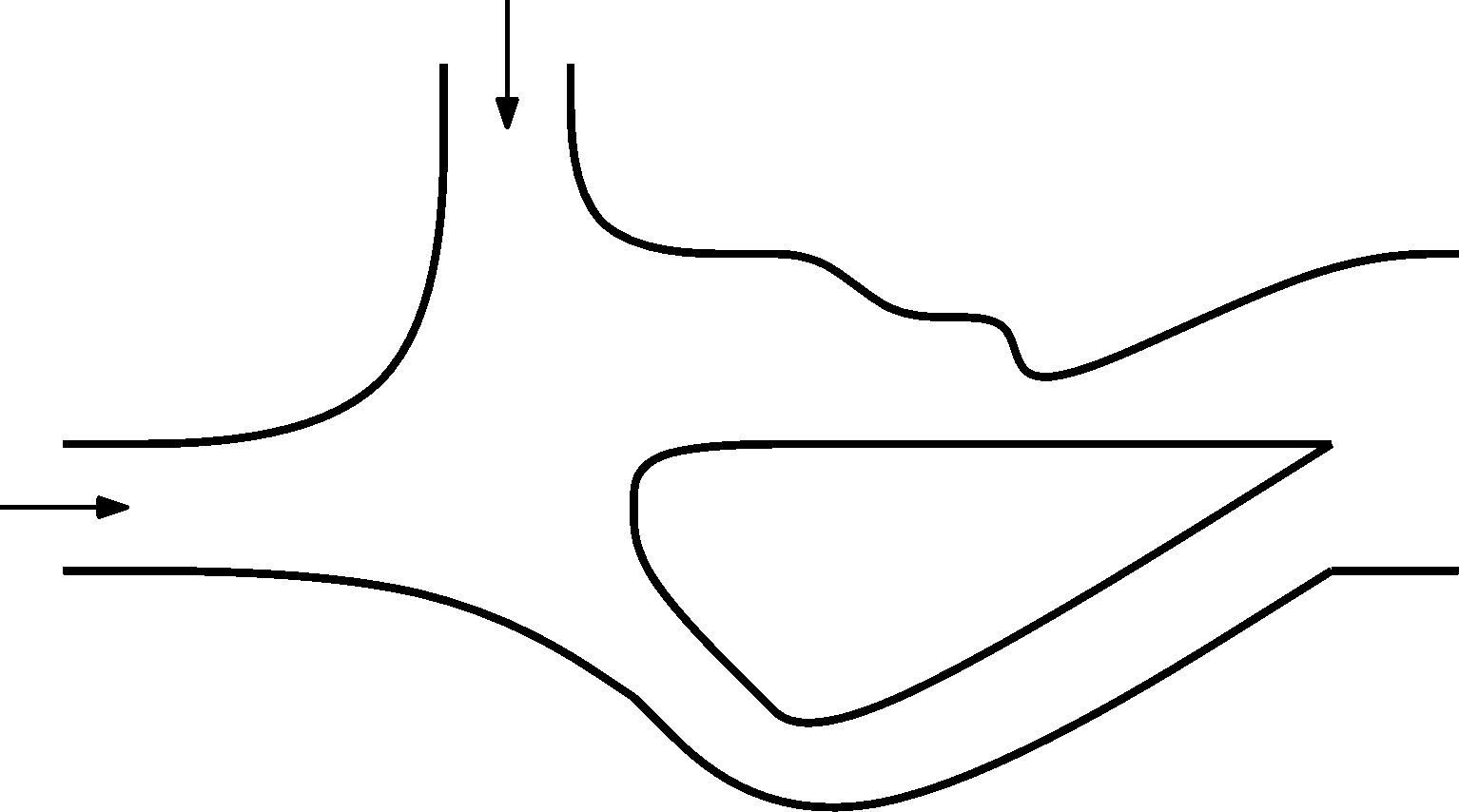
Nakreslete do obrázku proudnice. Do obou otvorů s šipkou vtéká stejné množství vody, všechna voda pak vytéká jediným, třetím otvorem. Proudění je ustálené a probíhá dostatečně pomalu, abychom ho mohli považovat za nevířivé. Při kreslení dbejte na pravidla, jimiž se tvar proudnic řídí a tato pravidla napište jako komentář k obrázku. Neočekáváme, že bude problém spočítán.
Poznámka: Kreslete do většího obrázku dostupného z webu.
kolar
(3 body)1. Série 28. Ročníku - 3. zrychlujeme
Vysvětlete, proč a jak se odehrají následující situace:
- V cisterně tvaru kvádru s vodou plove na hladině míček. Popište pohyb míčku, začne-li se cisterna rozjíždět s konstantním zrychlením dostatečně malým, aby voda nepřetekla přes okraj.
- V cisterně tvaru kvádru naplněné vodou se vznáší balonek naplněný vodou. Popište pohyb balonku, začne-li se cisterna rozjíždět s konstantním zrychlením dostatečně malým, aby voda nepřetekla přes okraj.
- V uzavřeném autobusu se vznáší u stropu balonek. Popište jeho pohyb, začne-li se autobus rozjíždět s konstantním zrychlením.
Dominika a Pikoš na zkoušce z fyziky.
(4 body)1. Série 28. Ročníku - 4. zkáza Titaniku
Náry si vždy přál mít loďku, a tak si jednoho krásného dne pořídil jednu ve tvaru kvádru bez horní podstavy (jako vana) s vnějšími rozměry $a$, $b$, $c$ a tloušťkou stěny $d$, která byla vyrobena z voňavého dřeva o hustotě $ρ$ (větší než hustota vody). Druhého krásného dne loďku spustil na vodu, ale zjistil, že má na dně dírku, kterou voda přitéká s průtokem $Q_{1}$. To bylo nemilé, a protože je mužem činu, začal počítat, za jak dlouho se mu do loďky začne valit voda vrchem. Stejnou otázku klade i tato úloha. Zvažte i situaci, kdy by Náry o hmotnosti $m$ v loďce seděl a mezi výpočty zoufale vyléval vodu svou botou s průtokem $Q_{2}$. Loďka je celou dobu vodorovně.
Kiki zaslechla o problému s tím, že skoro všechny úlohy vymýšlí Karel.
(2 body)5. Série 27. Ročníku - 1. natlakovaná žirafa
Porovnejte krevní tlak v hlavě dospělé žirafy a dospělého člověka. Systolický tlak na úrovni srdce je u člověka $p_{h1}=120\;\mathrm{mm}Hg$ a u žirafy $p_{g1}=280\;\mathrm{mm}Hg$, hustota krve obou živočichů je $ρ=1050\;\mathrm{kg\cdot m^{-3}}$. Uvažujte pouze případ, kdy člověk i žirafa stojí. Rychlost proudění krve v těle považujte za konstantní.
Mirek přemýšlel, proč žirafa neomdlí.
(2 body)4. Série 27. Ročníku - 2. zkumavky
Zkumavky o objemu $3\, \jd{ml}$ a $5\, \jd{ml}$ jsou spojeny krátkou tenkou trubičkou, v níž je pórovitá tepelně nevodivá přepážka, která umožňuje dosažení tlakové rovnováhy v systému. Obě zkumavky původně obsahují kyslík při tlaku $101,25\, \jd{kPa}$ a teplotě $20\, \jd{°C}$. První zkumavku ($3\, \jd{ml}$) ponoříme do nádoby s rovnovážnou soustavou ledu a vody a druhou ($5\, \jd{ml}$) do nádoby s párou. Jaký bude tlak v soustavě obou zkumavek po dosáhnutí mechanické rovnováhy? Jakého tlaku by se dosáhlo, pokud by ve zkumavkách byl za stejných podmínek dusík místo kyslíku?
Kiki vyhrabala něco z fyzikální chemie.
(2 body)3. Série 27. Ročníku - 2. Středozemní moře
Jak rychle v průměru teče voda Gibraltarským průlivem, když umožňuje střídání přílivu a odlivu ve Středozemním moři? Potřebné údaje si najděte na internetu a nezapomeňte citovat!
Lukáš byl překvapen výškou přílivu.
(4 body)3. Série 27. Ročníku - 3. pohárkovo vanová
Vezměme prázdný válcový kelímek. Otočme ho dnem vzhůru a tlačme ho pod klidnou vodní hladinu. Jak vysoký bude vzduchový sloupec v kelímku v závislosti na jeho ponoření?
Karel se inspiroval tím, jak si dříve hrával s kelímkem ve vaně.
(4 body)3. Série 27. Ročníku - 4. Ani k stáru, ani k stáru...
Balón i s košem má hmotnost $M$. Koš balónu se ponoří do přehrady a nateče do něj voda. Nyní trochu přitopíme a zvýšíme vztlak balónu na $Mg+F$. Koš má tvar hranolu se čtvercovou podstavou o hraně $a$ a je ponořený do hloubky $H$. Otvory v koši tvoří $p≪1$ z celkové plochy koše, o kterém předpokládáme, že je prázdný (kromě vody). Zanedbejme viskozitu vody a vlastní objem koše. Jak rychle se bude koš vynořovat v závislosti na hloubce ponoření?
Bonus: Za jak dlouho se vynoří?
Nápověda: Střední rychlost výtoku vody z části koše nad hladinou je rovna 2/3 maximální rychlosti výtoku.
Napadla Lukáše při sledování filmu Vratné lahve.