Vyhledávání úloh podle oboru

Kolik nejméně dětí by muselo roztočit svůj fidget spinner, aby se tak den na Zemi prodloužil o $1 \mathrm{ms}$? Všechny neznámé veličiny odhadněte.

Změřte délkovou hustotu struny, která vám měla přijít poštou společně se zadáním. Strunu ale nesmíte vážit.

Nápověda: Zkuste strunu rozkmitat.

Propisku (tuhou tyč) upustíme na stůl tak, že během svého letu svírá úhel $\alpha $ s vodorovnou rovinou. Jakou rychlostí dopadne její druhý konec (ten, co se stolu dotkne jako druhý), jestliže jsme těžiště upustili z výšky $h$? Všechny srážky jsou nepružné a tření mezi stolem a koncem propisky dostatečně velké.

Bonus: Spočítejte, jaký musíme zvolit úhel $\alpha$, aby druhý konec dopadl s co nejvyšší rychlostí. Pro jaké výšky se vyplatí propisku naklonit?

Máme homogenní úhelník ve tvaru L o stranách délek $b,c$. Je volně zavěšen v železničním vagóně za konec jedné strany tak, že jeho vrchol míří ve směru jízdy vagonu. S jakým zrychlením $a$ se musí vagon pohybovat, aby spodní strana úhelníku byla rovnoběžná se směrem jízdy? Relativistické jevy neuvažujte.

Bonus: Relativistické jevy uvažujte.

Změřte průhyb špejle položené na jejích koncích v závislosti na síle působící na jejím středu (viz obrázek).

Elza ráda cestuje vlakem. Při tom si všimla, že ihned po zastavení vlak mírně cukne dozadu. Elza nemá tušení, proč tomu tak je, pomozte jí to tedy objasnit. Uvažujte vlak s lokomotivou (hmotnost $m_r = \mathrm{82 t}$) a čtrnácti vagóny (hmotnost každého z nich je $m_v = \mathrm{48 t}$). Lokomotiva má brzdící váhu $p_r = \mathrm{113 t}$ a každý z vagónů má $p_v = \mathrm{99 t}$.$^1$ Dále uvažujme, že po zabrzdění se brzdící impulz šíří s konstantní rychlostí od lokomotivy na konec vlaku, přičemž poslední vagón začne brzdit za čas $\Delta t = \mathrm{12 s}$ po mašině.

Pro úplnost uvažujme, že spřáhla vozů jsou z části volná a umožňují pohyb. Sílu, kterou působí, můžeme v závislosti na výchylce $x$ popsat jako $x < 0 \Rightarrow F = -x k  ,$

$x = 0 \Rightarrow F = 0  ,$

$x > 0 \Rightarrow F = A \mathrm{sgn} \(x - x_v\)  ,$

kde kladný směr je tehdy, pokud se vozy od sebe vzdalují. Dále $k$ je tuhost nárazníku, $x_v$ je nezáporná konstanta a $A$ je tuhost spřáhla, přičemž $A \gg k$.

1. Analyticky vyšetřete průběh brzdění vlaku.
2. Najděte vlastní frekvenci kmitů pro $n$-tý vagón.
3. Najděte parametry $k$, $A$ a $x_v$ tak, aby kmitání vozů bylo vzhledem k brzdění kriticky tlumené.
4. Splňuje tento model to, co Elza pozorovala? Udělejte Elze radost a najděte lepší model chování vlaku.
5. Numericky řešte tento nový model.

Bonus: Řešte případ, ve kterém bude jeden z vozů vypojený, tedy nebude brzdit.

1.) Brzdící váha označuje poměrnou schopnost vozidla brzdit. Je to absolutní jednotka a můžeme jí lineárně přeškálovat na brzdící sílu.

Mirek by rád zastřelil potkana, kterého vídá na kolejích. Připravil si tedy jednoduchou vzduchovou pušku, kterou si můžeme modelovat jako trubku s konstantním průřezem $S=15\;\mathrm{mm}$ a délkou $l=30\;\mathrm{cm}$, která je na jedné straně uzavřená a na druhé otevřená. Do ní se chystá Mirek umístit náboj hmotnosti $m=2\;\mathrm{g}$, který trubku akorát utěsní, a to ve vzdálenosti $d=3\;\mathrm{cm}$ od uzavřeného konce. Náboj zde zatím nechá upevněný v klidu a natlakuje uzavřenou část trubky na určitý tlak $p_{0}$. Posléze náboj uvolní. Chce aby na konci ústí byla minimálně rychlost náboje $v=90\;\mathrm{m}\cdot \mathrm{s}^{-1}$. Poraďte mu, na jaký tlak by musel vzduchovou pušku natlakovat, aby náboj vyšel s takovou rychlostí, pokud by plyn byl ideální, a diskutujte realističnost uspořádání. Předpokládejte, že náboj je uvolňován kvazistatickým adiabatickým dějem, kde $κ=7/5$, protože se jedná o dvouatomový plyn. Uvažujte, že z vnějšku působí na náboj atmosférický tlak $p_{a}=10^{5}\;\mathrm{Pa}$. Zanedbejte energetické ztráty vyvolané třením, odporem vzduchu a stlačováním plynu před nábojem.

Máme homogenní tyč konstantního průřezu délky $l$ připevněnou na jednom konci k otočnému kloubu. Na počátku směřuje tyč přímo vzhůru a jsme v homogenním tíhovém poli se zrychlením o velikosti $g$. Tyč se vlivem mírného závanu větru začne otáčet a „padat“ dolů, ale stále je držena otočným kloubem. S jakým zrychlením se bude pohybovat konec tyče v průběhu času?

Představte si situaci, kdy máme 3 stejné nerotující disky, které se pohybují přesně v jedné přímce v pořadí 1, 2, 3. Všechny tři se pohybují bez tření a dalších odporových sil po vodorovné podložce, přičemž disky 1 a 2 jedou doprava a proti nim jede disk 3 doleva. Platí, že rychlost 1 je větší než 2. Jak závisí výsledné rychlosti disků po proběhnutí všech srážek na pořadí srážek? A jaké tyto rychlosti budou? Srážky probíhají pružně. (Jako vždy nezapomeňte, že odpověď je potřeba řádně zdůvodnit.)

Bonus: Disky mají různou hmotnost.

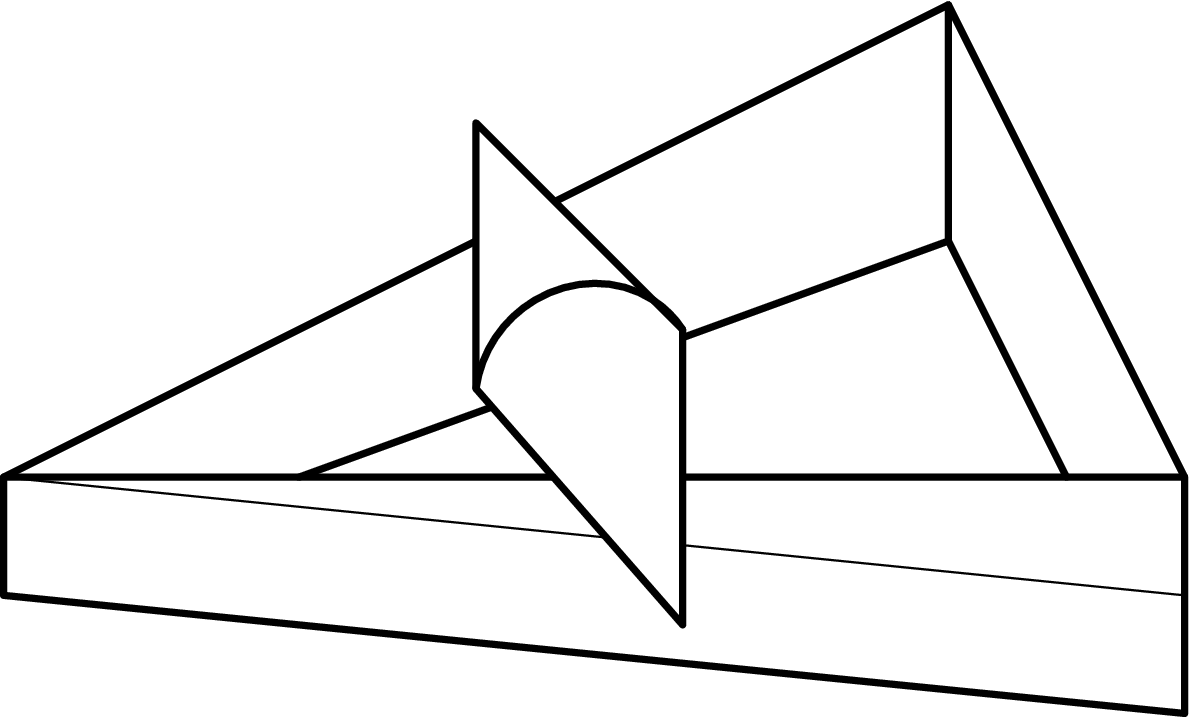
Mějme dřevěnou konstrukci, která má půdorys rovnoramenného trojúhelníku a výška jejích dvou ramen roste směrem k základně s úhlem $α=2°$. Do vrcholu naproti základně $c=35\;\mathrm{cm}$, u nějž má trojúhelník úhel $β=70°$, umístíme dvojkužel s vrcholovým úhlem $φ=40°$ a výškou $2h=40\;\mathrm{cm}$. Kužel se samovolně začne valit „do kopce“, tedy ve směru růstu hran trojúhelníku.

• Vysvětlete, proč se dvojkužel může kutálet do kopce.
• Jak závisí poloha těžiště kuželu na uražené vzdálenosti?
• Jaká je rychlost kužele těsně před nárazem na základnu?
• Kolik otáček kužel vykoná během své cesty?

Na počátku je kužel umístěn horizontálně na konstrukci tak, že jeho těžiště se nachází přesně nad vrcholem trojúhelníku proti základně.