Vyhledávání úloh podle oboru
Databáze úloh FYKOSu odjakživa
astrofyzika (85)biofyzika (18)chemie (24)elektrické pole (71)elektrický proud (76)gravitační pole (81)hydromechanika (146)jaderná fyzika (44)kmitání (57)kvantová fyzika (31)magnetické pole (43)matematika (89)mechanika hmotného bodu (298)mechanika plynů (87)mechanika tuhého tělesa (221)molekulová fyzika (72)geometrická optika (78)vlnová optika (65)ostatní (167)relativistická fyzika (37)statistická fyzika (21)termodynamika (155)vlnění (51)
vlnění
3. Série 10. Ročníku - 2. dopravní přestupek
Jede si tak jednou pan Doppler po městě a co nevidí. Zastavuje ho vozidlo policie a příslušník povídá: „Pane řidiči, jste si vědom toho, že jste jel na červenou?“
„Nikoliv. Když jsem projížděl kolem semaforu, tak jsem viděl zelenou. Tím jsem si naprosto jist, odvětil pan Doppler.“
„Tak v tom případě vám musím dát pokutu za rychlou jízdu!“
Kolik zaplatil pan Doppler a proč, jsou-li sazby 1 Kč za $1\; \textrm{km}\cdot h^{-1}$ přes povolený limit $60\; \textrm{km}\cdot h^{-1}$ ve městě?
4. Série 9. Ročníku - 1. Pozor, přímý přenos!
Ve velké newyorské koncertní síni Carnegie Hall sedí malý český človíček Honzíček, na programu je Beethovenova sedmá symfonie. Ne každý milovník vážné hudby z naší zemičky má na to, aby slyšel takovýto koncert na vlastní uši, a tak jiný malý český človíček Pepíček (mimochodem blízký přítel našeho hrdiny) sedí hezky doma v Praze na Vinohradech ve svém křesílku s ouškem přitisknutým na rozhlasovém přijímači. Do jaké řady má Honzíček koupený lístek, víte-li, že spolu se svým přítelem Pepíčkem slyší tóny Sedmé ve stejný okamžik?
Pozn.: Pokud postrádáte některé údaje, tak si je vyhledejte; jestli něco nemůžete skutečně zjistit, např. vzdálenost řad v C. Hall, tak si to odhadněte, jsme přece fyzici, ne?
3. Série 9. Ročníku - 2. dálkový průzkum
Zjistit přesné údaje o Merkuru bylo pro astronomy vždy velkým problémem. Není jednoduché změřit pomocí dalekohledu jeho zdánlivý průměr, který nepřesahuje $13''$ a protože na povrchu Merkuru není vidět mnoho podrobností, zůstavala rychlost jeho rotace dlouho neznámá. Od konce minulého století se předpokládalo, že Merkur má takzvanou vázanou rotaci, to znamená, že jedna jeho otočka kolem osy je stejně dlouhá jako doba oběhu kolem Slunce, tedy 88 dní. Tento omyl vyvrátilo teprve v 60. letech radarové pozorování. Dejme tomu, že radioastronomové vyslali v čase $t_{0}=0\;\mathrm{s}$ signál směrem k Merkuru a jeho odraz pozorují od doby $t_{1}=1\,070{,}156\,24\;\mathrm{s}$ do $t_{2}=1\,070{,}188\,79\;\mathrm{s}$. Při dalším měření se soustředili na rudý posuv přijaté vlny. Původní signál měl frekvenci $100\;\textrm{MHz}$ a frekvence jednotlivých složek ozvěny se pohybovala od $f_{1}=99{,}977\,397\,00\;\mathrm{MHz}$ do $f_{2}=99{,}977\,405\,06\;\mathrm{MHz}$. Vypočtěte z těchto údajů (za předpokladu, že sklon rotační osy této planety vůči ekliptice je malý) vzdálenost a rychlost vzdalování Merkuru od observatoře, jeho poloměr, úhlovou rychlost rotace a dobu jedné otočky kolem osy.
6. Série 8. Ročníku - 3. před plechem, za plechem
K oblíbeným položkám v matfyzáckém folkloru patří tento zvyk. Zahlédne-li takové indiviuum dlouhou stěnu z vlnitého plechu (nebo jiného podobně tvarovaného materiálu), postaví se cca. $5\; \textrm{m}$ od ní a silně dupne. Ozve se (kromě obvyklého plesknutí) delší drnčivý zvuk, který postupně mění svou výšku.
Vysvětlete, jak tento zvuk vzniká, a spočtěte, jak se mění jeho frekvence s časem. Jaká je doba, po kterou ji slyší? Tvarování plechu je ukázáno na obrázku.
3. Série 8. Ročníku - 2. kostka
Nalezněte tvar čela vlny na hladině rybníka, do něhož jsme vhodili pravidelný hexaedr (tj. šestistěn, pro neznalé krychle) o hraně $a$ tak, že dopadla na hladinu jednou svou stěnou. Jak bude tato vlnoplocha vypadat ve vzdálenosti $r\gg a$?
4. Série 2. Ročníku - 3. reflektor
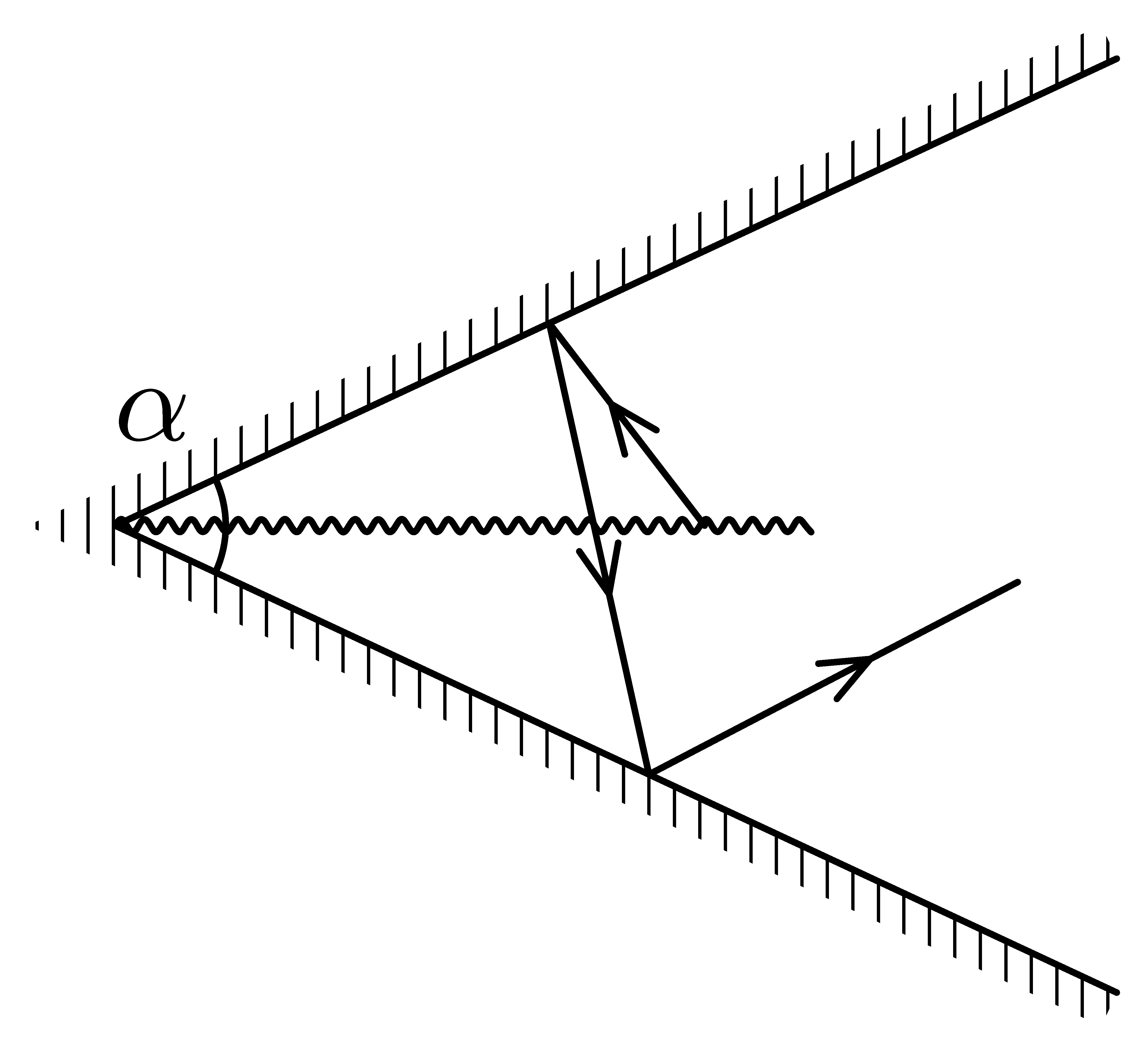
Reflektor
Jaký musí být vrcholový úhel kuželového reflektoru, aby se paprsky ze svítícího vlákna v ose kuželu délky $l$ odrazily o stínítko jednou, dvakrát, $n$-krát? Stínítko je dostatečně velké.
3. Série 2. Ročníku - 4. jak hluboká je studna?
Hloubku studny chceme určit s relativní chybou $2\; \%$ tak, že do ní pustíme kámen a měříme dobu, za kterou uslyšíme pád kamene na dno od jeho vypuštění. Při jaké hloubce studny už musíme uvažovat rychlost šíření zvuku?
3. Série 2. Ročníku - E. index lomu
Určete co nejpřesněji index lomu přiloženého plátku umělé hmoty. Uveďte postup a odhadněte přesnost provedeného měření.
2. Série 1. Ročníku - 2. čluny

Pohled na čluny
Obrázek ukazuje dva čluny pohybující se po hladině jezera. Z obálky vln soudíme, že
- obě lodi plují větší rychlostí, než je rychlost povrchových vln, přičemž loď I pluje rychleji než loď II
- loď I pluje rychleji než loď II, ale nemusí nutně plout větší rychlostí, než je rychlost povrchových vln
- ani a), ani b)
1. Série 1. Ročníku - 3. klavír
Předpokládejte, že vlastníte výborný koncertní klavír. Chcete ho nechat naladit. Pozvete nejlepšího ladiče pian. Ten ladí klavír tak, že porovnává zvuk klavíru a etalonu (ladičky). Jak dlouho mu bude trvat perfektní naladění klavíru?
- zhruba hodinu
- zhruba den
- zhruba týden
- zhruba měsíc
- nekonečně dlouho