Vyhledávání úloh podle oboru

Mějme nekonečný drát stočený do pravotočivé šroubovice (helixu). Drát je rovnoměrně nabitý a osa helixu je totožná s osou $z$. Do vzniklého pole pošleme nabitou částici (drát je tenký, takže do něj částice nenarazí). V jistém časovém okamžiku známe její $p_{z}$ a $L_{z}$, tedy $z$ové komponenty hybnosti a momentu hybnosti. Můžeme v jiném okamžiku určit $p_{z}$, známe-li v tomto okamžiku $L_{z}?$

(Problém lze vyřešit zcela exaktně. Naproti tomu není určitě nezajímavé zkusit situaci počítačově simulovat a dostat tak hledanou závislost v podstatě experimentálně, v případě ověřit teoretickou předpověď.)

Do kapalného dielektrika jsou svisle ponořeny dvě čtvercové paralelní vodivé desky o straně $a$. Nejsou-li desky nabity, vystoupí hladina mezi deskami do výšky $h_{0}$ (měřeno od dolního okraje desek). O jakou vzdálenost $\Delta h$ se zvýší hladina kapaliny mezi deskami, nabijeme-li desky na napětí $U$? Permitivita kapaliny je $\epsilon$, hustota $\rho$ a vzdálenost desek je $d$ ($d << a$).

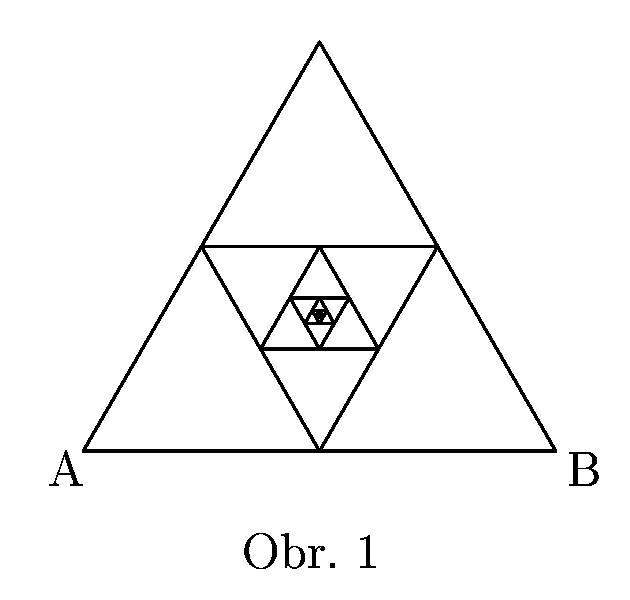
Mějme drát, jehož jednotka délky má odpor $R$. Z rovnostranných trojúhelníků z něj vyrobených postavíme nekonečnou síť naznačenou na obrázku (nejdelší strana má jednotkovou délku). Jaký odpor bude mezi vrcholy největšího trojúhelníku?

Uvažujte tranzistor JFET vyrobený z polovodiče typu N ve tvaru kvádru o hranách $a$, $b$, $c$. Na dvou protilehlých stěnách jsou vývody S a D, na jiných dvou protilehlých je z polovodiče typu P vývod G (obě stěny jsou vodivě propojeny na jeden vývod). Předpokládejme, že šířka přechodu je dána vztahem $d=d_{0}+λU'$, kde $U'$ je závěrné napětí. Předpokládejme navíc, že proud může procházet pouze oblastí polovodiče N mimo přechod. Proud tekoucí polovodičem se stanoví ze vztahu $I=SσU⁄l$, kde $U$ je napětí mezi svorkami na polovodiči s vodivostí $σ$, jejichž vzdálenost je $l$ a proud prochází kolmo plochou $S$. Z tohoto jednoduchého modelu se pokuste stanovit závislost proudu tranzistorem na napětí mezi svorkami S a D, jako parametr uvažujte napětí na svorce G. Úlohu si ještě můžete zpestřit porovnáním výsledku s charakteristikou válcového tranzistoru JFET, kde je polovodič P po celém plášti válce.

Proveďte diskusi funkce PNP tranzistoru. Porovnejte s funkcí NPN tranzistoru kvalitativně, ale i kvantitativně. Díra má stejný náboj jako elektron, má však menší pohyblivost. Co se stane, když posvítíme dovnitř tranzistoru (PNP i NPN)?

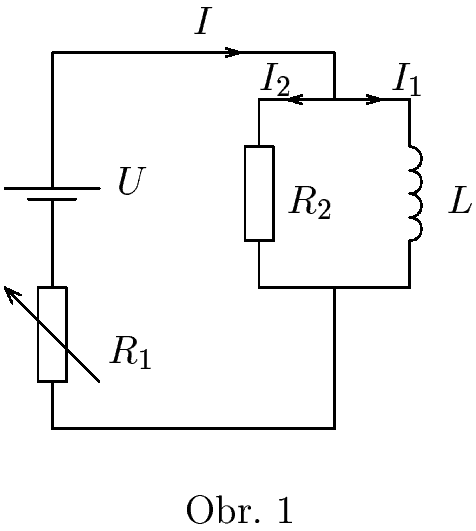
Mějme následující obvod (viz. obrázek). Část obvodu obsahující $R_{2}$ a $L$ $(10\,\jd{H})$je ponořena do kapalného hélia. Vodiče v této části jsou supravodivé (mají nulový odpor). Vyndáme-li $R_{2}$ z hélia, má odpor $5 \,\jd{Ω}$.

První experiment probíhá následovně: Proud $I$ měníme pomocí $R_{1}$ tak, aby v časovém intervalu $(t_{0},t_{1})$ byl konstantní $1 \,\jd{A}$, v $(t_{1},t_{2})$ rovnoměrně klesal na nulu, v $(t_{2},t_{3})$ rovnoměrně stoupal na $0,5 \,\jd{A}$ a dále byl konstantní. V čase $t_{3}$ rezistor $R_{2}$ vyndáme z hélia a v čase $t_{4}$ jej tam opět spustíme. V $t_{0}$ je $I_{1}=I_{2}=0,5 \,\jd{A}$. Určete časový průběh $I_{1}$ a $I_{2}$ v časovém intervalu ($t_{0},t_{4})$.

Druhý experiment probíhá následovně: Na počátku je $R_{2}=0 \,\jd{Ω}$, $I_{1}=0 \,\jd{A}$, $R_{1}=7,5 \,\jd{Ω}$, $I=0,5 \,\jd{A}$. $R_{1}$ se dále nemění. V čase $t_{1}$ vyndáme $R_{2}$ z hélia a v čase $t_{2}$ jej tam opět spustíme. Načrtněte do grafu průběh časové závislosti $I$, $I_{1}$, $I_{2}$.

Uvažte měděný kruhový závit o poloměru $R=10\;\mathrm{cm}$, který leží na stole v magnetickém poli Země (vektor magnetické indukce je rovnoběžný se stolem, který se nachází na rovníku). Poloměr drátu je $r=0,3\;\mathrm{mm}$. Závitem prochází proud $I$. Určete $I$ tak, aby se závit překlopil (předpokládejte, že tření je dostatečně velké, takže závit neproklouzne).

Uvažujme reálnou křemíkovou diodu s přechodovým napětím $0,6 \,\jd{V}$ při pokojové teplotě (fyzici pro jednoduchost považují za pokojovou teplotu $300 \,\jd{K}$, oproti normální $20{^\circ} \,\jd{C} = 293 \,\jd{K}$, protože se s tím lépe počítá a lépe se to pamatuje). Pokuste se z uvedených rovnic (i v minulých dílech seriálu) odhadnout, jak se bude dioda chovat při zvýšení teploty o $10 \,\jd{K}$, $20 \,\jd{K}$ a $40 \,\jd{K}$. Není třeba do puntíku počítat, co se přesně stane, jde pouze o kvalitativní odhady. Ti, kdo mají možnost, mohou odhady ověřit měřením – k měření voltampérové charakteristiky je třeba pouze dioda, ochranný odpor (nikdy nezapojujte diodu v propustném směru přímo na napětí!), zdroj napětí, voltmetr a ampérmetr. Odhady by měly být pro přehlednost aspoň schematicky nakreslené v nějakém grafu. Zaměřte se zejména na velikost závěrného proudu a polohu kolena v propustném směru.

Rezonanční obvod se skládá z neideální cívky s indukčností $L=1\,\jd{ H}$ a vnitřním odporem $R=1\,\jd {Ω}$ a neideálního kondenzátoru s kapacitou $C=1\,\jd{µF}$ o neznámém svodovém odporu $R_{x}$. Jaká je velikost $R_{x}$, pokud víme, že se 1/3 původní energie rezonančního obvodu ztrácí v podobě tepla na odporu cívky?

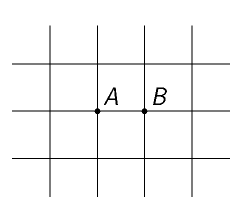
Spočtěte elektrický odpor $R$ mezi body $A$ a $B$ nekonečně rozlehlé čtvercové sítě (viz obr. 1). Jednotlivé úsečky tvořící síť mají odpor $R_{0}$.